Areas of Segments (radians)

Quick Recap

We now know that the area of a circle is $\pi r^2$πr2. We also now know that the area of a sector is some fraction of that full area $\frac{\theta}{2\pi}\times\pi r^2=\frac{1}{2}r^2\theta$θ2π​×πr2=12​r2θ. The fraction is the proportion of $2\pi$2π that the sector's angle at the centre takes up.

Recall that there is a minor sector and a major sector associated with any given angle at the centre. The other sector can simply be found by using $2\pi-\theta$2π−θ in the formula for the area of a sector.

$Area=\pi r^2$Area=πr2

$Area=\frac{1}{2}r^2\theta$Area=12​r2θ	$Area=\frac{1}{2}r^2\left(2\pi-\theta\right)$Area=12​r2(2π−θ)
$Area=\frac{1}{2}r^2\left(2\pi-\theta\right)$Area=12​r2(2π−θ)	$Area=\frac{1}{2}r^2\theta$Area=12​r2θ

Area of a Minor Segment

What about the area of a segment? Remember that a segment is the region bounded by a chord and the arc subtended by the chord (a chord is an interval connecting two points on a circle).

This may seem very difficult to do, until we realise that the area of a minor segment is just the area of a sector minus the area of a triangle.

$\frac{1}{2}r^2\theta$12​r2θ		$\frac{1}{2}r^2\sin\theta$12​r2sinθ		$\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta$12​r2θ−12​r2sinθ

Here we got the area $\frac{1}{2}r^2\sin\theta$12​r2sinθ of the triangle from our formula $Area=\frac{1}{2}ab\sin C$Area=12​absinC.

Area of a Major Segment

How do we find the area of a major segment? In fact, the formula above will still hold. Let's see why.

The area of a major segment is just the area of the major sector, which subtends angle $\theta$θ, plus the area of a triangle with angle $2\pi-\theta$2π−θ.

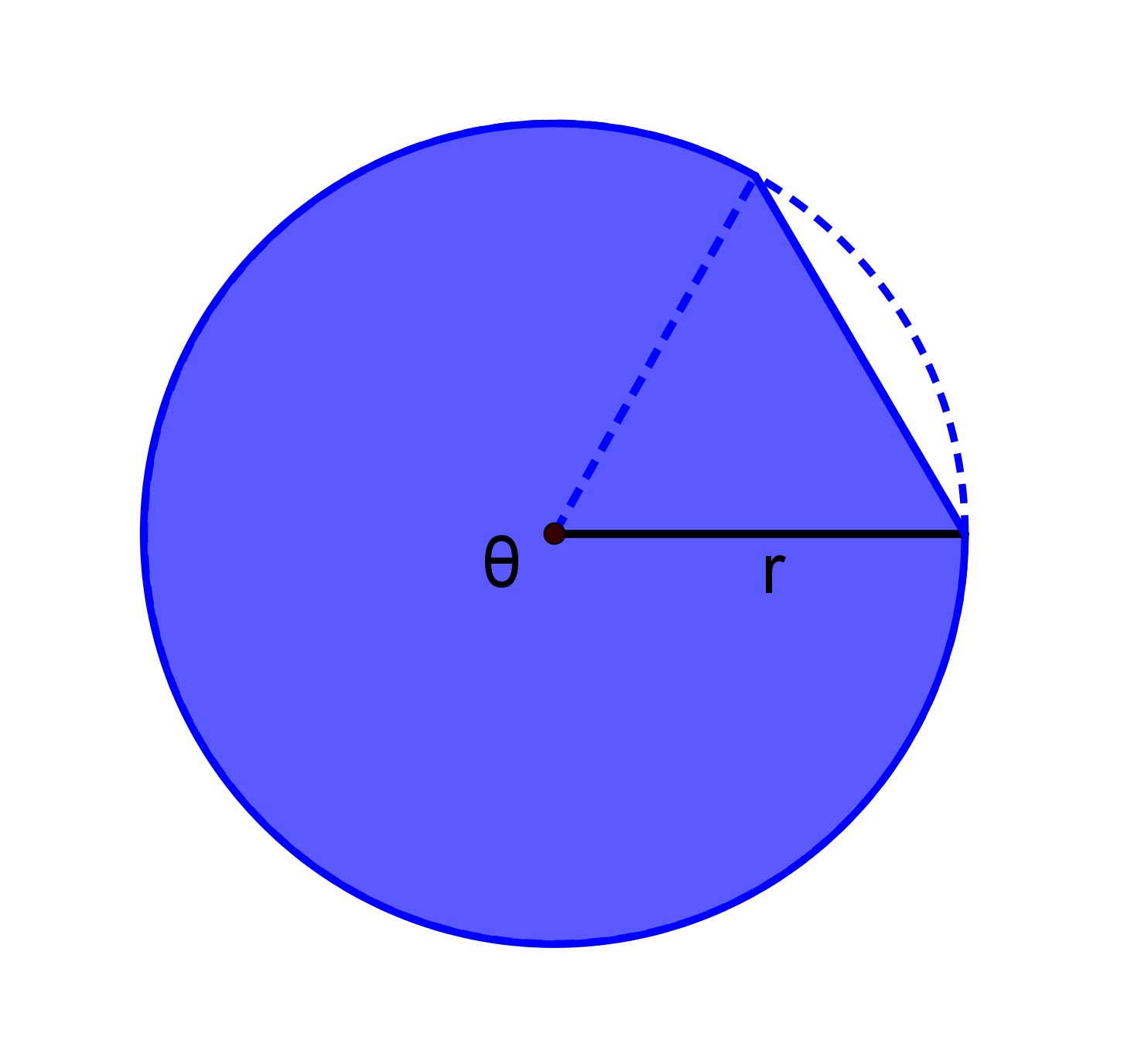$\frac{1}{2}r^2\theta$12​r2θ		$\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2sin(2π−θ)		$\frac{1}{2}r^2\theta+\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2θ+12​r2sin(2π−θ)

However, since $\sin\left(2\pi-\theta\right)=-\sin\theta$sin(2π−θ)=−sinθ, from the symmetry of the sine function, this is the same as our original formula:

$\text{Area of segment}$Area of segment	$=$=	$\frac{1}{2}r^2\theta+\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2θ+12​r2sin(2π−θ)
	$=$=	$\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta$12​r2θ−12​r2sinθ
	$=$=	$\frac{1}{2}r^2\left(\theta-\sin\theta\right)$12​r2(θ−sinθ)

Hence, no matter what $\theta$θ is, we can use this formula to figure out the area of the segment that subtends $\theta$θ.

 

Alternatively, if we have already calculated the area of the minor segment we can subtract this from the area of the circle to find the area of the corresponding major segment.

$\pi r^2$πr2		$\frac{1}{2}r^2\left(\theta-\sin\theta\right)$12​r2(θ−sinθ)		$\pi r^2-\frac{1}{2}r^2\left(\theta-\sin\theta\right)$πr2−12​r2(θ−sinθ)

Examples

Question 1

Question 2

Question 3