Trigonometry and Similarity

Lesson

Practice

Lesson

We we looked at similar triangles, we learnt that all the sides in similar triangles are in the same ratio. So, when we find the ratio of two sides in a triangle, the ratio of the corresponding sides in a similar triangle will always be the same.

As such, this means that the trigonometric ratios (sine, cosine and tangent) in similar right-angle triangles are always equal. Let's consider the two right-angled triangles below.

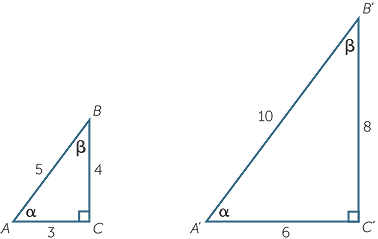
In triangle ABC:

$\sin\alpha$`sinα`	$=$=	$\frac{4}{5}$45	$\sin\beta$`sinβ`	$=$=	$\frac{3}{5}$35
$\cos\alpha$`cosα`	$=$=	$\frac{3}{5}$35	$\cos\beta$`cosβ`	$=$=	$\frac{4}{5}$45
$\tan\alpha$`tanα`	$=$=	$\frac{4}{3}$43	$\tan\beta$`tanβ`	$=$=	$\frac{3}{4}$34

In triangle A'B'C':

$\sin\alpha$`sinα`	$=$=	$\frac{8}{10}$810	$\sin\beta$`sinβ`	$=$=	$\frac{6}{10}$610
	$=$=	$\frac{4}{5}$45		$=$=	$\frac{3}{5}$35
$\cos\alpha$`cosα`	$=$=	$\frac{6}{10}$610	$\cos\beta$`cosβ`	$=$=	$\frac{8}{10}$810
	$=$=	$\frac{3}{5}$35		$=$=	$\frac{4}{5}$45
$\tan\alpha$`tanα`	$=$=	$\frac{8}{6}$86	$\tan\beta$`tanβ`	$=$=	$\frac{6}{8}$68
	$=$=	$\frac{4}{3}$43		$=$=	$\frac{3}{4}$34

As you can see, the ratios are the same in both triangles.

So once we can prove that two triangles are similar, we can find corresponding trigonometric ratio, as well as corresponding angles and side lengths.

Examples

Question 1

Two right-angled triangles are measured, and a pair of corresponding angles are found to have a sine ratio of $\frac{240}{250}$240250 and $\frac{24}{25}$2425 respectively.

Are the two triangles similar?
Yes
A
No
B

Question 2

Consider the given triangles.

Are the two triangles similar?
Yes
A
No
B
Which rule confirms similarity?
Two pairs of angles are equal.
A
The ratio of three pairs of corresponding sides is equal.
B
The ratio of two pairs of corresponding sides is equal, and the pair of included angles are also equal.
C

Outcomes

10.G.T.1

Definitions, examples, counterexamples of similar triangles, covering (a) If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio, (b) If a line divides two sides of a triangle in the same ratio, the line is parallel to the third side, (c) If in two triangles, the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar, (d) If the corresponding sides of two triangles are proportional, their corresponding angles are equal and the two triangles are similar (e) If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar.