
Find angles in right-angled triangles
We have already seen what the trigonometric ratios are:
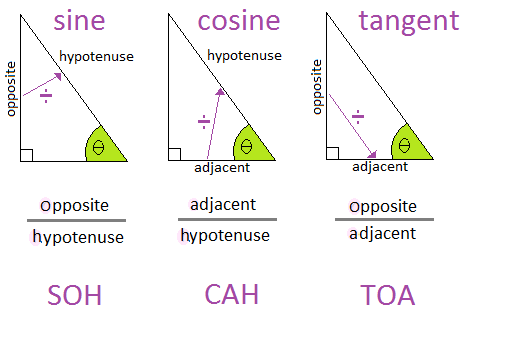
We know wow to calculate with them, and how to find the length of unknown sides of right-angled triangles with them.
We can also use the trigonometric ratios to find the size of unknown angles. To do this we need any 2 of the side lengths.
- label the sides as O, A or H with respect to the position of the angle you want to find
- identify the appropriate trigonometric ratio that applies [either sine (sin), cosine (cos) or tangent (tan)]
- using algebra, solve the equation for the angle, (write the rule, fill in what you know, then solve using inverse operations)
- reflect and check (do a quick check on your calculator to confirm your answer is correct)
Examples
Question 1

Find the angle indicated in this diagram.

1. label the sides as O, A or H with respect to the position of the angle
2. Identify the appropriate ratio that uses O and H. For this question it will be sine (sin)
3. Using algebra, solve the equation for the angle
(write the rule) $\sin\theta=\frac{O}{H}$sinθ=OH
(fill in what you know) $\sin\theta=\frac{5}{8}$sinθ=58
(solve using inverse operations) $\theta=\sin^{-1}\left(\frac{5}{8}\right)$θ=sin−1(58) use a calculator for this bit!
$\theta=38.68$θ=38.68°
Using the inverse operation for sin/cos/tan
We looked already at calculating angles from a value, here is a reminder.
Find $\theta$θ if $\sin\theta=0.65$sinθ=0.65 answer to $2$2 decimal places
This question is asking us what the angle is if the ratio of the opposite and hypotenuse is $0.65$0.65. To answer this question you use the inverse sin button on your scientific calculator. Often it looks a bit like this $\sin^{-1}$sin−1
$\sin\theta=0.65$sinθ=0.65
$\sin^{-1}$sin−1 $0.65=40.54$0.65=40.54°
Question 2
 Find the value of the angle indicated.
Find the value of the angle indicated.
We have the opposite and adjacent sides here, so the ratio I will use is tangent (tan).
$\tan\theta=\frac{O}{A}$tanθ=OA write the rule
$\tan\theta=\frac{14.77}{12.24}$tanθ=14.7712.24 fill in what we know
$\theta=\tan^{-1}\left(\frac{14.77}{12.24}\right)$θ=tan−1(14.7712.24) use inverse operations to rearrange, and then use a calculator
$\theta=50.35$θ=50.35°
Question 3
Find the value of $x$x to the nearest degree.

A right-angled triangle with vertices labeled A, B and C. Vertex A is at the top, B at the bottom right, and C at the bottom left. A small square at vertex A indicates that it is a right angle. Side interval(BC), which is the side opposite vertex A, is the hypotenuse and is marked with a length of 25. The angle located at vertex B is labelled x. Side interval(AB), descending from the right angle at vertex A to vertex B, is marked with a length of 7, and is adjacent to the angle x. Side interval(AC) is opposite the angle x.
Question 4
Consider the given figure.

Find the unknown angle $x$x, correct to two decimal places.
Find $y$y, correct to two decimal places.
Find $z$z correct to two decimal places.
Question 5
The person in the picture sights a pigeon above him. If the angle the person is looking at is $\theta$θ, find $\theta$θ in degrees.
Round your answer to two decimal places.
