Partial Fraction Decompositions
A very important skill to learn is the technique of breaking up an algebraic fraction into its component parts. It is akin to reversing the process of addition of fractions.
Explaining the concept
To motivate our discussion, suppose we wished to break up the fraction $\frac{5}{6}$56 into the sum of two fractions with prime denominators $2$2 and $3$3.
Put mathematically, we wish to find numbers $A$A and $B$B such that $\frac{5}{6}=\frac{A}{2}+\frac{B}{3}$56=A2+B3.
If we add the two fractions on the right hand side we have:
| $\frac{5}{6}$56 | $=$= | $\frac{A}{2}+\frac{B}{3}$A2+B3 |
| $\frac{5}{6}$56 | $=$= | $\frac{3A+2B}{6}$3A+2B6 |
Since the denominator $6$6 occurs in both fractions on each side of the last equation, we can say that the numerators of these fractions are equal as well. In other words we declare that $5=3A+2B$5=3A+2B, and this can be made true by choosing $A=B=1$A=B=1.
Hence we can write that $\frac{5}{6}=\frac{1}{2}+\frac{1}{3}$56=12+13.
We say that $\frac{1}{2}$12 and $\frac{1}{3}$13 are the partial fractions of $\frac{5}{6}$56.
Here are the values of $A$A and $B$B for other fractions with $6$6 as denominator:
| $\frac{1}{6}$16 | $\frac{2}{6}$26 | $\frac{3}{6}$36 | $\frac{4}{6}$46 | $\frac{5}{6}$56 | $\frac{6}{6}$66 |
|---|---|---|---|---|---|
| $A=1$A=1 | $A=0$A=0 | $A=1$A=1 | $A=0$A=0 | $A=1$A=1 | $A=2$A=2 |
| $B=-1$B=−1 | $B=1$B=1 | $B=0$B=0 | $B=2$B=2 | $B=1$B=1 | $B=0$B=0 |
| $\frac{1}{2}-\frac{1}{3}$12−13 | $\frac{0}{2}+\frac{1}{3}$02+13 | $\frac{1}{2}+\frac{0}{3}$12+03 | $\frac{0}{2}+\frac{2}{3}$02+23 | $\frac{1}{2}+\frac{1}{3}$12+13 | $\frac{2}{2}+\frac{0}{3}$22+03 |
Note that because $2$2 and $3$3 are prime, these values of $A$A and $B$B are unique for each fraction.
First algebraic example
In a similar way, an expression like $\frac{x}{\left(x-2\right)\left(x+1\right)}$x(x−2)(x+1) can be broken up into its partial fractions so that for constants $A$A and $B$B, $\frac{x}{\left(x-2\right)\left(x+1\right)}=\frac{A}{x-2}+\frac{B}{x+1}$x(x−2)(x+1)=Ax−2+Bx+1.
Using this example, the task is to find $A$A and $B$B and this is done in the same way as before.
| $\frac{x}{\left(x-2\right)\left(x+1\right)}$x(x−2)(x+1) | $=$= | $\frac{A}{x-2}+\frac{B}{x+1}$Ax−2+Bx+1 |
| $\frac{x}{\left(x-2\right)\left(x+1\right)}$x(x−2)(x+1) | $=$= | $\frac{A\left(x+1\right)+B\left(x-2\right)}{\left(x-2\right)\left(x+1\right)}$A(x+1)+B(x−2)(x−2)(x+1) |
| $\therefore$∴ $x$x | $=$= | $A\left(x+1\right)+B\left(x-2\right)$A(x+1)+B(x−2) |
| $x$x | $=$= | $Ax+A+Bx-2B$Ax+A+Bx−2B |
| $1x+0$1x+0 | $=$= | $\left(A+B\right)x+\left(A-2B\right)$(A+B)x+(A−2B) |
Equating coefficients reveals:
| $A+B$A+B | $=$= | $1$1 $(1)$(1) |
| $A-2B$A−2B | $=$= | $0$0 $(2)$(2) |
This is not hard to solve simultaneously. By subtracting $(2)$(2) from $(1)$(1), we have that $3B=1$3B=1 and thus $B=\frac{1}{3}$B=13. This means, from $(1)$(1), that $A=\frac{2}{3}$A=23, and so we can conclude that:
$x=\frac{\frac{2}{3}}{x-2}+\frac{\frac{1}{3}}{x+1}=\frac{2}{3\left(x-2\right)}+\frac{1}{3\left(x+1\right)}$x=23x−2+13x+1=23(x−2)+13(x+1).
General procedures
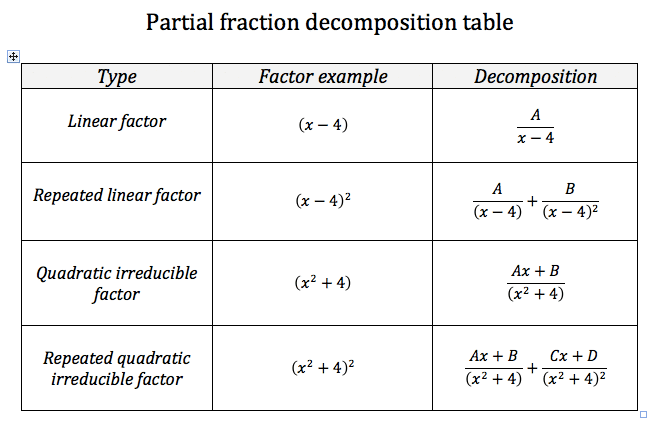
General procedures have been developed to break an algebraic fraction into its component parts. The table below summarises how denominator factors are treated.
Three important points need to be made:
- Before an algebraic fraction $\frac{P\left(x\right)}{Q\left(x\right)}$P(x)Q(x) is broken up into partial fractions, check that the degree of $P\left(x\right)$P(x) $\le$≤ the degree of $Q\left(x\right)$Q(x). If it isn't, then $P\left(x\right)$P(x) must be divided by $Q\left(x\right)$Q(x) first.
- Note that the term linear factors in row $1$1 includes expressions like $\left(x-4\right)$(x−4), $x$x, $\left(x+1\right)$(x+1) etc, and if these are repeated, as in $\left(x-4\right)^2$(x−4)2 or $\left(x+1\right)^2$(x+1)2 etc, then the decomposition needs to contain two components as shown in row $2$2 the table.
- If the factor is an irreducible quadratic factor (that is, a quadratic factor that cannot be factorised over the reals into a product of linear factors) such as $x^2+4$x2+4, then the numerator of the partial fraction is in the form $Ax+B$Ax+B.
Further examples using the table
Example 2
Decompose $\frac{3x^2-x-5}{\left(x-2\right)\left(x^2+1\right)}$3x2−x−5(x−2)(x2+1) into its partial fractions.
We first note that the degree of $3x^2-x-5$3x2−x−5 is less than the degree of $\left(x-2\right)\left(x^2+1\right)$(x−2)(x2+1) and so we can proceed with the decomposition immediately.
From the table we have that:
| $\frac{3x^2-x-5}{\left(x-2\right)\left(x^2+1\right)}$3x2−x−5(x−2)(x2+1) | $=$= | $\frac{A}{x-2}+\frac{Bx+C}{x^2+1}$Ax−2+Bx+Cx2+1 |
After adding the fractions on the right hand side, and equating numerators, we have:
| $3x^2-x-5$3x2−x−5 | $=$= | $A\left(x^2+1\right)+\left(Bx+C\right)\left(x-2\right)$A(x2+1)+(Bx+C)(x−2) |
| $3x^2-x-5$3x2−x−5 | $=$= | $\left(A+B\right)x^2+\left(C-2B\right)x+\left(A-2C\right)$(A+B)x2+(C−2B)x+(A−2C) |
As before, by equating coefficients, we see that:
| $A+B$A+B | $=$= | $3$3 $(1)$(1) |
| $C-2B$C−2B | $=$= | $-1$−1 $(2)$(2) |
| $A-2C$A−2C | $=$= | $-5$−5 $(3)$(3) |
We need to solve these equations simultaneously. Here is one way to proceed.
Subtracting $(3)$(3) from $(1)$(1) shows $2C=8-B$2C=8−B.
Doubling $(2)$(2) shows $2C=4B-2$2C=4B−2 and therefore $8-B=4B-2$8−B=4B−2.
This means that $5B=10$5B=10 and $B=2$B=2.
From $(1)$(1), therefore, $A=1$A=1 and, using $(3)$(3), this means that $C=3$C=3.
Thus $\frac{3x^2-x-5}{\left(x-2\right)\left(x^2+1\right)}=\frac{1}{x-2}+\frac{2x+3}{x^2+1}$3x2−x−5(x−2)(x2+1)=1x−2+2x+3x2+1.
Example 3 (using substitution to evaluate the constants)
The following example shows how you can sometimes simplify the task of finding the constants.
Decompose $\frac{11x-x^2-15}{\left(x+1\right)\left(x-2\right)^2}$11x−x2−15(x+1)(x−2)2 into its partial fractions.
According to the table above, we commence as:
| $\frac{11x-x^2-15}{\left(x+1\right)\left(x-2\right)^2}$11x−x2−15(x+1)(x−2)2 | $=$= | $\frac{A}{x+1}+\frac{B}{x-2}+\frac{C}{\left(x-2\right)^2}$Ax+1+Bx−2+C(x−2)2 |
| $\frac{11x-x^2-15}{\left(x+1\right)\left(x-2\right)^2}$11x−x2−15(x+1)(x−2)2 | $=$= | $\frac{A\left(x-2\right)^2+B\left(x+1\right)\left(x-2\right)+C\left(x+1\right)}{\left(x+1\right)\left(x-2\right)^2}$A(x−2)2+B(x+1)(x−2)+C(x+1)(x+1)(x−2)2 |
Equating numerators we have:
| $11x-x^2-15$11x−x2−15 | $=$= | $A\left(x-2\right)^2+B\left(x+1\right)\left(x-2\right)+C\left(x+1\right)$A(x−2)2+B(x+1)(x−2)+C(x+1) |
Now rather than equating coefficients, we substitute a few well-chosen values into this last expression. Note that the numerator expressions are true for all values of $x$x.
If $x=-1$x=−1, then by direct substitution $-27=9A$−27=9A, from which $A$A becomes $-3$−3.
Again, if $x=2$x=2, then the last equation becomes $3=3C$3=3C, and so $C=1$C=1.
The only constant left to find is $B$B, so we simply substitute once again, choosing any other value of $x$x, say $x=3$x=3, so that the equation becomes $9=A+4B+4C$9=A+4B+4C. This means that $9=-3+4B+4$9=−3+4B+4, and hence $B=2$B=2.
Therefore $\frac{11x-x^2-15}{\left(x+1\right)\left(x-2\right)^2}=\frac{-3}{x+1}+\frac{2}{x-2}+\frac{1}{\left(x-2\right)^2}$11x−x2−15(x+1)(x−2)2=−3x+1+2x−2+1(x−2)2.
Example 4
Decompose $\frac{3x^2-1}{x\left(x-1\right)^3}$3x2−1x(x−1)3 into its partial fractions.
Even though $\left(x-1\right)^3$(x−1)3 is not specifically listed in the table, we begin by looking for constants $A$A, $B$B, $C$C and $D$D such that:
$\frac{3x^2-1}{x\left(x-1\right)^3}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{\left(x-1\right)^2}+\frac{D}{\left(x-1\right)^3}$3x2−1x(x−1)3=Ax+Bx−1+C(x−1)2+D(x−1)3
By adding the fractions and equating the numerators we see that:
| $3x^2-1$3x2−1 | $=$= | $A\left(x-1\right)^3+Bx\left(x-1\right)^2+Cx\left(x-1\right)+Dx$A(x−1)3+Bx(x−1)2+Cx(x−1)+Dx |
A good substitution is $x=0$x=0 from which we learn that $A=1$A=1. Also substituting $x=1$x=1 shows $D=2$D=2.
At this point, to find $B$B and $C$C, we could either expand the right hand side and equate coefficients, or make two more substitutions to develop two simultaneous equations and find $B$B and $C$C that way. The choice is really made on the basis of how much work is involved.
Here, we suggest two more substitutions.
For $x=-1$x=−1 and $x=2$x=2 we have the following two equations:
| For $x=-1$x=−1 $2$2 | $=$= | $-8A-4B+2C-D$−8A−4B+2C−D |
| for $x=2$x=2 $11$11 | $=$= | $A+2B+2C+2D$A+2B+2C+2D |
and substituting $A=1$A=1 and $D=2$D=2 we form the two simultaneous equations given by:
| $4B-2C$4B−2C | $=$= | $-12$−12 $(1)$(1) |
| $2B+2C$2B+2C | $=$= | $6$6 $(2)$(2) |
Adding $(1)$(1) and $(2)$(2) shows $6B=-6$6B=−6 and so $B=-1$B=−1. Substituting this into $(2)$(2) reveals $C=4$C=4.
Hence we have established that:
$\frac{3x^2-1}{x\left(x-1\right)^3}=\frac{1}{x}-\frac{1}{x-1}+\frac{4}{\left(x-1\right)^2}+\frac{2}{\left(x-1\right)^3}$3x2−1x(x−1)3=1x−1x−1+4(x−1)2+2(x−1)3
.
More examples
Question 1
We want to find the partial fraction decomposition for $\frac{7x-9}{x\left(x+3\right)}$7x−9x(x+3).
Let $\frac{7x-9}{x\left(x+3\right)}=\frac{A}{x}+\frac{B}{x+3}$7x−9x(x+3)=Ax+Bx+3.
First find the value of $A$A.
Now find the value of $B$B.
Hence write down the partial fraction decomposition.
Question 2
We want to find the partial fraction decomposition for $\frac{4x+5}{\left(x+6\right)\left(2x-1\right)}$4x+5(x+6)(2x−1).
Let $\frac{4x+5}{\left(x+6\right)\left(2x-1\right)}=\frac{A}{x+6}+\frac{B}{2x-1}$4x+5(x+6)(2x−1)=Ax+6+B2x−1.
First find the value of $A$A.
Now find the value of $B$B.
Hence write down the partial fraction decomposition, simplifying your answer. Leave the denominators in factorised form.
Question 3
We want to find the partial fraction decomposition for $\frac{2x}{\left(x-6\right)\left(x-4\right)^2}$2x(x−6)(x−4)2.
Let $\frac{2x}{\left(x-6\right)\left(x-4\right)^2}=\frac{A}{x-6}+\frac{B}{x-4}+\frac{C}{\left(x-4\right)^2}$2x(x−6)(x−4)2=Ax−6+Bx−4+C(x−4)2.
First find the value of $A$A.
Next find the value of $C$C.
Now find the value of $B$B.
Hence write down the partial fraction decomposition. Leave the denominators in factorised form.