
Surface Area of Rectangular Prisms
Recall that a rectangular prism is a solid with rectangles for all of its faces.
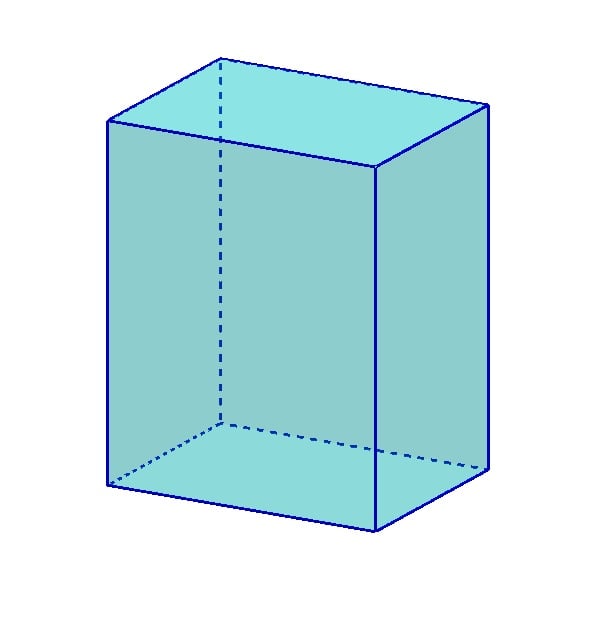
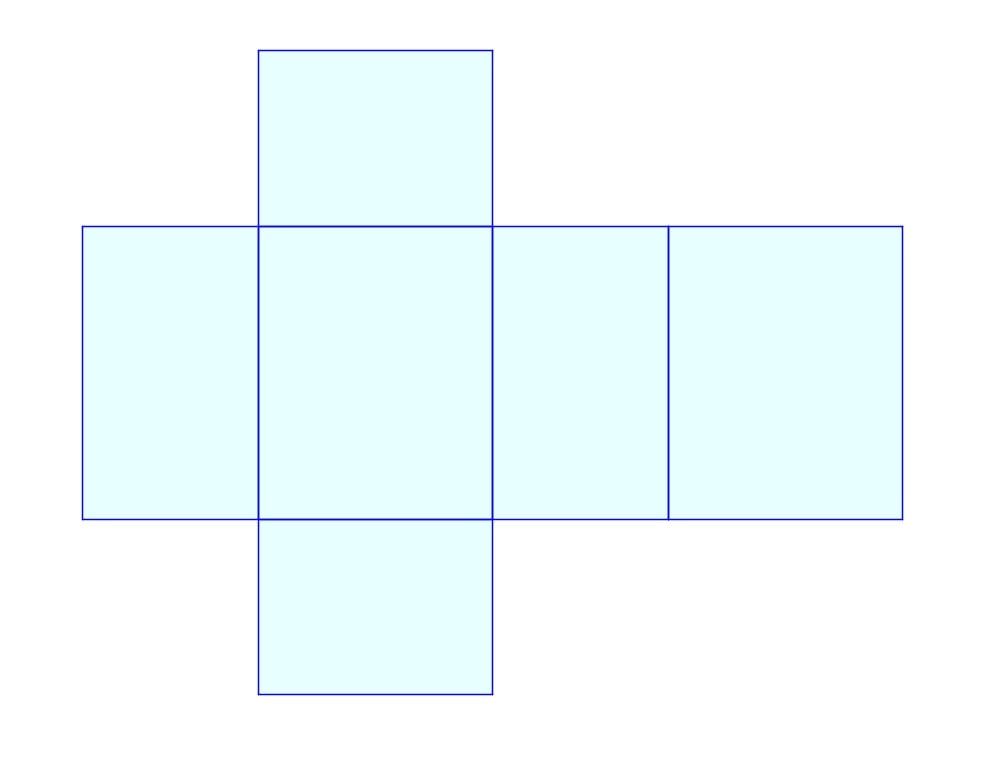
Try the GeoGebra applet below to see the nets of various rectangular prisms.
We learnt recently that the surface area of any prism is just the sum of the areas of all the faces. Hence, to find the surface area of a rectangular prism, we are going to have to have to add up the areas of all the rectangular faces.
Fortunately, this won't take as long as it sounds.
First, let's look at the easiest type of rectangular prism, a cube.


A cube has congruent squares for all of its faces. To find its surface area, we just need to add up the areas of these squares.
Since all six squares have equal areas, the surface area will just be six times the area of one face. Remember that the area of one face is just the square of the side length.
$\text{Surface Area of a Cube}$Surface Area of a Cube$=$=$6\times\text{Area of one Face}$6×Area of one Face$=$=$6\times\left(\text{Side Length}\right)^2$6×(Side Length)2


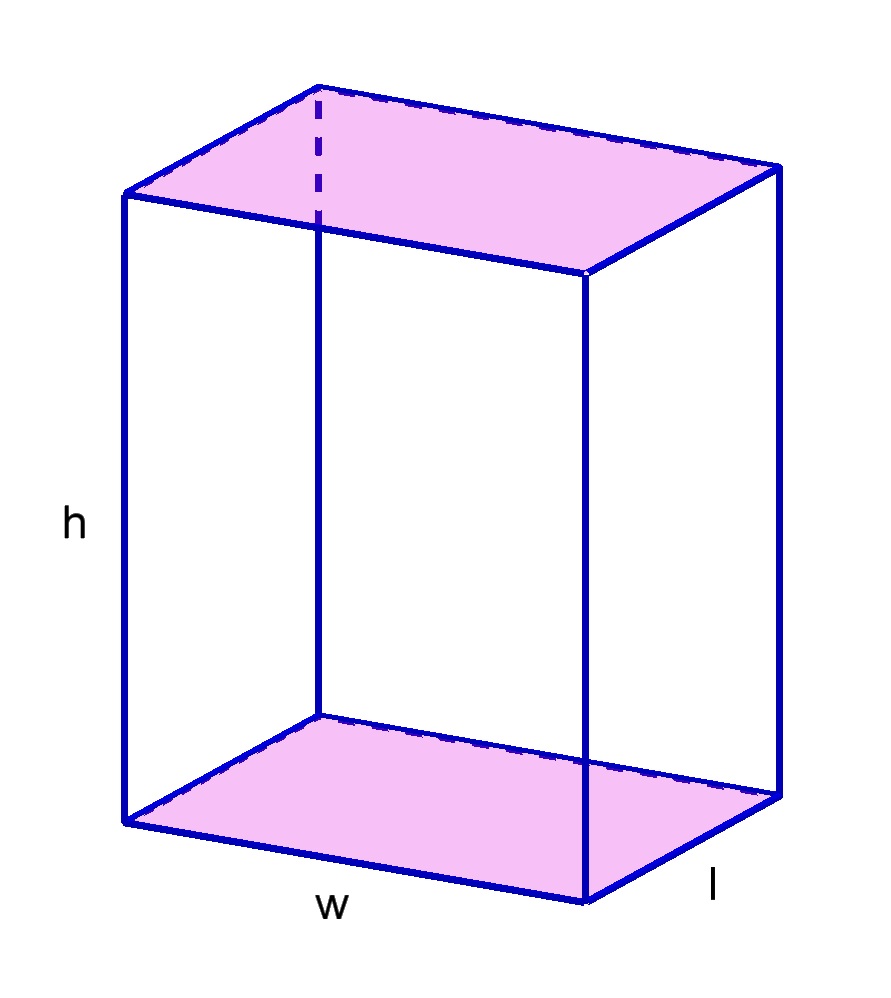
Finding the surface area of rectangular prisms in general can also be made easier by the fact that opposite faces are congruent.
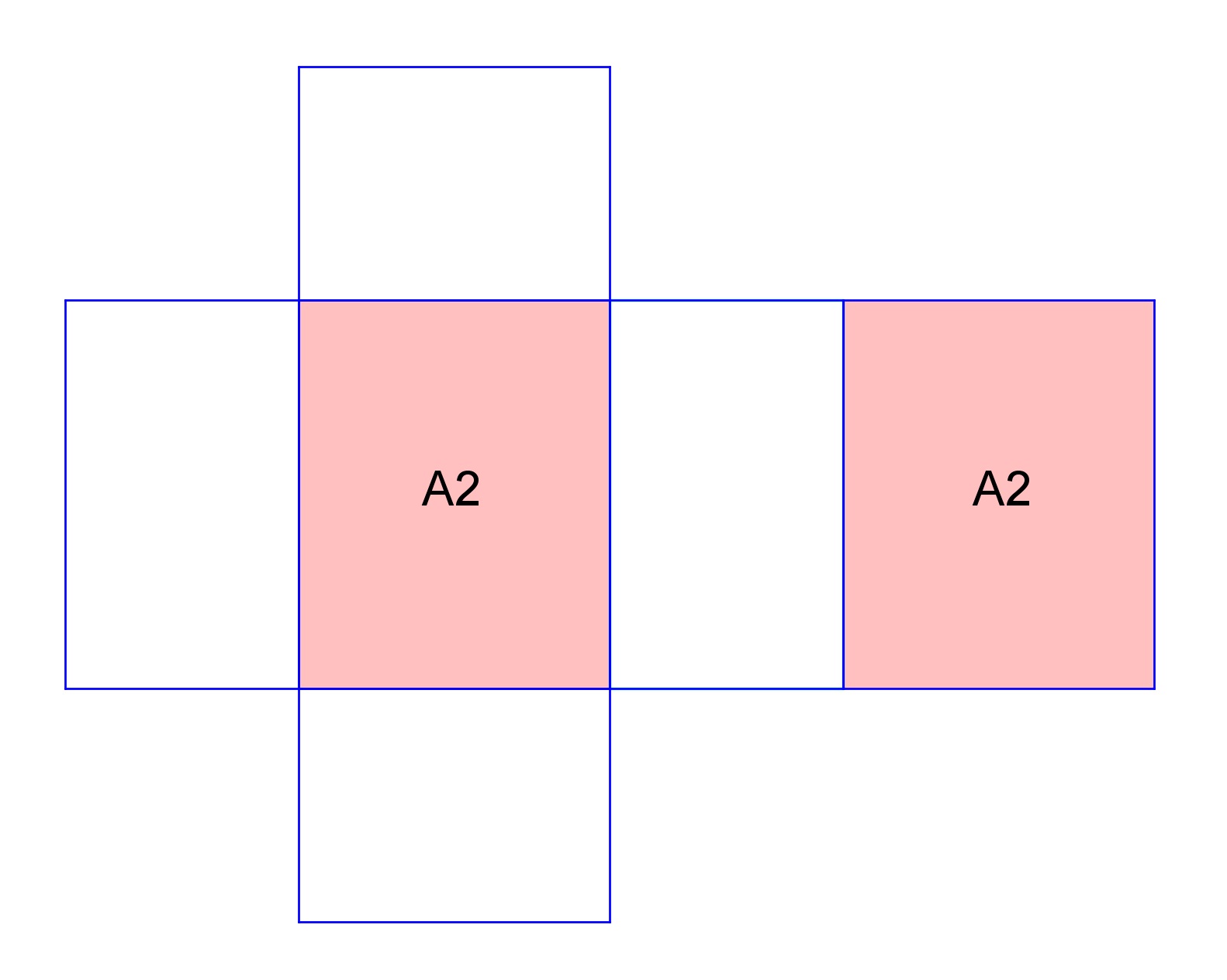
This means we just have to add the areas of the faces in pairs, one for the faces outlined by the length and the width, one by the width and the height, and one by the length and the height.
$\text{Surface Area of a Rectangular Prism}$Surface Area of a Rectangular Prism$=$=$2\times A_1+2\times A_2+2\times A_3$2×A1+2×A2+2×A3$=$=$2lw+2wh+2lh$2lw+2wh+2lh
 |
 |
 |
 |
 |
 |
Examples
Question 1
Consider the following cube with a side length equal to $6$6 cm. Find the total surface area.

Question 2
Consider the following rectangular prism with length, width, and height, equal to $12$12 m, $6$6 m, and $4$4 m, respectively.
Find the surface area of the prism.

Question 3
Laura is building a storage chest in the shape of a rectangular prism. The chest will be $55$55 cm long, $41$41 cm deep, and $39$39 cm high.
What will the surface area of the chest be?