The Right-Angled Triangle
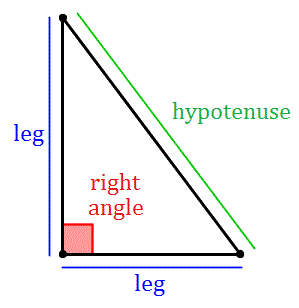
What is the hypotenuse?
The hypotenuse is a technical word to mean
- the longest side of the right-angled triangle
- the side opposite the right angle
It is important for a lot of the work we are about to do in trigonometry that you can identify the hypotenuse of any right-angled triangle. Like we have in these ones here.

Pythagoras' Theorem
A long time ago, a Greek mathematician named Pythagoras came up with an interesting observation about right-angled triangles: if $c$c represents the length of the hypotenuse, and $a$a and $b$b represent the other two sides (that meet at a right angle), then $a^2+b^2=c^2$a2+b2=c2.
In other words, the square of the hypotenuse ($c$c) of a right-angled triangle is equal to the square of side $a$a plus the square of side $b$b.
The following interactive demonstrates using areas Pythagoras' Theorem. You can use the slider and move the squares of a and b to cover the area of c squared, thus demonstrating that $a^2+b^2=c^2$a2+b2=c2
(Watch this video to see the interactive in action - )

To see how such a simple formula can be used to solve real world problems, suppose a carpenter wants to build a ramp to replace the set of stairs to his front porch. If the porch is $1$1 metre off the ground and the ramp is to start $4$4 metres from the base of the porch (in order to connect the ramp to the driveway), what is the length of the ramp he has to build?
To find out, we substitute the numbers into the formula: $c^2=1^2+4^2$c2=12+42, so $c^2=17$c2=17. Taking the square root of both sides, $c=\sqrt{17}$c=√17 so the ramp should be about $4.12$4.12 metres long.
$a^2+b^2=c^2$a2+b2=c2
for all right-angled triangles, where $c$c is the hypotenuse of the triangle.
So to test if a triangle is right-angled, we can use the Pythagorean Formula and the lengths of the sides. If the formula holds true, it is a right-angled triangle.
Example
Question 1
Which side of the triangle in the diagram is the hypotenuse?

$AB$AB
A$CA$CA
B$BC$BC
C
Question 2
Use Pythagoras' theorem to determine whether this is a right-angled triangle.

Let $a$a and $b$b represent the two shorter side lengths. First find the value of $a^2+b^2$a2+b2.
Let $c$c represent the length of the longest side. Find the value of $c^2$c2.
Is the triangle a right-angled triangle?
Yes
ANo
B
Question 3
Is a triangle with side lengths of $3$3 cm, $4$4 cm and $5$5 cm a right-angled triangle?
Think: I will need to identify the longest side, this value will be c in the Pythagorean formula.
Do:
| $LHS$LHS | $=$= | $a^2$a2 + $b^2$b2 |
| $=$= | $3^2$32 + $4^2$42 | |
| $=$= | $9+16$9+16 | |
| $=$= | $25$25 |
| $RHS$RHS | $=$= | $5^2$52 |
| $=$= | $25$25 | |
| Therefore | ||
| $LHS$LHS | $=$= | $RHS$RHS |
Therefore this is a right-angled triangle.