Polygons II

The word polygon comes from the Greek poly - meaning many and gonos - meaning angles.  So a polygon is a many angled figure.  

With many angles comes many sides, in fact every 2D straight sided shape has the same number of angles as sides.  

These are the names of many common n-gons.

Polygons can be classified as being either regular or irregular.

Regular

A regular polygon has all sides (and angles) equal length and size. 

These are all regular polygons.

Irregular

An irregular polygon has some sides (and angles) of different lengths and sizes.

These are all irregular polygons.

Polygons can be classified as either concave or convex.  

Convex

                                                           

 

Concave

 

Definition

A convex shape can be identified through two possible key elements

• that when drawing a line between two neighboring vertices that the entire line drawn is always OUTSIDE the shape.  
• that there is no angle greater than 180 degrees, (no reflex angles)

If the shape has a caved in side we call it concave.  Formally we define a concave shape as when the line that connects 2 neighboring vertices projects into the inside of the shape.  Another way to tell if a shape is convex or concave is to look at the value of the interior angles.  If all interior angles are less than 180° then the shape is convex.  If the shape has at least 1 angle greater than 180° then it is concave.  

Have a play with the interactive below, create convex polygons and concave polygons by moving the blue points. Note the line extensions and angles as discussed above. Watch video

Sum of interior angles of a polygon

We already know that the sum of angles in a triangle is $180$180°.

What about the sum of angles in a quadrilateral? Well a quadrilateral can be thought of as two triangles, so the internal angle sum is $180+180=360$180+180=360°

This interactive will show you different interior angle sums for different polygons.  You can also see how many triangles fit into it. 

Watch this video if you would like to see this interactive in action - Watch video

If $n$n represents the number of sides, then the number of triangles in any polygon is $n-2$n−2.

If each triangle has $180$180°, then the total interior angle sum of a polygon is $180\times\left(n-2\right)$180×(n−2)

Worked Examples

Question 1

Question 2

Consider the adjacent figure.

1. Solve for $x$x.

2. Solve for $y$y.

Reveal SolutionWatch video

Question 3

Consider the following non-convex figure.

1. Which expression represents the exterior angle sum of the given figure?

   $\left(180-x\right)+126+28+89=360$(180−x)+126+28+89=360

   A

   $x+\left(180-54\right)+152+91=360$x+(180−54)+152+91=360

   B

   $x-54+152+91=360$x−54+152+91=360

   C

   $x+54+152+91=360$x+54+152+91=360

   D

2. Using the expression found in part (a), solve for $x$x.

Reveal SolutionWatch video

Solving problems

When solving angle problems in geometry one of the most important components is the reasoning (or rules) you use to solve the problem.  You will mostly be required in geometry problems to not only complete the mathematics associated with calculating angle or side lengths but also to state the reasons you have used.  Read through each of these rules and see if you can describe why and draw a picture to represent it.  

Angles in parallel lines

Cointerior angles in parallel lines are supplementary (U, C)
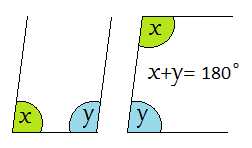Corresponding angles on parallel lines are equal (F)
Alternate angles on parallel lines are equal (Z)
Vertically opposite angles are equal (X)

Geometry Rules with Angles

Exterior angle of a triangle is equal to the sum of the two opposite interior angles
Angle sum of an n-sided polygon is (n-2)[x]180
Sum of exterior angles of a polygon is 360°
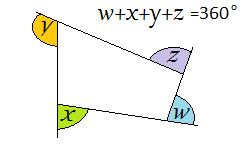Angle sum of a quadrilateral is 360°
Angles at a point sum to 360°
Vertically opposite angles are equal
Adjacent angles forming a right angle are complementary
Adjacent angles on a straight line are supplementary

Properties of Triangles

Angle sum of a triangle is 180°
Base angles are equal in an isosceles triangle   Sides opposite base angles are equal in an isosceles triangle
All angles in an equilateral triangles are equal   All angles in an equilateral triangle are equal to 60°   All sides in an equilateral triangle are equal

Properties of quadrilaterals

All Quadrilaterals

Angle sum of an n-sided polygon is (n-2)[x]180
Sum of exterior angles of a polygon is 360°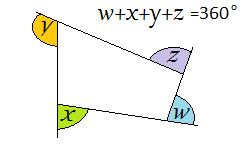
Angle sum of a quadrilateral is 360°

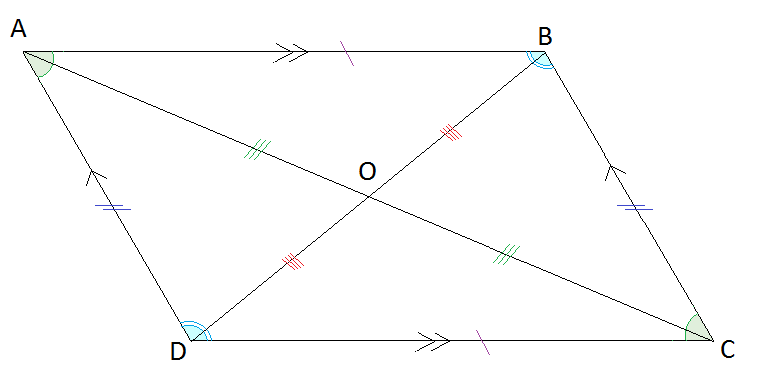
Parallelogram

• Opposite sides in a parallelogram are parallel
• Opposite angles in a parallelogram are equal
• Opposite sides in a parallelogram are equal
• Diagonals of a parallelogram bisect each other 

Rectangle

• Opposite sides in a rectangle are parallel
• Opposite sides in a rectangle are equal
• Diagonals of a rectangle bisect each other 
• Diagonals in a rectangle are equal 

Square

• All sides of a square are equal
• Opposite sides in a square are parallel
• Diagonals of a square are perpendicular to each other (cross at 90°)
• Diagonals of a square bisect the angles at the vertices (makes them 45°)
• Diagonals of a square bisect each other 
• Diagonals of a square are equal 

Rhombus

• Opposite angles of a rhombus are equal
• Opposite sides in a rhombus are parallel
• All sides of a rhombus are equal
• Diagonals of a rhombus bisect each other at 90 degrees 
• Diagonals of a rhombus bisect corner angles 
• Diagonals of a rhombus bisect each other

Trapezium

• An isosceles trapezium (trapezoid) has 2 pairs of adjacent angles equal
• A trapezium (trapezoid) has one pair of opposite sides parallel
• An isosceles trapezium (trapezoid) has one pair of opposites sides equal
• Diagonals of an isosceles trapezium (trapezoid) are equal

Kite

• A kite has 2 pairs of adjacent sides equal
• A kite has 1 pair of opposite angles equal
• The longest diagonal of a kite bisects the angles through which it passes 
• Diagonals of a kite are perpendicular to each other 
• The longest diagonal of a kite bisects the shorter diagonal

Worked Examples

QUESTION 1

QUESTION 2

Consider the adjacent figure.

1. Solve for $x$x.

2. Solve for $y$y.

Reveal SolutionWatch video

QUESTION 3

Consider the following non-convex figure.

1. Which expression represents the exterior angle sum of the given figure?

   $\left(180-x\right)+126+28+89=360$(180−x)+126+28+89=360

   A

   $x+\left(180-54\right)+152+91=360$x+(180−54)+152+91=360

   B

   $x-54+152+91=360$x−54+152+91=360

   C

   $x+54+152+91=360$x+54+152+91=360

   D

2. Using the expression found in part (a), solve for $x$x.

Reveal SolutionWatch video