Topics
Location and Movement
topic badge
CanadaON
Grade 3

Translation

Lesson
Practice
Lesson

Translations

A translation is what happens to a shape or object, when we slide it from one place to another. It's as if we are pushing, or moving, our shape around. We aren't flipping, rotating, enlarging or reducing our shape at all.

A good way to remember this is to think of each part of our shape moving by the same amount, in the same direction. If you look at the sofa below, it has moved to the right. This is a translation, since each part of the sofa has moved in the same direction, by the same distance.

Let's look at some shapes and see whether or not they are translations. We will also look at how to describe how an object has been moved, or been translated.

 

Using a grid

A grid can help us describe a translation because we can look at how many units, or spaces an object has moved. We can also look at the direction it has moved. For example, the flower pot below has moved down $2$2 units. Sometimes an object might move more than once. Let's look at this in more detail now.

 

 

 

 

 

Remember!

A translation means the whole shapes moves by the same amount, in the same direction. The shape can't change size, rotate, or include a reflection at all.

 

Worked Examples

QUESTION 1

Which picture shows a translation?

  1. A

    B

    C

    D

QUESTION 2

 

Which of the following represents a translation of the flag 1 unit up and 2 units to the right?

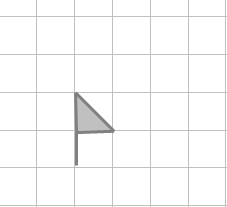
A flag is situated on a square grid. The whole flag takes up two squares on the grid. The flag itself, which is the shaded triangular shape, is located at the third column from the left and the third row from the bottom. The pole of the flag is located just right below the triangle itself. That is, the pole of the flag is at the third column from the left and second row from the bottom.

  1. A flag is situated on a square grid. The whole flag takes up two squares on the grid. The flag itself, which is the shaded triangular shape, is located at the third column from the left and the third row from the bottom. The pole of the flag is located just at the right side of the triangle itself. That is, the pole of the flag is at the fourth column from the left and third row from the bottom.
    A

    A flag is situated on a square grid. The whole flag takes up two squares on the grid. The flag itself, which is the shaded triangular shape, is located at the fifth column from the left and the fourth row from the bottom. The pole of the flag is located just right below the triangle itself. That is, the pole of the flag is at the fourth column from the left and third row from the bottom.
    B

    A flag is situated on a square grid. The whole flag takes up two squares on the grid. The flag itself, which is the shaded triangular shape, is located at the third column from the right and the second row from the bottom. The pole of the flag is located just right above the triangle itself. That is, the pole of the flag is at the third column from the right and third row from the bottom.
    C

Question 3

What translation is involved in moving the square from:

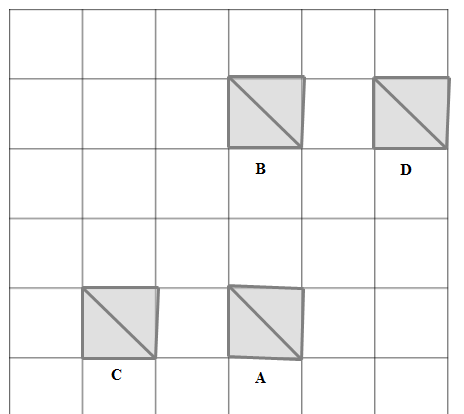
A 6x6 grid containing four shaded squares, each marked by a diagonal line extending from the upper left corner to the lower right corner. These squares are designated with the letters $A$A, $B$B, $C$C, and $D$D. Square $A$A is located at the intersection of the 4th column and the 5th row. Square $B$B is found at the 4th column and the 2nd row. Square $C$C is placed at the 2nd column and the 5th row. Lastly, Square $D$D is situated at the 6th column and the 2nd row.

  1. position $A$A to position $B$B?

    $1$1 unit to the right

    A

    $3$3 units up

    B

    $3$3 units down

    C

    $2$2 units to the left

    D

  2. position $A$A to position $C$C?

    $2$2 units up

    A

    $2$2 units to the right

    B

    $2$2 units to the left

    C

    $2$2 units down

    D

  3. position $A$A to position $D$D?

    $2$2 units up and $1$1 unit to the left

    A

    $3$3 units up and $3$3 units to the right

    B

    $2$2 units down and $3$3 units to the right

    C

    $3$3 units up and $2$2 units to the right

    D

Outcomes

3.GS3.01

Describe movement from one location to another using a grid map

3.GS3.02

Identify flips, slides, and turns, through investigation using concrete materials and physical motion, and name flips, slides, and turns as reflections, translations, and rotations

What is Mathspace

About Mathspace