The Road to Safety...
So far, we’ve been looking at the financial side of purchasing and operating a car. Now let’s look at what’s involved in getting behind the wheel of a car.
Whenever we talk about a car’s motion we usually want to know details on:
- How far has the car travelled?
- How long did it take?
- How fast was it travelling?
These represent three important properties:
SPEED, DISTANCE and TIME
Taking a closer look, the three properties form tight-knit relations
We know, by its definition, that speed is measured by looking at how far something travelled compared to how long it took (2.3 metres/second, 60 kilometres/hour, 100 miles per hour etc.).
By knowing one of these three variables we can find the others.
For example:
- A car travels 30 km in 1 hour, therefore it is travelling at 30 km/h.
- A car travels for 3 hours at 100 km/h, therefore it travelled 300 kilometres
These are everyday relations that can help us figure out a number of things.
The Distance Travelled = Speed x Time or $D=S\times T$D=S×T
By rearranging this formula, we can find speed $S=\frac{D}{T}$S=DT
And also find time $T=\frac{D}{S}$T=DS
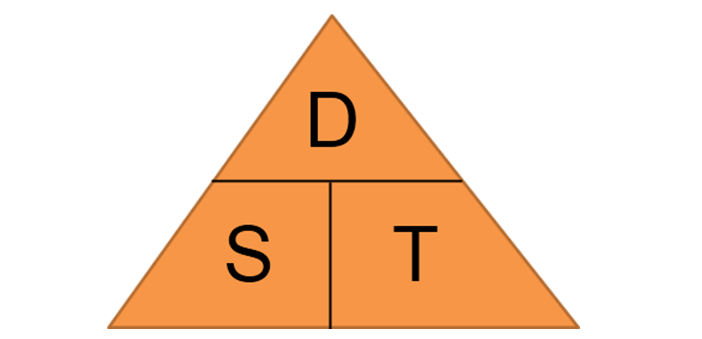An easy way to remember these relations is by this triangle. Cover up the variable you want to find and the remaining variables will give the operation required (to find speed, cover the ‘S’ and what remains is D divided by T).
These variables can be graphed to show trends and determine characteristics of a person’s trip.
On this distance vs. time graph, the line has a constant ‘slope’. Since slope is rise over run, in this case it will be Distance/Time, which equals speed. So the slope of a distance-time graph gives the corresponding speed.
On this speed vs. time graph, the area under the graph is equivalent to the total distance travelled.
Knowing these relations is important, but equally important is being able to collect the information and convert it into units that we can use.
In a lot of cases, we will need to speak in terms of metres and seconds (particularly when we start looking at braking distances and acceleration).