
Total stopping distance
A lot of drivers aren’t fully aware of the distance they cover when braking.
Consider a driver travelling at 60 km/h. The driver sees the traffic lights ahead turn amber and begins to brake. To come to a complete halt, the driver needs a minimum of around 40 metres when travelling at that speed.
But how do we know this?
We can calculate stopping distance in a similar way to finding any distance, speed or time.
Factors that affect stopping distance:
- Speed (how fast the car is travelling initially)
- Road conditions (wet surfaces will have different characteristics to dry surfaces, as will loose gravel etc.)
- Driver reaction time/distance (the average human has a reaction time of between 1.1 and 1.4 seconds- this will impact the distance the car travels before the brakes are applied)
We know that:
Total stopping distance = Reaction time distance + Braking distance
Reaction Time Distance
On average, under driving conditions, it takes a human 1.2 seconds to observe an obstacle and react. So if we take reaction time to be 1.2 seconds, after knowing how fast the car is travelling we can calculate the reaction time distance.
For example: A reaction time of 1.2 seconds travelling at 60 km/h would equate to a stopping distance as follows.
60 \text{km/h } = \frac{60 \times 1000}{60 \times 60} \text{m/s } = 16.7 \text{m/s }
(Note that we are dividing by 60 x 60. This is because the original rate is kilometres divided by hours).
Then, \text{Distance } = \text{Speed } \times \text{Time } = 16.7 \text{m/s } x 1.2 \text{s } = 20 \text{metres }.
Braking Distance
Braking distance is calculated slightly differently…
At the instant the driver begins to brake and the car starts to slow down, we can no longer assume that the speed will be constant. As a result, we have to take into consideration a varying speed- speed that is slowing down...or DECELERATION.
Deceleration (which is essentially the opposite of acceleration, i.e. change in the speed of an object) is usually measured in units of metres per second per second or m/s/s or m/s2.
We can think of this as a rate of change of speed, just like speed is a rate of change of distance.
Speed is metres/second so acceleration (or deceleration) is (metres/second)/second.
In most cases, instead of writing m/s/s we just write m/s2.
So, knowing the deceleration we can use some physics relationships (known as the SUVAT equations) to help understand how long it takes to come to a complete stop, how far we travel whilst braking, or even calculate how fast we should be travelling initially in order to be able to stop in a certain distance or time.
To begin with, acceleration is defined as the change in velocity over time, or:

Acceleration formula
where v is the final velocity, u is the initial velocity and t is the time taken (note that in our case, since we are braking, the initial velocity will be higher than the final velocity, giving acceleration as negative or as a deceleration).
We can rearrange this in a number of ways, for example;

Velocity formula
We can use this equation to find how long it takes to come to a complete stop if we know what the deceleration is.
Example
How long does it take for a car travelling at 60 \text{km/h } to decelerate at 6\text{m }\text{/ }\text{s }2 and come to a complete stop?
-
Convert 60 \text{km/h } to \text{m/s }
\frac{60 \times 1000}{60 \times 60} ≈ 16.7 \text{m/s }
- Rearranging v = u + at in order to find the time taken;
\text{t }= \frac{v - u}{a}
Taking v (final velocity) as zero, since the car will come to a complete stop, then
t = \frac{0 - 16.7}{- 6} [Negative 6 \text{m }\text{/ }\text{s }2 since it is a deceleration] = 2.78 \text{seconds }
Now that we know the time it takes, we substitute the time found into another equation to find the displacement (or the distance travelled from when braking began to where the car finally stops):

Displacement (s) formula
Here, s is known as displacement (the braking distance), and u, a and t are as above.
So to find the actual braking distance, let’s substitute the time we found.
| s | = | 16.7 \times 2.78 + \frac{1}{2} \times \left( - 6 \right) \times 2.78^{2} |
| = | 46.426 + \left( - 23.1852 \right) | |
| = | 46.426 - 23.1852 | |
| = | 23.2408 \text{m } | |
| = | 23.2 \text{m } |
Putting it all together
So we now understand that the total stopping distance is a combination of reaction distance and braking distance.
Reaction distance is simply the reaction time multiplied by the initial speed (remember that they must be in consistent units).
Braking distance involves finding the braking time given the initial (u) and final (v) velocities and the deceleration, then finding the braking distance through the displacement formula.
The following graph shows the average stopping distance for a variety of speeds. The graph assumes a deceleration of 5 m/s2.
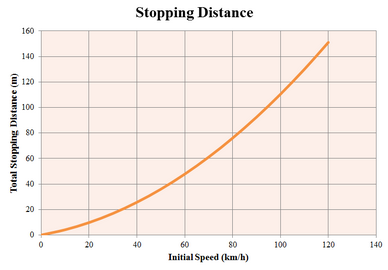
Stopping Distances with a deceleration of 5 m/s2