When we describe the shape of data sets, we focus on how the scores are distributed and whether the shape is symmetrical or not.
Symmetry
Data may be described as symmetrical or asymmetrical.
There are many cases where the data tends to be around a central value with no bias left or right. In other words, $50%$50% of scores will be above the mean and $50%$50% of scores will be below the mean.
The normal distribution is the most common example of symmetrical data. The normal distribution looks like this:
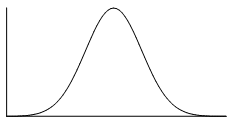
The picture below shows how the normal distribution occurs on a histogram. The dark line shows the nice, symmetrical pattern in the histogram.
The '0' point right in the middle of the distribution represents the mean, the median and the mode- all these measures of central tendency are equal. If we use that '0' line as our axis of symmetry, do you notice how the left hand side is a perfect reflection of the right hand side? That means it's symmetrical.
If your data is asymmetrical (ie. it isn't symmetrical), it may be described as skewed.
Skew
Positive skew
A positive skew means that the majority of the scores are low and the long tail is on the positive side of the peak of the graph. This means the mean is greater than the median, which is greater than the mode.
MODE < MEDIAN < MEAN
A positively skewed graph looks something like this.
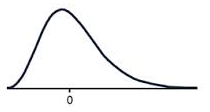
Notice how most of the scores are in the lower half of the graph?
The tail to the right, pulls the mean up, this is the positive skew.
Negative Skew
A negative skew means that the majority of the scores are high and the long tail is on the negative side of the peak. This means the mode is greater than the median, which is greater than the mean.
MEAN < MEDIAN < MODE
A negatively skewed graph looks something like this.
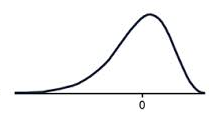
Notice how most of the scores are in the higher half of the graph?
The tail to the left, pulls the mean down, this is the negative skew.
Clustering
A cluster is a number of similar things collected together. Similarly, in data displays, if lots of the scores in a data set are grouped together within a very small range, we also call this clustering.
Outliers
The shape of a data also shows us whether there are any outliers or unusually high or low scores in our data set.
For example, in the dot plot below, do you see how all the scores range between $12$12 and $14$14 except one? This means that $24$24 is an outlier.

In this case the data is very obviously way outside the range of the rest of the data set.
More formally we define that a score is an outlier if it is $1.5\times$1.5× IQR above the upper quartile, or $1.5\times$1.5× IQR below the lower quartile.
Now let's try and use this knowledge to describe some data sets!
Worked Examples
Question 1
State whether the scores in each histogram are positively skewed, negatively skewed or symmetrical (approximately).
A histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. Most of the scores are relatively high. Positively skewed
ASymmetrical
BNegatively skewed
CA histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. Approximately, as the score goes higher, the frequency goes lower. Positively skewed
ANegatively skewed
BSymmetrical
CA histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. The scores have its peak approximately in the middle. Negatively skewed
ASymmetrical
BPositively skewed
C
QUESTION 2
For the Stem and Leaf plot attached:
| Stem | Leaf | |
| $0$0 | $5$5 | |
| $1$1 | $7$7 $8$8 | |
| $2$2 | $0$0 $8$8 | |
| $3$3 | $0$0 $4$4 $6$6 $7$7 $8$8 $9$9 | |
| $4$4 | $1$1 $3$3 $5$5 $8$8 $8$8 $8$8 | |
| $5$5 | ||
| $6$6 | ||
| $7$7 | ||
| $8$8 | ||
| $9$9 | $3$3 | |
|
||
Are there any outliers?
Yes
ANo
BIdentify the outlier.
Is there any clustering of data?
Yes
ANo
BWhere does the clustering occur?
10s - 20s
A30s - 40s
B20s - 30s
CWhat is the modal class(es)?
10-19
A40-49
B30-39
C20-29
DNot including the outlier, the distribution of the data is:
Positively skewed
ASymmetrical
BNegatively skewed
C
