
Volume of Composite Solids III
We have already seen how to find the volume of composite solids of varying shapes and sizes.
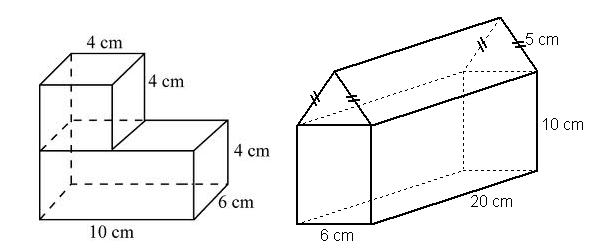
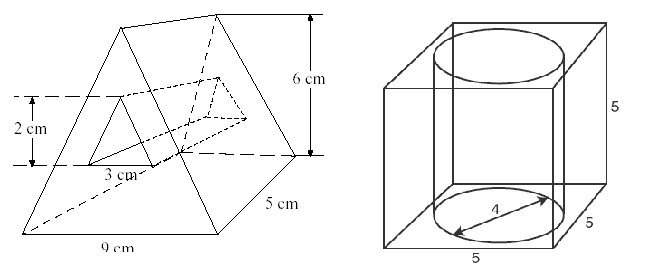
We saw that some are formed by putting together a combination of smaller solids, and that some are formed by removing part of a larger solid.
Now we can look at many different composite solids and consider them in terms of all the solids we know.

$\text{Volume of Prisms }=\text{Area of Base }\times\text{Height of Prism }$Volume of Prisms =Area of Base ×Height of Prism
$\text{Volume of Cube }=s^3$Volume of Cube =s3
$\text{Volume of Rectangular Prism }=lwh$Volume of Rectangular Prism =lwh
$\text{Volume of Cylinder }=\pi r^2h$Volume of Cylinder =πr2h
$\text{Volume of Right Pyramid }=\frac{1}{3}\times\text{Base Area}\times\text{Height of Pyramid}$Volume of Right Pyramid =13×Base Area×Height of Pyramid
$\text{Volume of Right Cone }=\frac{1}{3}\pi r^2h$Volume of Right Cone =13πr2h
$\text{Volume of Sphere }=\frac{4}{3}\pi r^3$Volume of Sphere =43πr3
Worked Examples
Question 1
Find the volume of the figure shown, correct to two decimal places.

Question 2
Find the volume of the composite figure shown, correct to two decimal places.
