When solving angle problems in geometry one of the most important components is the reasoning (or rules) you use to solve the problem. You will mostly be required in geometry problems to not only complete the mathematics associated with calculating angle or side lengths but also to state the reasons you have used. Read through each of these rules and see if you can describe why and draw a picture to represent it.

Properties of quadrilaterals

All Quadrilaterals

Angle sum of an n-sided polygon is $\left(n-2\right)\times180$(`n`−2)×180
Sum of exterior angles of a polygon is $360$360°
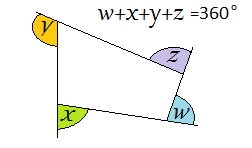Angle sum of a quadrilateral is $360$360°

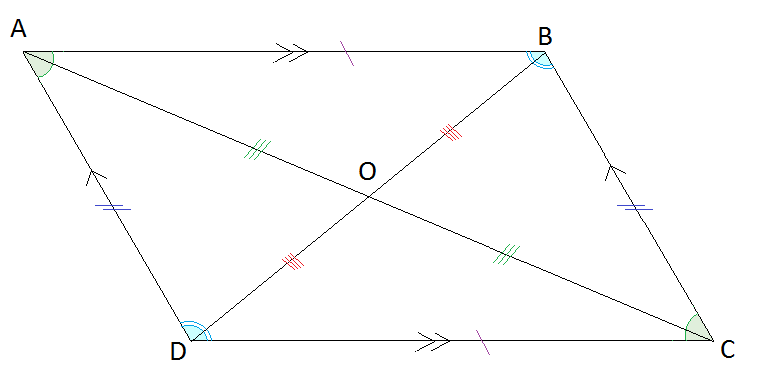
Parallelogram

Opposite sides in a parallelogram are parallel
Opposite angles in a parallelogram are equal
Opposite sides in a parallelogram are equal
Diagonals of a parallelogram bisect each other

Rectangle

Opposite sides in a rectangle are parallel
Opposite sides in a rectangle are equal
Diagonals of a rectangle bisect each other
Diagonals in a rectangle are equal

Square

All sides of a square are equal
Opposite sides in a square are parallel
Diagonals of a square are perpendicular to each other (cross at 90°)
Diagonals of a square bisect the angles at the vertices (makes them 45°)
Diagonals of a square bisect each other
Diagonals of a square are equal

Rhombus

Opposite angles of a rhombus are equal
Opposite sides in a rhombus are parallel
All sides of a rhombus are equal
Diagonals of a rhombus bisect each other at 90 degrees
Diagonals of a rhombus bisect corner angles
Diagonals of a rhombus bisect each other

Trapezium

An isosceles trapezium (trapezoid) has 2 pairs of adjacent angles equal
A trapezium (trapezoid) has one pair of opposite sides parallel
An isosceles trapezium (trapezoid) has one pair of opposites sides equal
Diagonals of an isosceles trapezium (trapezoid) are equal

Kite

A kite has 2 pairs of adjacent sides equal
A kite has 1 pair of opposite angles equal
The longest diagonal of a kite bisects the angles through which it passes
Diagonals of a kite are perpendicular to each other
The longest diagonal of a kite bisects the shorter diagonal

A summary of the geometrical properties of angles can be found here.

A summary of the geometrical properties of triangles can be found here.

A summary of the geometrical properties of angles in parallel lines can be found here.

Worked Examples

Question 1

Consider what you know about parallelograms.

Which of the following quadrilaterals are not parallelograms? Select all that apply.

A four-sided polygon with blue squares at the four corners indicating that they are right angles. There are single line markings at the top and bottom sides indicating that these sides are of equal length. There are double line markings at the left and right sides indicating that these sides are of equal length.

A

A four-sided polygon with blue squares at the four corners indicating that they are right angles. There are single line markings on all four sides indicating that these sides are of equal length.

B

A four-sided polygon with single line markings at the top and bottom sides indicating that these sides are of equal length. There are double line markings at the left and right sides indicating that these sides are of equal length.

C

A four-sided polygon with single line markings on all four sides indicating that these sides are of equal length.

D

A four-sided polygon is depicted. The top side appears shorter than the bottom side. And the left side appears to be more slanted and longer than the right side.

E
In part (a), we found that the quadrilateral pictured below is not a parallelogram. What type of quadrilateral is it?

A four-sided polygon is depicted. The top side appears shorter than the bottom side. And the left side appears to be more slanted and longer than the right side.

A kite
A
A rhombus
B
A rectangle
C
A trapezium
D