Congruent triangles are triangles that are identical in shape and size. In other words, all corresponding (matching) sides and angles are equal.
We can confirm congruent shapes by seeing that if by using a combination of flips, slides or turns, we can reorient one shape to look like the other. If you have to use enlargements to stretch or change the size of the shape than they are not congruent.
If your triangles are not on a number plane, the equal sides may be indicated by a series of small lines. For example, in the triangle below, the two sides with one line are equal, so we can say that $x=6$x=6cm. Similarly, the two sides with two lines are equal.
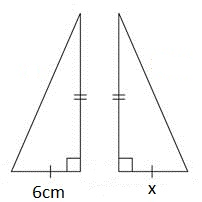
Similarly, equal angles will be indicated by a common symbol or variable.
Once we can identify common sides and common angles in triangles, we can prove that they are congruent. Similarly, once we know that triangles are congruent, we can find any unknown values by finding the corresponding value in the congruent triangle.
Here are the four proofs of congruency. You only need to use one of them to prove two triangles are congruent.
SSS - all sides are equal
AAS - two angles and one side are equal
SAS - two pairs of corresponding sides, and the pair of included angles (angle is between the two sides) are equal
RHS - right-angled triangles with equal hypotenuses and a pair of equal corresponding sides
Let's look at some more examples now to see whether we can determine which triangles are congruent.
Examples
Question 1
a) Which of the following triangles are congruent?
b) State the reason why
Question 2
Consider the figure. Is there enough information to prove that $\triangle WXY$△WXY is congruent to $\triangle EBF$△EBF?
Question 3
a) From the information given on the diagram, which side is equal to $AB$AB?
b) State the reason why $\triangle ABC$△ABC is congruent to $\triangle DFE$△DFE.