Problems with Systems of Inequalities in 2 Variables
Systems of linear inequalities are the key ingredients in certain optimisation problems, known as linear programming problems. Typically, these problems are to do with the allocation of resources subject to constraints. Methods for dealing with them were developed during the second world war and were initially kept secret.
Among others, significant names in the history of this branch of mathematics were the Russian Leonid Kantorovich during the war and, a few years later, the American George B. Dantzig.
Linear programming problems can have many variables but we introduce some of the important ideas by examining cases in which there are just two variables. We may want to know how to describe a set of feasible solutions to a problem or we may wish to go further and investigate which feasible solution is best because it maximises a monetary value or minimises a cost or uses time most efficiently, and so on.
Often, the first step in solving such a problem is to translate information expressed in words into an algebraic form using inequalities. We choose variables to represent the numerical quantities involved and we write inequalities, often called constraints, describing how the variables are related to one another.
Example 1
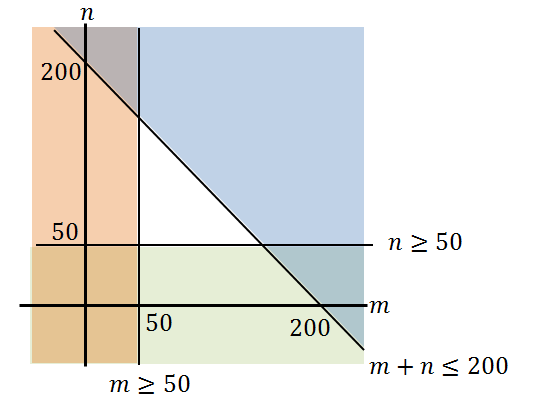
We are told that there are 200 workers in an organisation. Some are to be employed in the production of product $A$A and some are to be employed producing product $B$B. There may be others who are employed on the production of neither $A$A nor $B$B.
We choose variables $m$m and $n$n to represent the numbers of workers associated with products $A$A and $B$B respectively. (Note that we do not use the symbols $A$A and $B$B for this as they represent categories and do not represent numbers.)
Now, the information given translates into the algebraic form $m+n\le200$m+n≤200.
This relation constrains the values that can be taken by the variables $m$m and $n$n. Usually, there will be further constraints due to other requirements of the production process. For example, it may be that in order to produce any quantity at all of either product, at least $50$50 workers must be assigned to each product.
This requirement gives rise to the additional constraints: $m\ge50$m≥50 and $n\ge50$n≥50. All three constraints can be displayed graphically as follows. The region of feasible solutions is left unshaded.
Example 2
In addition to the constraints given in Example 1, we are told that each unit of product $A$A requires $2.4$2.4 person-hours and each unit of product $B$B requires $3$3 person-hours. If each worker can work a $36$36 hour week, there must be at most $200\times36=7200$200×36=7200 person-hours available.
Suppose the number of units produced in a week of product $A$A is $\alpha$α and the number of units of product $B$B is $\beta$β. The time spent producing product $A$A must be $2.4\alpha$2.4α and the time spent producing $B$B must be $3\beta$3β. So, the total of the person-hours spent producing products $A$A and $B$B is the sum of these, which has to be less than or equal to the $7200$7200 hours available. Thus, $2.4\alpha+3\beta\le7200$2.4α+3β≤7200.
This is equivalent to the constraint $m+n\le200$m+n≤200 but it is expressed in terms of the numbers of products produced instead of the numbers of workers engaged in their production.
Worked Examples
Question 1
An airline is checking passengers into two flights, A and B, simultaneously. Due to passenger numbers, there must be at least $10$10 staff at check-in for flight A and at least $7$7 staff at check-in for flight B. Since there must be staff on hand for other services, the airline can only allocate at most $23$23 staff for check-in of both flights.
Let $x$x and $y$y represent the number of staff attending check-in of flights A and B respectively.
Fill in the gaps to complete the system of inequalities.
$x$x $\ge$≥ $\editable{}$
$y$y $\ge$≥ $\editable{}$
$x+y$x+y $\le$≤ $\editable{}$
Graph the system of inequalities.
Loading Graph...If $14$14 staff are allocated to checking in passengers of flight A, what is the maximum number of staff that can be allocated to checking in passengers of flight B?
Question 2
Applicants for a particular university are asked to sit a numeracy test and verbal reasoning test. Successful applicants must obtain a minimum score of $17$17 on a numeracy test and a minimum combined score of $37$37 for both tests.
Let $x$x and $y$y represent an applicant’s score on the numeracy and verbal reasoning test respectively.
State the system of inequalities on the same line, separated by a comma.
Create a graph of the system of inequalities.
Loading Graph...Which of the following points represents scores that would make the applicant successful?
$\left(14,16\right)$(14,16)
A$\left(33,18\right)$(33,18)
B$\left(20,13\right)$(20,13)
C$\left(12,38\right)$(12,38)
DIf an applicant obtains a score of $24$24 in the numeracy test, what is the minimum integer score they need to obtain in the verbal reasoning test to be successful?