Solve Linear Inequalities from a Graph

Previously, we learnt how to solve linear inequalities. Remember that a linear inequality in $x$x will not involve $x^2$x2, $x^3$x3, $\frac{1}{x}$1x​, or anything else. It will only ever involve $x$x being multiplied or divided by constants, or having constants added or subtracted.

In other words, the left hand side and right hand side of a linear equality will both be lines!

Think about it. If we have the linear inequality $3x-5<-5x+11$3x−5<−5x+11, the left hand side is the line $y_1=3x-5$y1​=3x−5 and the right hand side is the line $y_2=-5x+11$y2​=−5x+11.

We could solve the inequality algebraically like this.

$3x-5$3x−5	$<$<	$-5x+11$−5x+11
$8x-5$8x−5	$<$<	$11$11	Add $5x$5x to both sides
$8x$8x	$<$<	$16$16	Add $5$5 to both sides
$x$x	$<$<	$2$2	Divide both sides by $8$8.

Or, we could realise that to solve $3x-5<-5x+11$3x−5<−5x+11 we just need to find for what values of $x$x the line $y_1=3x-5$y1​=3x−5 is less than $y_2=-5x+11$y2​=−5x+11.

We can graph both lines like this.

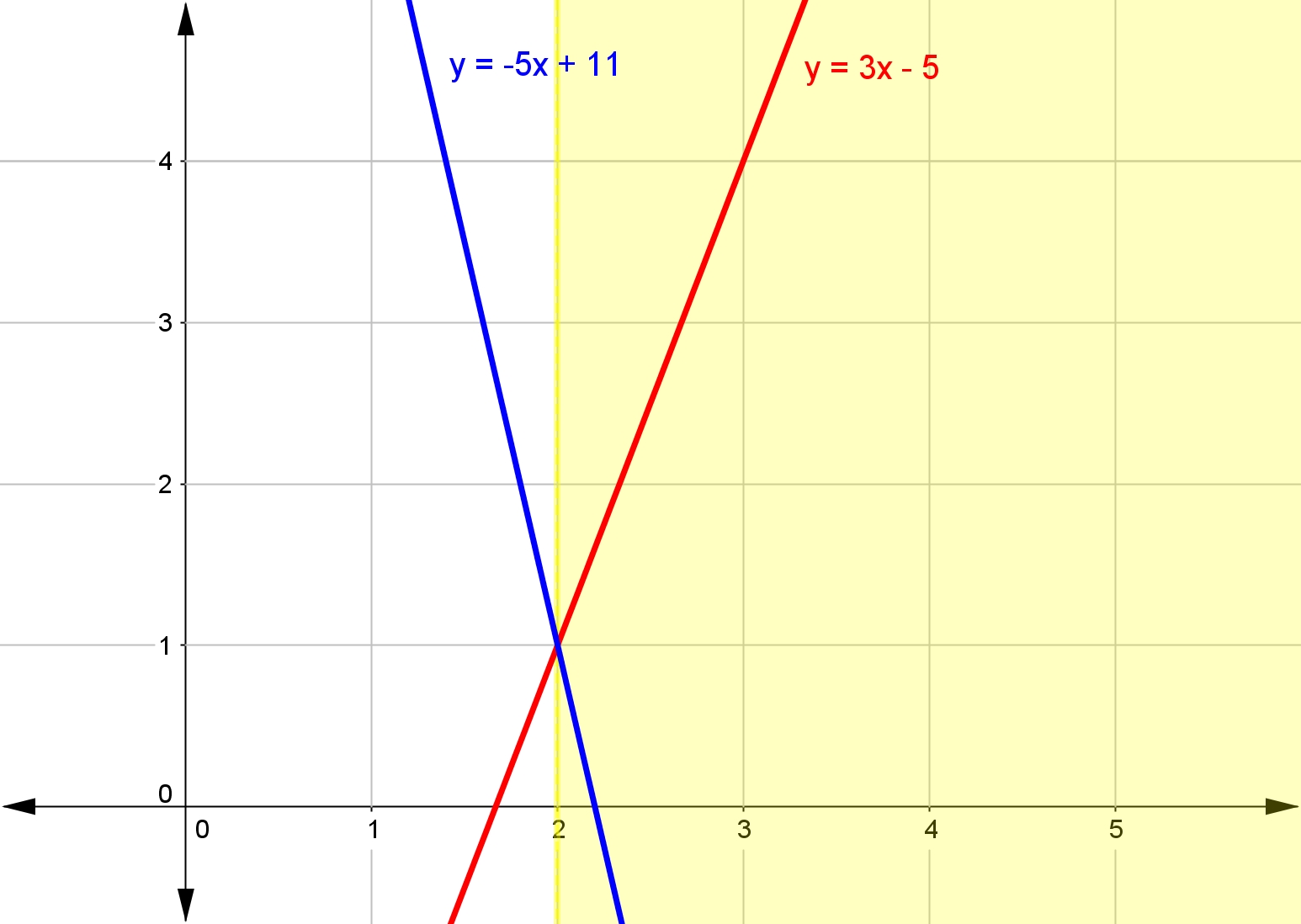
For what values of $x$x is the line $y_1=3x-5$y1​=3x−5 less than $y_2=-5x+11$y2​=−5x+11? In other words, when is the line $y_1=3x-5$y1​=3x−5 below the line $y_2=-5x+11$y2​=−5x+11?

Just as we found by solving the inequality algebraically, $y_1$y1​ is below $y_2$y2​ for $x<2$x<2.

Worked Examples

Question 1

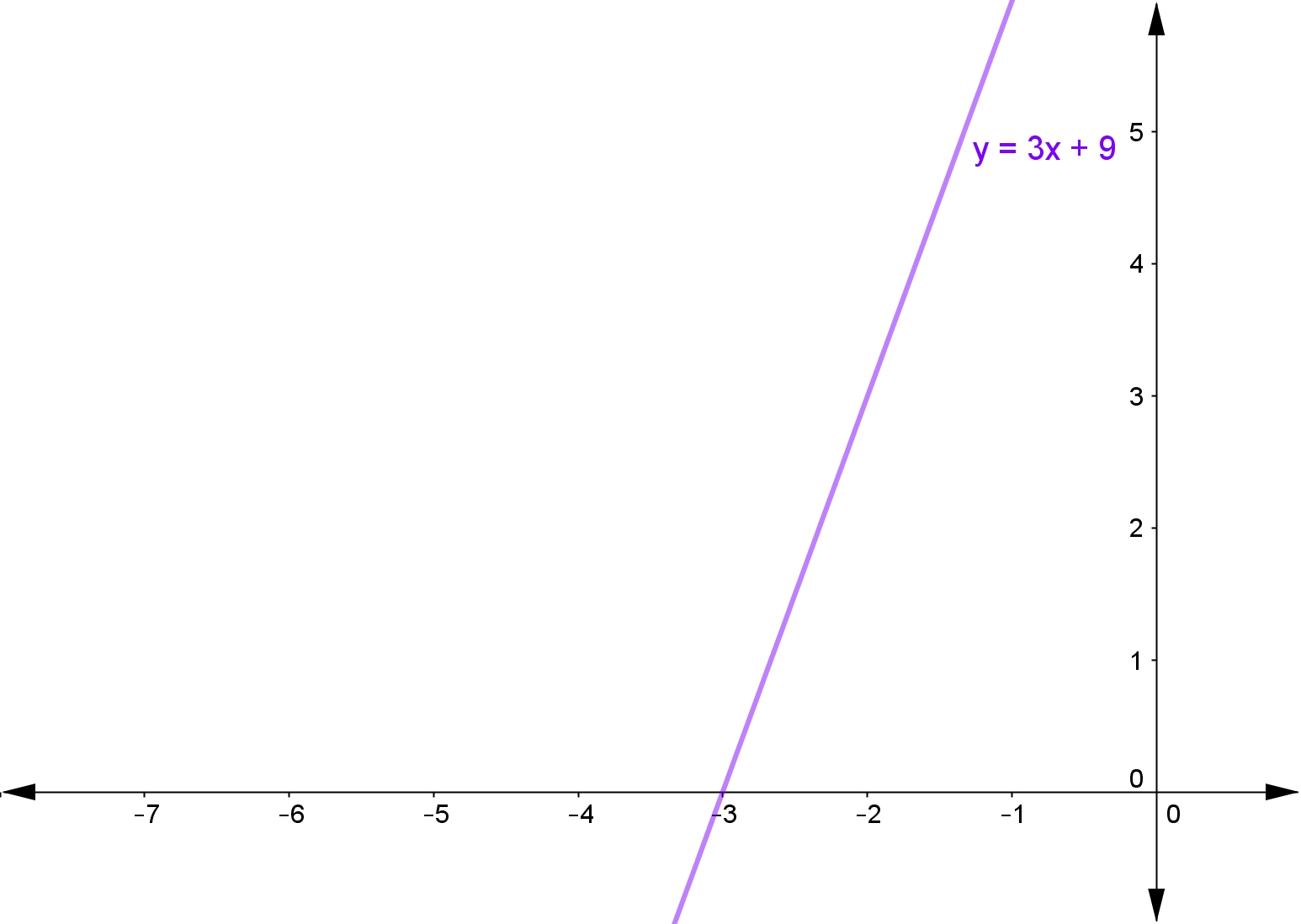
Using the above graph, state the solution to the linear inequality $3x+9\ge0$3x+9≥0 and plot the solution on a number line.

The solution to the inequality $3x+9\ge0$3x+9≥0 will be whenever the line $y=3x+9$y=3x+9 is above the line $y=0$y=0 (the $x$x-axis), in other words, when the line is positive.

We can see that this happens when $x\ge-3$x≥−3, which we can plot on the number line like this.

Question 2

Using the above graph, state the solution to the linear inequality $3x-21<9$3x−21<9 and plot the solution on a number line.

 

The solution to the inequality $3x-21<9$3x−21<9 will be whenever the line $y=3x-21$y=3x−21 is below the line $y=9$y=9.

We can see that this happens when $x<10$x<10, which we can plot on the number line like this.

 

Worked Examples

Question 1

Question 2

Question 3