Reducing Balance Loans
At some point in your life it's highly likely that you will take out a reducible balance loan.
This is the sort of loan where you are charged compound interest as your fee for borrowing money, and at regular time periods, usually months, you are required to make repayments to the financial institution to slowly pay off your loan.
As you pay a bit back each time period, the amount you owe, or the balance, reduces, hence the name of this style of loan.
The most common reducible balance loan type is a mortgage. This is when you borrow money to buy a property. Some people take out what is known as an interest-only loan where they pay back the interest each month, but none of what they borrowed. A financial institution usually only allows you to do this for a few years.
Analysing a Reducible Balance Loan with a Table
example
Mr and Mrs Roberts take out a mortgage to purchase a house. They borrow $\$550000$$550000 from a bank that charges them $5.8%$5.8% interest, compounded monthly. At the end of each month the Roberts make a repayment of $\$3500$$3500.
We can represent this situation using a spreadsheet. The first and last part of the loan is shown below.
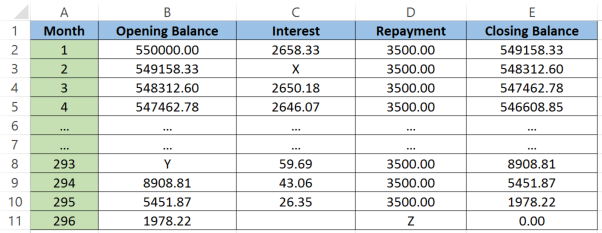
(a) Calculate the value of X in the table
Think: X is situated in the interest column, so we can use the information we have to calculate X.
Do:
$X=\frac{0.058}{12}\times549158.33$X=0.05812×549158.33
$X=2654.26$X=2654.26
(b) Calculate the value of Y in the table
Think: Usually finding the opening balance is easy because it's the same as the closing balance from the previous time period. But we can't see it in this case. So we'll need to work backwards.
Do:
$Y+56.59-3500=8908.81$Y+56.59−3500=8908.81
$Y=12349.12$Y=12349.12
(c) Calculate the value of Z in the table
Think: This is the month where the Roberts will crack open a bottle of Champagne since they've finally paid off their loan! Their final repayment will be less than their usual amount.
Do:
$Z=1978.22+\frac{0.058}{12}\times1978.22$Z=1978.22+0.05812×1978.22
$Z=1987.78$Z=1987.78
(d) Calculate the total repayments made by the Roberts
Think: The Roberts have made $295$295 repayments each of $\$3500$$3500 plus the final repayment of $\$1987.78$$1987.78
Do: Total repayments = $295\times3500+1987.78$295×3500+1987.78
Total repayments = $\$1034487.78$$1034487.78
(e) Hence determine the total interest the Roberts paid for the loan
Think: The total interest paid on the loan is their total repayments minus the amount they borrowed.
Do: $1034487.78-550000$1034487.78−550000=$\$484487.78$$484487.78
So you can see that they nearly paid double the purchase price over the $296$296 months, or $25$25 years.
You can see that this is a lot of money! Unless their house doubles in value over $25$25 years, the Roberts have paid more for their house than what it's worth. Could they prevent that?
They could try to do a combination of the following:
- Make fortnightly repayments. If they did so, they'd end up making an extra repayment each year since there are $26$26 fortnights in a year. $\frac{26}{2}=13$262=13 so it's like you've paid for $13$13 months instead of $12$12.
- Increase the amount they repay. Intuitively, if you make larger repayments each month or fortnight, you'll be able to pay off your loan sooner, saving you a lot of interest and thus helping you pay less overall.
Calculations using the CAS Financial Application
Creating and analysing a spreadsheet can be time consuming and often it's more convenient to analyse various situations for a reducible balance loan using the financial facility of our calculator. In fact, I recommend you remember all this for when you take out your first loan!
example
Audrey takes out a car loan for $\$24000$$24000. The finance company charge her $8.5%$8.5% interest compounded monthly. How much should Audrey repay each month if she wants to repay this loan in $5$5 years?
Using the financial application on our CAS we'd fill it in as follows:
l
I is our annual interest rate of $8.5%.$8.5%.
PV is the present value of our loan and it is $24000$24000 because from Audrey's point of view she has been given this money by the financial institution
PMT is what we want to find, that is, Audrey's payment amount
FV is the future value of the loan which of course Audrey wants it to be $0$0
P/Y is the number of payments or repayments made each year, which is $12$12
C/Y is the number of compounding periods each year, which is also $12$12
Solving we get:

So Audrey should pay $\$492.40$$492.40 each month. Note that here PMT displays as a negative number since the payments will be made from Audrey to the financial institution.
Worked Examples
Question 1
Ivan takes out a car loan for $\$24000$$24000. He is charged $8.1%$8.1% per annum interest, compounded monthly. Ivan makes repayments of $\$450$$450 at the end of each month.
Complete the values in the empty cells in the table below. Give your answers correct to the nearest cent.
Month Opening Balance Interest Repayment Closing Balance 1 $24000$24000 $162.00$162.00 $450$450 $23712.00$23712.00 2 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ 3 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$
Question 2
Mr. and Mrs. Dave have a mortgage.
The final months of their repayments are shown below.
Month Opening Balance Interest Repayment Closing Balance $146$146 $26452.84$26452.84 $198.40$198.40 $5000$5000 $21651.24$21651.24 $147$147 $21651.24$21651.24 $162.38$162.38 $5000$5000 $16813.62$16813.62 $148$148 $16813.62$16813.62 $126.10$126.10 $5000$5000 $11939.72$11939.72 $149$149 $11939.72$11939.72 $89.55$89.55 $5000$5000 $7029.27$7029.27 $150$150 $7029.27$7029.27 $52.72$52.72 $5000$5000 $2081.99$2081.99 Calculate the monthly interest rate charged on this loan. Give your answer as an percentage to two decimal places.
Complete the next row of the table, giving your answers correct to two decimal places.
Month Opening Balance Interest Repayment Closing Balance $146$146 $26452.84$26452.84 $198.40$198.40 $5000$5000 $21651.24$21651.24 $147$147 $21651.24$21651.24 $162.38$162.38 $5000$5000 $16813.62$16813.62 $148$148 $16813.62$16813.62 $126.10$126.10 $5000$5000 $11939.72$11939.72 $149$149 $11939.72$11939.72 $89.55$89.55 $5000$5000 $7029.27$7029.27 $150$150 $7029.27$7029.27 $52.72$52.72 $5000$5000 $2081.99$2081.99 $151$151 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ How many years did it take for them to pay off the loan?
Give your answer in the form of a mixed number.
Calculate the total repayments.
If they paid $\$302097.60$$302097.60 in interest, how much did they initially borrow?
Question 3
Mr and Mrs Gwen held a mortgage for $25$25 years. Over that time they made monthly repayments of $\$4500$$4500 and were charge a fixed interest rate of $4.4%$4.4% per annum, compounded monthly.
We will use the financial solver on your CAS calculator to determine how much they initially borrowed.
Which variable on the CAS calculator do we want to solve for?
PVAI%BNCPmtDFVEFill in the value for each of the following:
N:$\editable{}$I%:$\editable{}$Pmt:$\editable{}$FV:$\editable{}$PpY:$\editable{}$CpY:$\editable{}$Hence, state how much Mr. and Mrs. Gwen initially borrowed, correct to the nearest dollar.