Bearings
In surveying and air navigation, bearing are used to help identify the location of an object.
The four main directions of a compass are known as cardinal directions. They are north (N), east (E), south (S) and west (W).

Three-figure (True) Bearings
A three-figure bearing are:
- measured from north ($N$N)
- measured in a clockwise direction
- written using three figures
A $T$T is often but not always used to indicate a true bearing. If the angle measure is less than $100^\circ$100° it would be written something like 040° or 040°T.
To use true bearing to describe the location of a plane at point $B$B from the airport at point $A$A :
- place the centre of a compass on the starting point, in the case the airport.
- starting at North, rotate clockwise until we get to the line $AB$AB.
- write angle as the true bearing of point $B$B.

The true bearing of $B$B from $A$A is $127^\circ$127° or $127^\circ$127°$T$T.
The diagram below describes the bearing of $P$P from $O$O. Rotating clockwise from North, we get an angle of $55^\circ$55°.

Since this measure is less than three digits, we put a 0 in front of it so the true bearing of $P$P is 055°. Consider the true bearing of $O$O from $P$P . Since angle of elevation is equal to angle of depression and we are starting at $P$P the true bearing would be $180+55=235^\circ$180+55=235°.
Compass Bearings
A compass bearing describes the location of a point using:
- the starting direction of either north or south;
- the acute angle needed to rotate
- the direction to rotate, east or west.
To describe the position of point $B$B from $A$A we would say:
"Starting at South, I then rotate $53$53° towards East."
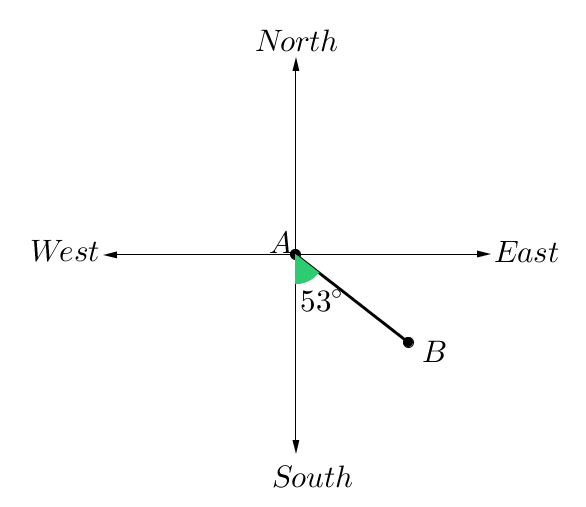
We can write this mathematically as:
$S$S$53$53°$E$E
Example
Find the three-figure and the compass bearings of point $P$P from $O$O.
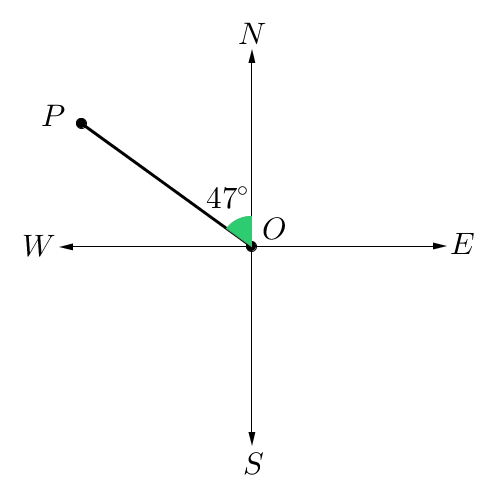
Solution:
Three-figure bearing:
Starting at North rotate in a clockwise direction.
$360^\circ-47^\circ=313^\circ$360°−47°=313°
The three-figure bearing of $P$P from $O$O is $313^\circ$313°$T$T.
Compass Bearing
Point $P$P is closest to North, so starting at North, rotate $47^\circ$47° towards West.
The compass bearing of $P$P from $O$O is $N$N$47^\circ$47°$W$W.
Which one first?
The bearing needed or used completely depends on which position comes first. Have a look at the investigation below, it quickly shows you how the angle changes depending on if we are measuring the bearing of A from B or B from A.
Let's have a look at these worked examples.
Question 1
Consider the point $A$A.

Find the true bearing of $A$A from $O$O.
What is the compass bearing of point $A$A from $O$O?
$\editable{}$ $\editable{}$$^\circ$° $\editable{}$
Question 2
What is the true bearing of Southwest?
Question 3
In the figure below, point $B$B is due East of point $A$A. We want to find the position of point $A$A relative to point $C$C.

Find the true bearing of point $A$A from point $C$C.
What is the compass bearing of point $A$A from point $C$C?
$\editable{}$ $\editable{}$$^\circ$° $\editable{}$