Operations with Mixed Numbers
Fractions pop up in so many different places everyday. We use fractions when dealing with decimals, percentages, rates, ratios, lengths, distances and so on. When figuring out anything from how much change we get at the shop to cutting a cake to simply measuring things, fractions play an important part in our understanding of how many parts anything can be divided into.
One aspect of fractions that might be a bit daunting is this idea of 'Mixed' numbers.
Proper fractions
A fraction is considered proper, if it is of the form $\frac{A}{B}$AB and $A
This means that if a fraction does not have this form it is either Mixed OR Improper.
Improper fractions
A fraction is called improper if the top number (numerator) is larger than the bottom number (denominator). That makes it of the form $\frac{A}{B}$AB where $A>B$A>B.
So the following are all improper fractions,
$\frac{45}{46}$4546, $\frac{110}{43}$11043, $\frac{7}{4}$74, $\frac{11}{3}$113 and so on.
Adding and subtracting improper fractions
Adding and subtracting improper fractions is exactly the same process as adding and subtracting other types of fractions like we did here in Adding Parts . It might look a little different and the numbers might get bigger than your used to, but it's all the same!
Examples
Question 1
Evaluate: $\frac{9}{4}+\frac{6}{5}$94+65
Think: Find the LCM between $4$4 and $5$5 and find equivalent fractions. Then we will be able to add them.
Do: The LCM between $4$4 and $5$5 is $20$20.
| $\frac{9}{4}+\frac{6}{5}$94+65 | $=$= | $\frac{45}{20}+\frac{24}{20}$4520+2420 |
| $=$= | $\frac{69}{20}$6920 |
Mixed numbers
A fraction is called a mixed number if it is a combination of whole numbers and fractions.
The following are examples of mixed numbers.
1 $\frac{2}{3}$23, 14$\frac{5}{7}$57, 14$\frac{3}{5}$35
Adding and subtracting mixed numbers
There are two ways of looking at adding or subtracting mixed numbers.
Method 1 - Using improper fractions
The first idea is to convert the mixed number into an improper fraction and then add or subtract as we do normally.
A number like this $1\frac{2}{3}$123 means $1$1 whole and $\frac{2}{3}$23. To turn this into an improper fraction you need to work out how many thirds there are in $1$1 whole and $\frac{2}{3}$23 altogether. Well there are $3$3 thirds in a whole, so altogether we have $5$5 thirds, $\frac{5}{3}$53.
$14\frac{5}{7}$1457 means $14$14 wholes and $\frac{5}{7}$57. To turn this into an improper fraction you need to work out how many sevenths there are altogether in $14$14wholes and $\frac{5}{7}$57. Well, $14$14wholes is $14\times7$14×7 sevenths, which is $98$98sevenths. Altogether then we have $98+5$98+5 sevenths which is $\frac{103}{7}$1037.
For any mixed number we can turn it into an improper fraction by thinking about it in this way.
Once it is in the form of an improper fraction you can add and subtract as we did before.

Converting a mixed numeral to an improper fraction
or more generally...

General form of converting to an improper fraction
Method 2 - Dealing with wholes and parts separately
Consider the question $2\frac{1}{5}+1\frac{1}{4}$215+114
What we have here is:
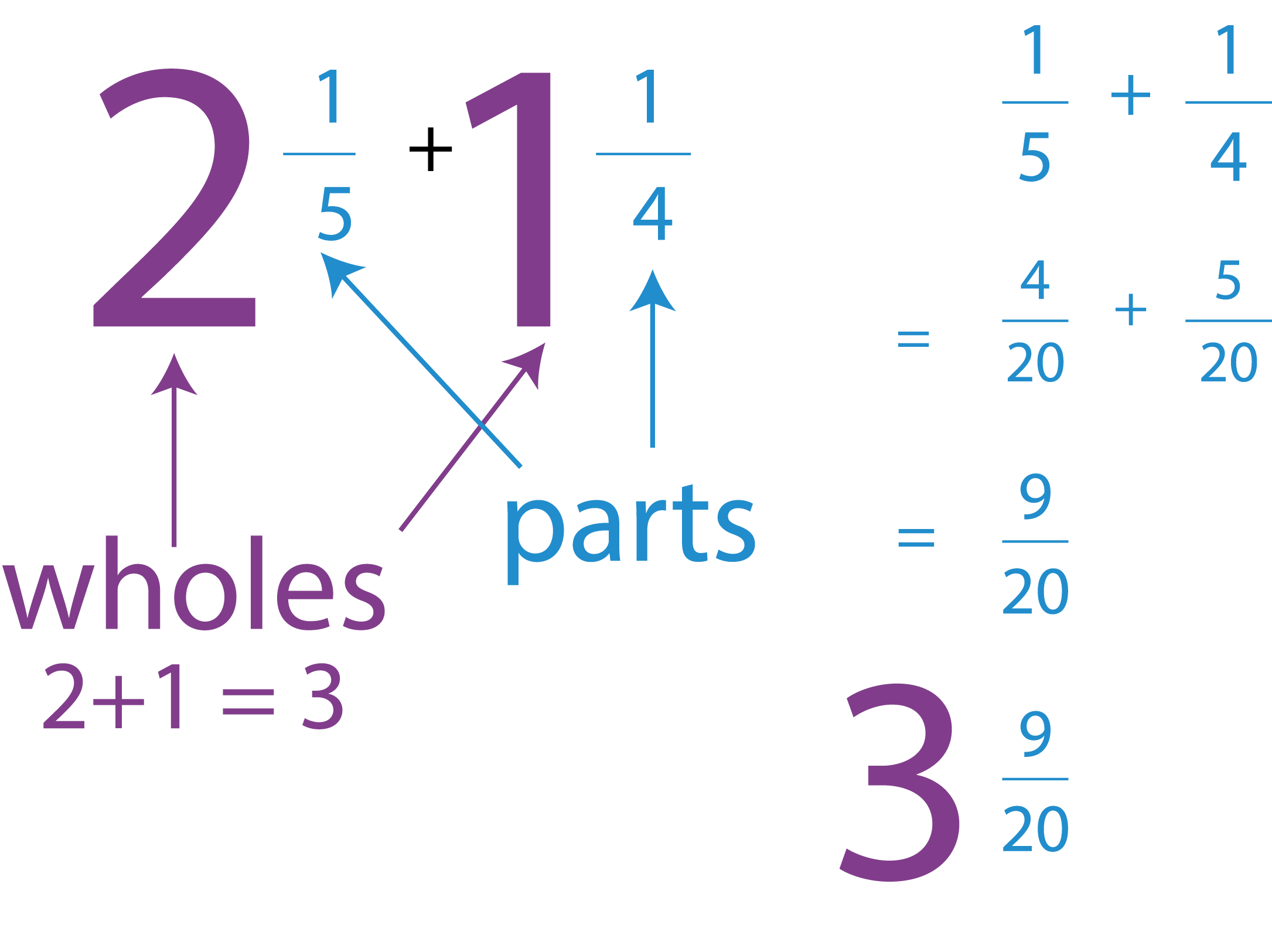
Question 2
Work out $9\frac{4}{19}+1\frac{3}{19}$9419+1319, leaving your answer as a mixed number.
Multiplication and division of mixed numbers
You may have noticed that the fractions we have multiplied so far were all less than or equal to 1. But how do we multiply fractions greater than 1? In particular, how do we multiply mixed numbers (combinations of whole numbers and fractions)?
For example, how do we multiply $1\frac{2}{3}$123 by $4\frac{5}{6}$456?
Multiplying with mixed numbers can be tackled via two different methods.
Method 1 - use improper fractions
Turn the mixed number into an improper one, and then multiply as normal.
Method 2 - multiply in parts
Separate the mixed number and multiply both parts. This seems like a more complicated method at first, but sometimes, especially if we have to work in our heads, it can be easier.
Lets consider this question, $2\frac{3}{5}\times\frac{3}{4}$235×34
a mixed number is an addition of 2 parts, the whole parts and the fractional part,

We can multiply the $\frac{3}{4}$34 by both the $2$2 and the $\frac{3}{5}$35
Complete the multiplications
and before we can add them we have to get a common denominator,
then add and simplify...
 =
= 
Which becomes the mixed number
Question 3
Evaluate $2\frac{2}{5}\times1\frac{3}{5}$225×135, giving your answer as a mixed number in simplest form.
Question 4
Evaluate $3\frac{2}{3}\div2\frac{1}{4}$323÷214, giving your answer as a mixed number in simplest form.




