Square and Cube Roots Using Factor trees
In Trees with Multiple Branches we discussed how prime factors can be used to find highest common factors and lowest common multiples. We can also use prime factors to find square and cube roots.
Let's look at factor tree and discuss how.
Square roots
question 1
Evaluate: $\sqrt{1444}$√1444
Think: Let's look for factors of $1444$1444 (it's most helpful if we can find numbers that make perfect squares).
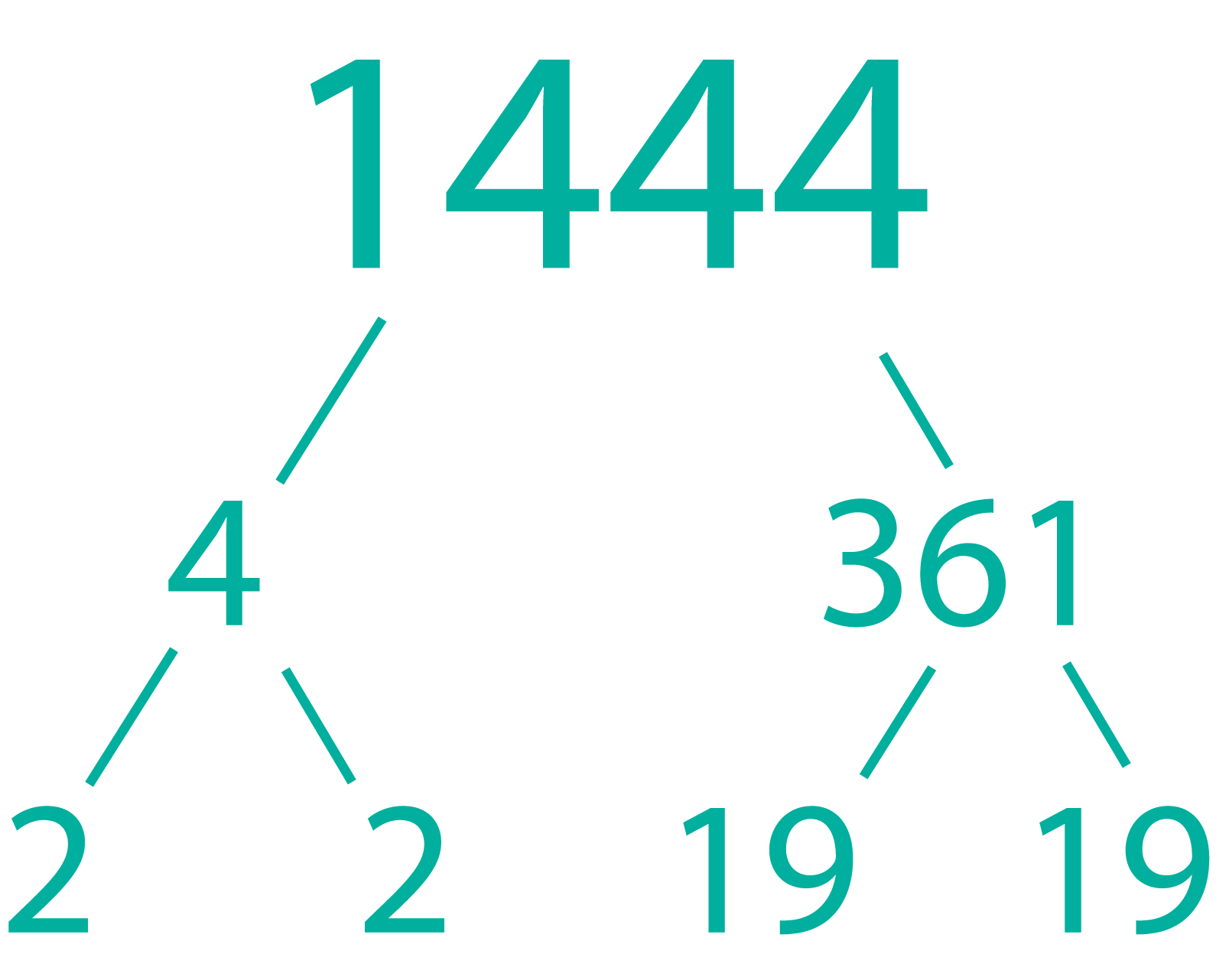
So $1444$1444 can be written as $2\times2\times19\times19$2×2×19×19. In index notation, we would write this as $2^2\times19^2$22×192
Do:
| $\sqrt{1444}$√1444 | $=$= | $2\times19$2×19 |
| $=$= | $38$38 |
Cube Roots
question 2
Evaluate: $\sqrt[3]{1728}$3√1728
Think:
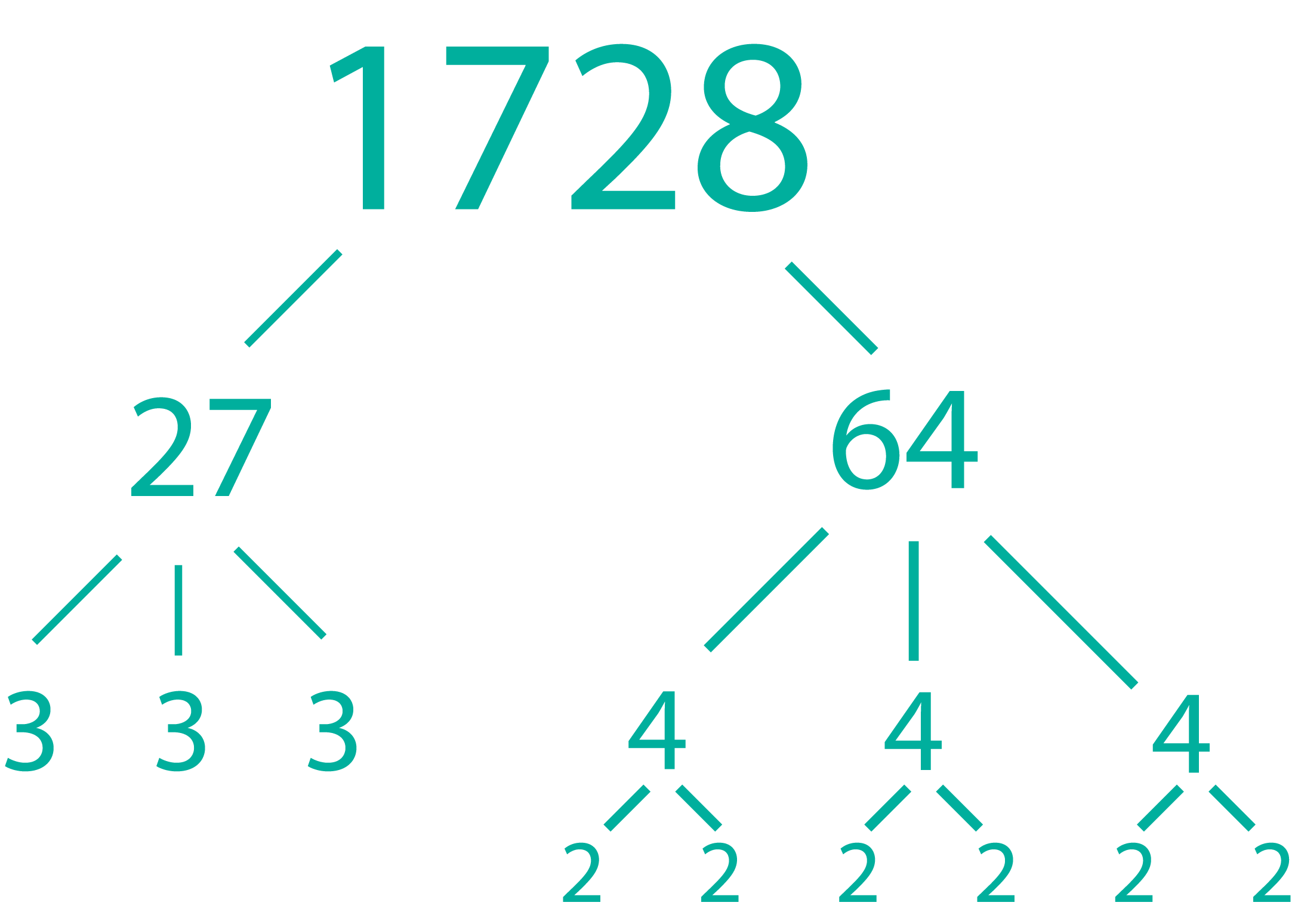
In index notation, we would write this as $3^3\times2^6$33×26
Since we need to find the cube root, we need to divide our groups of factors by $3$3.
Do:
| $\sqrt[3]{1728}$3√1728 | $=$= | $3\times2^2$3×22 |
| $=$= | $12$12 |
Worked Examples
Question 1
Use a factor tree to help find the $\sqrt{196}$√196
a) Write $196$196 as a product of prime factors in index notation.
b) Hence find the $\sqrt{196}$√196
Question 2
Given $85184=11^3\times2^6$85184=113×26
Find $\sqrt[3]{85184}$3√85184
Question 3
We want to find $\sqrt[3]{729}$3√729
a) Write $729$729 as the product of three identical
b) Hence evaluate $\sqrt[3]{729}$3√729