Types of Triangles

Are they the same?
To indicate if lines or angles have the same length or size we use identical markings.
We know for example that rectangles have opposite sides of equal length. We could indicate the equal lengths using identical markings like these.

Here we can see that the segments $AB$AB and $CD$CD are equal, similarly $AD$AD and $BC$BC are equal.
In a parallelogram we know that opposite sides are equal in length and parallel (you can see the equal in length markings on the sides) and we also know that opposite angles are equal in size. See how angle markings match to show they are the same.

From this picture we can see $\angle BAD=\angle BCD$∠BAD=∠BCD and $\angle ADC=\angle CBA$∠ADC=∠CBA, and that the segments $AB=DC$AB=DC and $AD=BC$AD=BC.
Types of triangles
There are a number of different types of triangles. The way we name them depends on specific properties relating to their side lengths or angles.
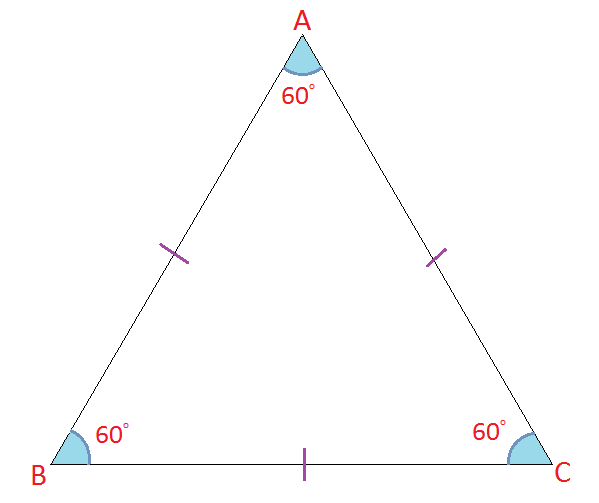
Equilateral triangles
An equilateral triangle has all side lengths equal (in this case $AB$AB$=$=$BC=CA$BC=CA) and all angles equal ($\angle ABC=\angle BCA$∠ABC=∠BCA$=$=$\angle CAB$∠CAB). Because all angles are the same, and there are $180$180° in a triangle, then each angle is $180\div3=60$180÷3=60°
Isosceles Triangles
An isosceles triangle has two sides of equal length and two equal angles.
The word isosceles comes from Greek, isos- meaning equal and celes - meaning legs. So isosceles means equal legs!
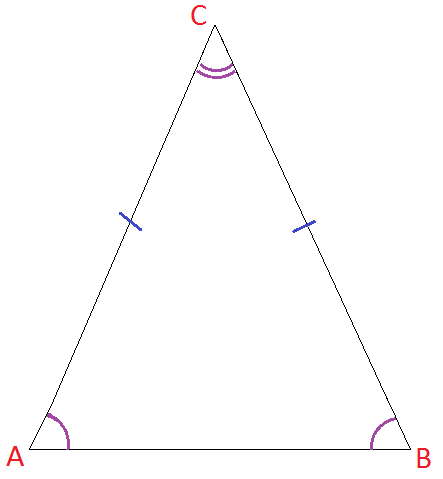
The equal angles in an isosceles triangle are called the base angles. Notice that the equal sides are always opposite to the base angles (more on that below).
Scalene Triangles
Scalene triangles are triangles that have 3 different length sides, they also have 3 different angles.

Side angle relationships
Something interesting to note about the relationship between sides and angles.
The biggest angle is always opposite the longest side and the smallest angle is always opposite the shortest side!
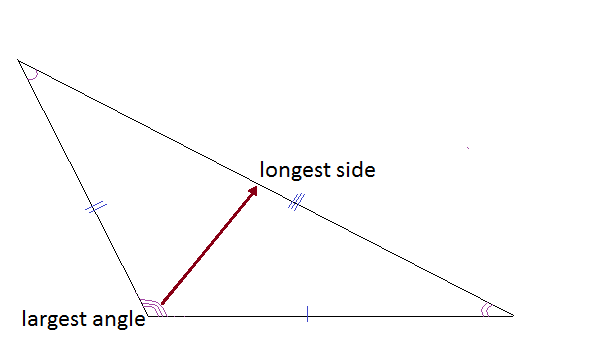
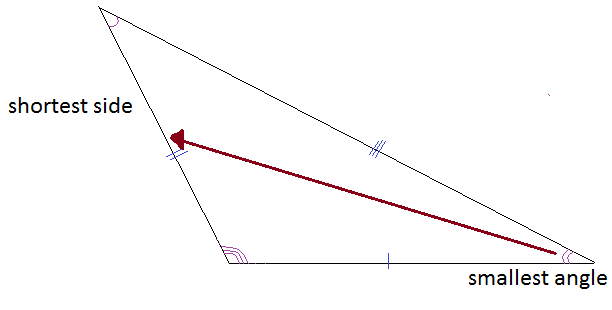
So if side lengths are equal, like in equilateral and isosceles triangles, then their corresponding opposite angles are also equal.
Right-angled triangles
Right-angled triangles have, as the name suggests, a right angle in them.
We can have scalene right-angled triangles, and isosceles right-angled triangles, but due to Pythagoras' theorem (that we will learn about later) we can never have an equilateral right-angled triangle. But you already knew that because equilateral triangles have all angles equal to 60° so they can't have a right angle.
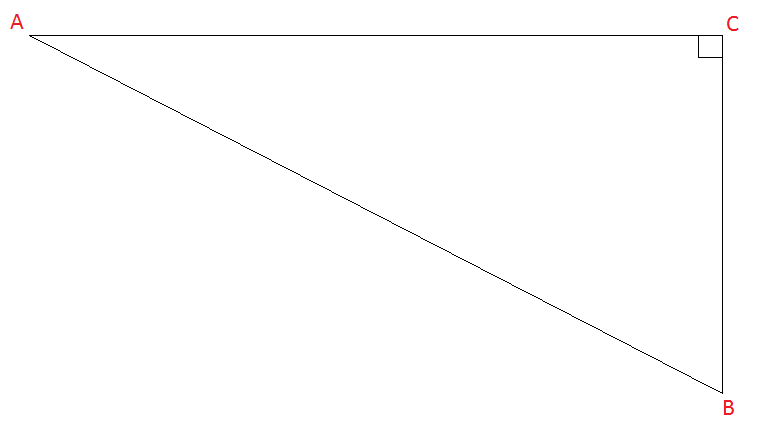

Intuitively we can see that if a triangle has an angle of $90^\circ$90°, then there cannot be another angle larger than or equal to that (because there's only $180^\circ$180° in a triangle), which means that the side opposite the right angle (called the hypotenuse) will always be the longest side in a right-angled triangle.
Acute and Obtuse
As we saw when we came across all the angle names, an acute angle is an angle
$<$< $90^\circ$90°, and an obtuse angle is an angle between $90^\circ$90° and $180^\circ$180°.
An acute triangle is a triangle, where all the angles are acute in size.
An obtuse triangle is a triangle, where one of the angles is obtuse in size.

Now that you've seen all the different ways to classify a triangle move point C in the interactive below to create as many different types of triangles as you can. Watch this video if you would like to see this interactive in action -
Worked Examples
Question 1
The following examples will show you how to classify different types of triangles.
Based on the length of the sides, choose the most appropriate classification for the triangles as scalene, isosceles, or equilateral.

A triangle with its dimensions labeled. The first side measures $10$10 cm, the second side measures $12$12 cm, and the third side measures $8$8 cm. Isosceles
AEquilateral
BScalene
C
An obtuse triangle with its dimensions labeled. The first and second side measures $7$7 cm, and the third side measures $9$9 cm. Isosceles
AScalene
BEquilateral
C
A right triangle with its dimensions labeled. The horizontal base of the triangle measures $12$12 cm. The vertical side measures $5$5 cm. And the hypotenuse measures $13$13 cm. Equilateral
AIsosceles
BScalene
C
A triangle with its dimensions labeled. All three sides are labeled to measure $10$10 m. Scalene
AEquilateral
BIsosceles
C
A triangle with its dimensions labeled. The first and second side measures $7$7 m, and the third side measures $9$9 m. Isosceles
AEquilateral
BScalene
C
A triangle with its dimensions labeled. All three sides are labeled to measure $7$7 m. Isosceles
AEquilateral
BScalene
C
Question 2
The route for a sailing regatta is planned out so that boats must travel $7$7 km North, then turn West and travel a further $10$10 km, before returning directly to the starting point.
What kind of triangle does the route border?
equilateral
Aright-angled
BObtuse
Cisosceles
D
Solving problems
When solving angle problems in geometry one of the most important components is the reasoning (or rules) you use to solve the problem. You will mostly be required in geometry problems to not only complete the mathematics associated with calculating angle or side lengths but also to state the reasons you have used. Read through each of these rules and see if you can describe why and draw a picture to represent it.
Properties of Triangles
| Angle sum of a triangle is 180° |  |
| Base angles are equal in an isosceles triangle
Sides opposite base angles are equal in an isosceles triangle |
 |
| All angles in an equilateral triangles are equal
All angles in an equilateral triangle are equal to 60° All sides in an equilateral triangle are equal |
 |
A summary of the geometry properties of angles can be found here.