The Number Plane (Q1 with symbols)
You may be able to find the place you live on a map but how would you describe it to somebody else on the other side of the world who didn't know where to find your town? Well, we can use a number plane to help us describe a position.
We can describe the position of any point using two values which are called a pair of coordinates.
Features of a Number Plane
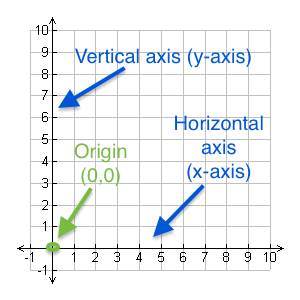
A number plane is made up of a horizontal and a vertical axis.
- The horizontal axis, called the$x$x-axis, is like a number line you have seen previously that runs from left the right.
- The vertical axis, called the $y$y-axis, is a number line that runs up and down.
- The two lines meet at the origin, which has coordinates $\left(0,0\right)$(0,0).
Let's look at an example of a number line now.
Reading and Writing Coordinates
Writing Coordinates
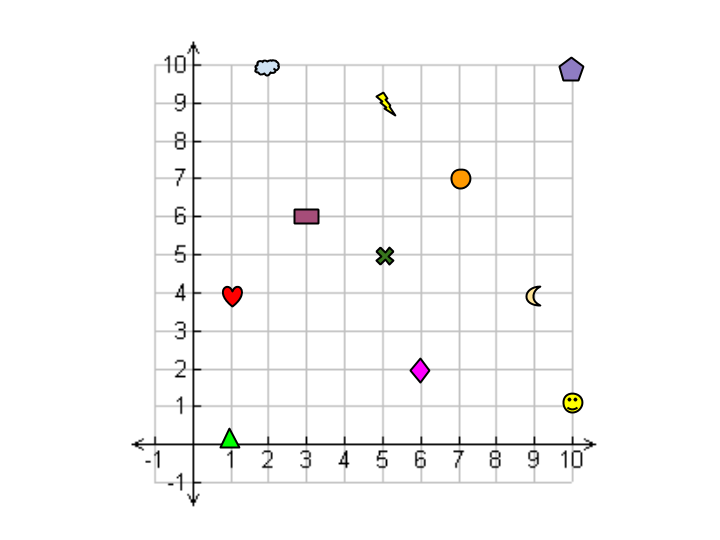
To write coordinates, we write the horizontal value, then the vertical value that a point is away from the origin. For example, in the picture below, the coordinates on the smiley face are $\left(10,1\right)$(10,1) because it is $10$10 units to the right of the origin and then $1$1 unit up.
Reading Coordinates
We read coordinates in the same way as we write them. Let's say I asked you what shape was at $\left(1,4\right)$(1,4). To work this out, you'd start at $\left(0,0\right)$(0,0), move $1$1 space to the right, then $4$4 spaces up. Where would you land? On the heart.
Plotting Points on a Plane
Now that we can read coordinates, we can plot (draw) the points on a number plane. Play with the applet below and practice plotting points.
Coordinates are written as:
(horizontal number, vertical number)
Worked Examples
Question 1
Here is a number plane.

What is at coordinate $\left(1,4\right)$(1,4)?
Heart
ACloud
BCircle
CSmiley face
DWhat is at coordinate $\left(10,1\right)$(10,1)?
Pentagon
ASmiley face
BCross
CRectangle
D
Question 2
Here is a number plane.

Write the coordinate of the circle.
$\left(\editable{},\editable{}\right)$(,)
Write the coordinate of the moon.
$\left(\editable{},\editable{}\right)$(,)
Question 3
Here is a number plane.

What is at coordinate $\left(6,2\right)$(6,2)?
Smiley face
ADiamond
BCloud
CCircle
DWrite the coordinate of the crown.
$\left(\editable{},\editable{}\right)$(,)