Multiplication x4

We've already discovered that doubling a number is the same as multiplying a number by 2.
So if we start with $1$1 group of $10$10, which contains $10$10 dots ($1\times10=10$1×10=10)

and we double it, we end up with $2$2 groups of $10$10. There are now $20$20 ($2\times10$2×10) dots.

How many groups would there be if we doubled the last answer?
Well, if we double $2$2 groups, there would now be $4$4 groups.
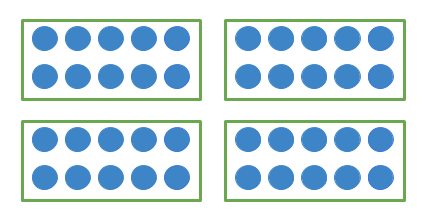
As we've doubled the number of groups, we can also double the number of dots. Double $20$20 is $40$40, so $4$4 groups of $10$10 or $4\times10=40$4×10=40.
The Double,Double Strategy
So as you can see, multiplying a number by $4$4 is the same as doubling the number, then doubling the answer. Watch this video to learn more about the double, double strategy.
Once you get confident using the double, double strategy, you can do it all in one step. This is a good thing to practice as most of the time on Mathspace, you need to enter all your marking in one step.
Let's look how:
What is $9\times4$9×4?
Think: We need to double $9$9, then double the answer. This is the same as $9\times2\times2$9×2×2.
| $9\times4$9×4 | $=$= | $9\times2\times2$9×2×2 | Double 9 is 18 |
| $=$= | $18\times2$18×2 | Now double 18 | |
| $=$= | $36$36 |
So $9\times4=36$9×4=36.
Of course, you don't have to use the double, double strategy. You may prefer to count up in groups of $4$4 and eventually, you may just know them so well that you don't even need to think about it! However, it's really good to understand what multiplying by $4$4 means, so you can eventually multiple really big numbers!
Let's have a look at some more examples now!
Worked Examples
Question 1
$4\times4$4×4
Question 2
$7\times4$7×4
Question 3
Use the double-double strategy to solve $4\times21$4×21.
First, evaluate $2\times21$2×21
Now, evaluate $2\times42$2×42
Hence, $4\times21$4×21