We’re going to jump right in here and investigate how the capitals of each Australian state and territory are connected by the road network. Here’s a map:

It’s hard to read the names of the cities, or even see where they are!
Now let’s draw the major roads connecting these cities together as undirected edges (since you can go back and forth along the roads!), and get rid of the state names:

I have added in three extra vertices (Katherine, Threeways, and Port Augusta) along the road from Adelaide to Darwin where it branches off to other cities. Without them we would have a single edge (road) connecting more than two vertices, which is not allowed.
Now we can get rid of the underlying map, and are left with the connections between the capital cities as a network:

If we only care about if we can get from one city to another, and not how far it is between the cities, we can simplify the network a lot:

We have converted the map to a network!
Now we can easily see all kinds of information:
- You can’t drive straight from Canberra to Perth without going through at least one other capital city along the way.
- If you’re in Hobart you can drive around but you’re never going to any other capital city.
- If you want to go from Melbourne to Sydney you can go through Canberra or you can drive around it.
And that's only the beginning! It’s not to scale anymore, but that’s ok - here we are only interested in whether cities are connected. Sometimes these sorts of rough networks are called mud maps, because they’re the kind of rough sketch that you can draw in the mud with a stick! Later on we will talk about ways to represent scale in networks.
You will see this kind of network all around you once you know how to look for it. For example, here is the London tube map as a network:
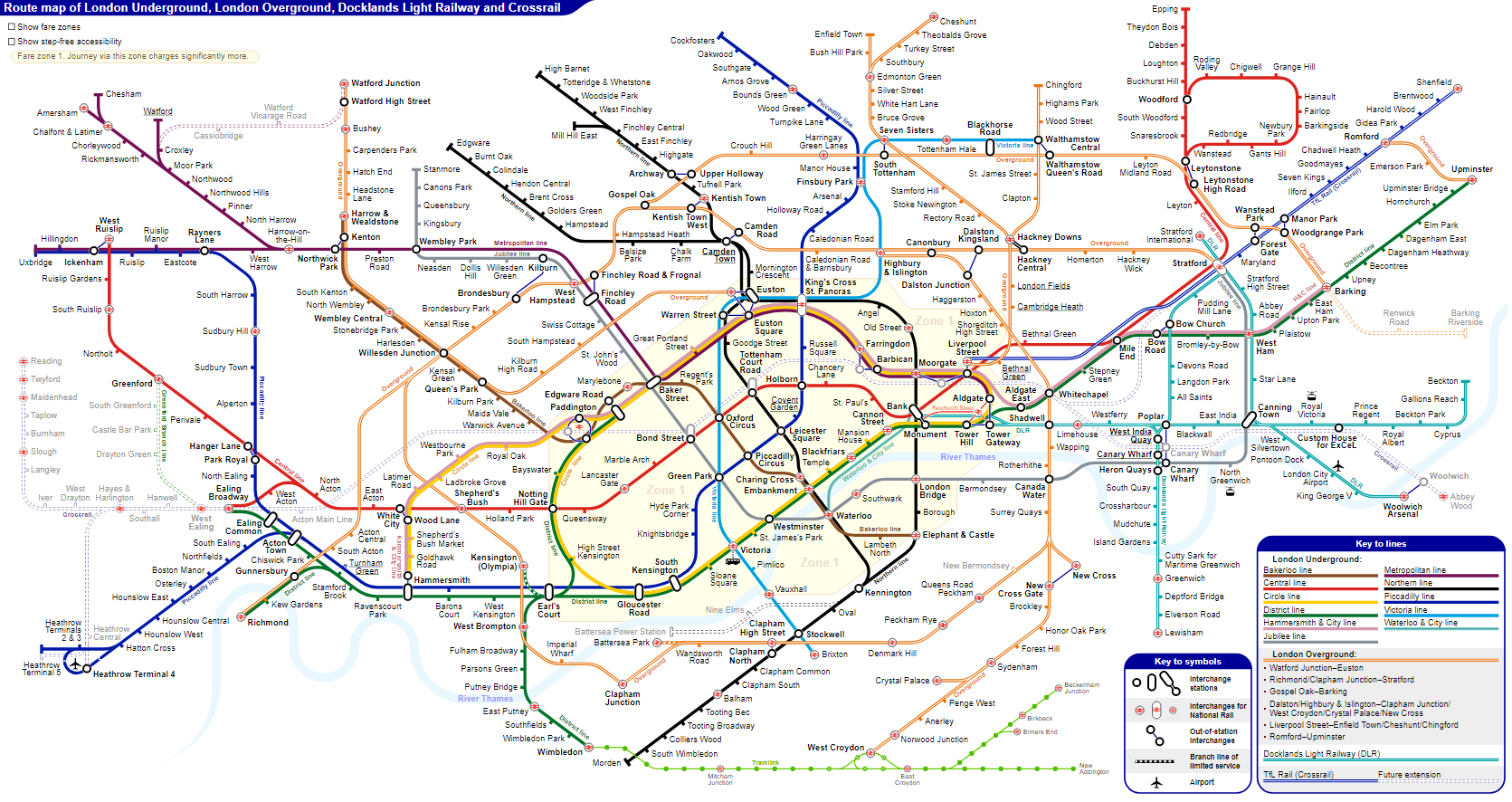
By sacrificing realism and only representing the information we care about (which stations are connected to which other stations and how), using the map becomes easier.
This next network is a completely different application. This is the family tree for King Charles II of Spain:
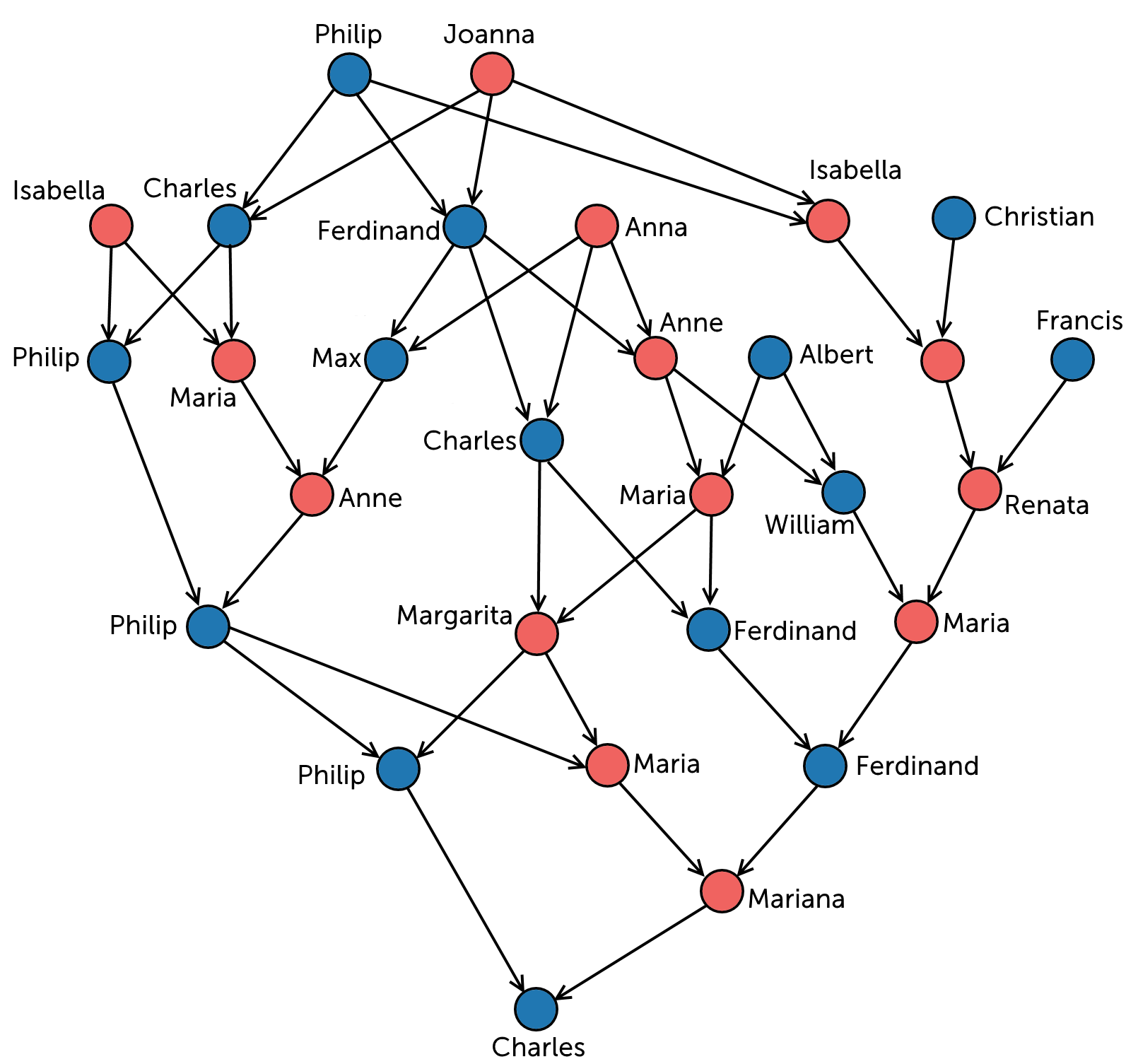
People used to think this was a good idea.
Note that the edges have arrows this time to show who is the parent and who is the child, so this is a directed network. There are seven vertices that don’t have any arrows pointing at them (can you find them all?), and every other vertex has exactly two edges pointing at them, one for their mother and one for their father. Try drawing out your own family tree as a directed network!
There are also times when we can represent the same idea two different ways. In this example, a small part of a city, containing seven blocks, needs to be serviced by a garbage collector. The garbage truck needs to travel along each side of each block.

If we replace every intersection with a vertex, we can use directed edges to represent the roads. The garbage truck then needs to travel along every edge to complete the route:

Or, we could replace each side of every road with a vertex, and connect the vertices with directed edges if we can travel from one to the other without making a right turn. The garbage truck then needs to travel to each vertex to complete the route:

Which one do you like best? Which one do you think is the most useful?