This chapter is about using the scale given on a map to calculate the actual distances between pairs of places.
Scale information is usually given in the form of a short line or bar whose length corresponds to a particular real distance. In the questions that go with this chapter, you will see that the scale bar is calibrated in both kilometres and miles. In some cases, you will need to check with a ruler to determine what units are assumed in the given information.
Example 1
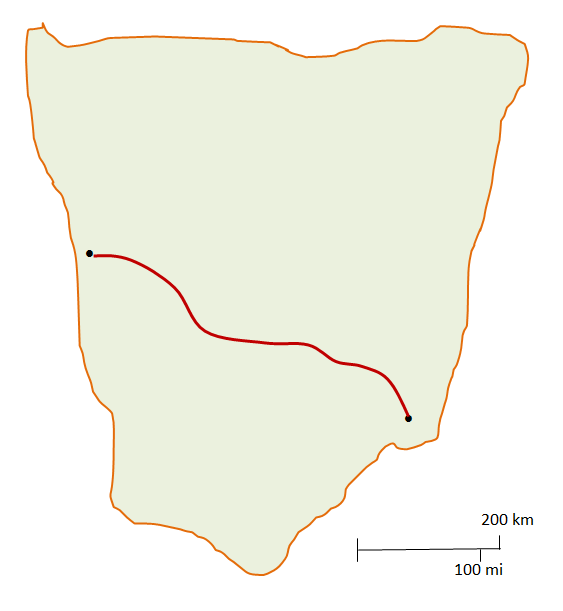
In this map, the distance between the two locations marked as black dots is approximately $2.5$2.5 of the $200$200-km scale units. This means the actual distance on the ground is $2.5\times200=500$2.5×200=500 km.
If, instead, we use the $100$100-mile scale unit, measurement with a ruler shows that there are roughly $3$3 of these units in the distance. Thus, in miles, the distance is $3\times100=300$3×100=300 miles.
Example 2
If a car travelling along the route shown in the map uses fuel at the rate of $8.1$8.1 litres per $100$100 km, how much fuel would be used for the one-way trip? At $$1.45$1.45 per litre, what would the cost be?
The distance $500$500 km is $5\times100$5×100. So, $5\times8.1=40.5$5×8.1=40.5 litres of fuel would be used. The cost is $1.45\times40.5=58.725$1.45×40.5=58.725 or just under $$60$60.
More Worked Examples
QUESTION 1
Ned took a plane from Brisbane to Townsville. The flight time was $2.4$2.4 hours. If the distance between Brisbane and Townsville is $5.8$5.8 units as it appears on the map, what is the average speed of the airplane?
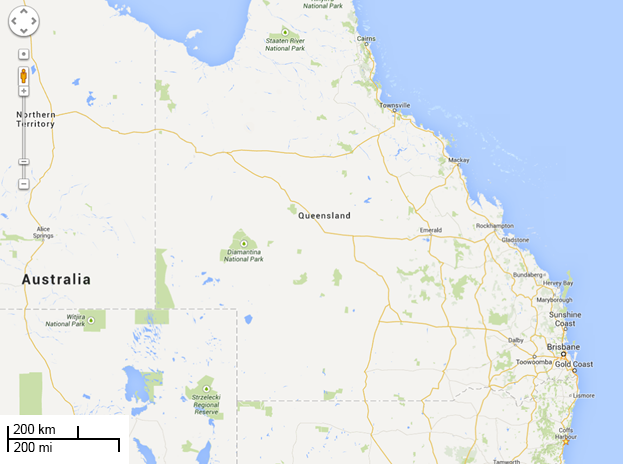
Evaluate the answer to two decimal places.
QUESTION 2
Using the map provided, which of the following distances is closest to the actual distance between Seoul and Tokyo?

$1499$1499km
A$1153$1153km
B$1038$1038km
C$922$922km
D