Topics
2. Quadratic Functions
topic badge
United States of AmericaVirginia
Algebra 2

2.07 Linear-quadratic systems

Lesson
Practice

Linear-quadratic systems

Exploration

Consider the following linear-quadratic system of equations:\begin{cases} y = 2x + 5 \\ y = x^{2} + 3x - 2 \end{cases}

  1. How could you use the substitution method to solve the system of equations?
  2. How could you use the elimination method to solve the system of equations?

A system of equations is a set of equations that have the same variables. We can apply the same algebraic methods for solving linear systems to non-linear systems. The goal is to create a one-variable equation so we can solve for that variable and use substitution to solve for the other.

We can go back and forth between representing systems of equations as a system, or as one equation, depending on the solution method we prefer to use. Consider the following equation:

\displaystyle 2x-3\displaystyle =\displaystyle x^{2}-x+4

This can be rewritten as:\begin{cases} y = 2x - 3 \\ y = x^{2} - x +4 \end{cases}

The solution to a system of equations is any ordered pair that makes all of the equations in the system true. For graphs, this will be all points of intersection. Solutions can be found algebraically or graphically.

x
y
The line and parabola have no points of intersection, so the system has no solution.
x
y
The line and parabola have one point of intersection, so the system has one solution.
x
y
The line and parabola have two points of intersection, so the system has two solutions.
x
y
The parabolas have two points of intersection, so the system has two solutions.
x
y
The parabolas have one point of intersection, so the system has one solution.
x
y
The parabolas do not have any points of intersection, so the system has no solution.
-4
-3
-2
-1
1
2
3
4
x
-6
-5
-4
-3
-2
-1
1
2
y

When the two quadratic equations in a system are equivalent, the parabolas will lie on top of one another when graphed. For example, the graphed system is \begin{cases}y=x^{2}-x-6\\ y=\left(x-3\right)\left(x+2\right)\end{cases}

This means all points on the parabolas will make both equations true. Since there are infinitely many points that lie on the parabolas, there are an infinite number of solutions.

The solution to a system of equations in a given context is viable if the solution makes sense in the context and is non-viable if it does not make sense.

Examples

Example 1

Consider the following systems of equations:

\begin{cases} y= x^{2} - 2 x - 3 \\ y= - x + 3 \end{cases}

a

Graph the equations on the same coordinate plane.

Worked Solution
Create a strategy

The solution(s) to a system of equations can be represented graphically as their point(s) of intersection. We can use technology to graph the two equations, or, if drawing them by hand, it will be useful to first fill out a table of values for both equations. We can use what we know about function types to pick the best range of table values. For example, we know the vertex of the quadratic equation will be at x = \dfrac{2}{\left(2\right)\left(1\right)} so we will want to choose x-cordinates on either side of x=1.

x-3-2-101234
y=x^{2} - 2 x - 31250-3-4-305
x-3-2-101234
y=-x+36543210-1
Apply the idea
-5
-4
-3
-2
-1
1
2
3
4
5
x
-5
-4
-3
-2
-1
1
2
3
4
5
y
Reflect and check

Notice that from the table of values both functions have the points \left(-2,5\right) and \left(3,0\right). We want these points of intersection to be visible on our graph. We also want the vertex of the parabola, \left(1,-4\right), to be visible.

We want to ensure that the x-values on our graph cover at least the interval -3 \leq x \leq 4 and the y-values on our graph cover at least the interval -5 \leq y \leq 6.

b

Identify the coordinates of the solution(s) to the system of equations.

Worked Solution
Apply the idea

The points of intersection occur at \left(-2, 5\right) and \left(3, 0\right). When creating the table, we saw that these values made both equations true, so these coordinate pairs are the solutions to the system of equations.

Reflect and check

Alternatively, we could have solved the system of equations algebraically, by equating both equations and solving for x.

\displaystyle y \displaystyle =\displaystyle x^{2}-2x-3First equation
\displaystyle -x+3\displaystyle =\displaystyle x^{2}-2x-3 Substitute y=-x+3
\displaystyle 3\displaystyle =\displaystyle x^{2}-x-3Add x to both sides
\displaystyle 0\displaystyle =\displaystyle x^{2}-x-6Subtract 3 from both sides
\displaystyle 0\displaystyle =\displaystyle \left(x+2\right)\left(x-3\right)Factor the quadratic

Using the zero product property, we can see the two solutions to this new quadratic are x=-2 and x=3.

We can now substitute these into one of the given equations to find the corresponding y-values.

\displaystyle y\displaystyle =\displaystyle -x+3Equation 2
\displaystyle =\displaystyle -\left(-2\right)+3Substitute x=-2
\displaystyle =\displaystyle 2+3Evaluate the multiplication of the signs
\displaystyle =\displaystyle 5Evaluate the addition

This corresponds with the solution \left(-2,5\right).

\displaystyle y\displaystyle =\displaystyle -\left(3\right)+3Substitute x=3 into Equation 1
\displaystyle =\displaystyle 0Evaluate the addition

This corresponds with the solution \left(3,0\right).

Example 2

Consider the quadratic-quadratic system of equations:\begin{cases} y=-2x^{2}+4 \\ y=x^{2}-4x+5 \end{cases}

a

Determine the number of solutions to the system of equations.

Worked Solution
Create a strategy

To determine the number of solutions to the system of equations, we can graph the system on a coordinate plane and look for points of intersection.

Apply the idea
-2
-1
1
2
3
4
x
-2
-1
1
2
3
4
y

From the graph, we can see that the parabolas intersect in two places.

Therefore, there are 2 solutions to the system of equations.

b

Find the solution(s) to the system of equations.

Worked Solution
Create a strategy

From the graph, we see that one of the solutions is \left(1,2\right) but the other solution does not have integer coordinates. For this reason, we must use technology to estimate the coordinates of the other point or solve algebraically.

When solving algebraically, using the substitution method is usually easiest, but the elimination method is also valid.

Apply the idea

Let's begin by numbering the equations to make them easier to work with.

1\displaystyle y\displaystyle =\displaystyle -2x^{2} + 4
2\displaystyle y\displaystyle =\displaystyle x^{2}-4x+5

Since both equations already have y isolated, we can start by substituting equation 1 into equation 2 to eliminate y from the equation.

\displaystyle y\displaystyle =\displaystyle x^{2}-4x+5Equation 2
\displaystyle -2x^{2}+4\displaystyle =\displaystyle x^{2}-4x+5Substitute y=-2x^{2}+4
\displaystyle 4\displaystyle =\displaystyle 3x^{2}-4x+5Add 2x^{2} to both sides
\displaystyle 0\displaystyle =\displaystyle 3x^{2}-4x+1Subtract 4 from both sides
\displaystyle 0\displaystyle =\displaystyle \left(3x-1\right)\left(x-1\right)Factor the quadratic

Now, we can solve for x using the zero product property.

\displaystyle 3x-1\displaystyle =\displaystyle 0Set the first factor equal to 0
\displaystyle 3x\displaystyle =\displaystyle 1Add 1 to both sides
\displaystyle x\displaystyle =\displaystyle \frac{1}{3}Divide both sides by 3
\displaystyle x-1\displaystyle =\displaystyle 0Set the second factor equal to 0
\displaystyle x\displaystyle =\displaystyle 1Add 1 to both sides

Finally, we will substitute the x-values back into one of the equations to solve for y.

\displaystyle y\displaystyle =\displaystyle -2x^{2}+4Equation 1
\displaystyle y\displaystyle =\displaystyle -2\left(\frac{1}{3}\right)^{2}+4Substitute x=\dfrac{1}{3}
\displaystyle =\displaystyle -\frac{2}{9}+4Evaluate the multiplication
\displaystyle =\displaystyle -\frac{2}{9}+\frac{36}{9}Rewrite with a common denominator
\displaystyle =\displaystyle \frac{34}{9}Evaluate the addition
\displaystyle y\displaystyle =\displaystyle -2\left(1\right)^{2}+4Substitute x=1
\displaystyle =\displaystyle -2+4Evaluate the multiplication
\displaystyle =\displaystyle 2Evaluate the addition

The solutions to the system are \left(\dfrac{1}{3},\dfrac{34}{9}\right) and \left(1,2\right).

Reflect and check

We can verify these solutions with technology or by substituting the values back into the equations to see if the solutions make both equations true.

Since we solved the system algebraically, we will check the answer by graphing with technology and using the tracing tool.

-2
-1
1
2
3
4
x
-2
-1
1
2
3
4
y

When the coordinates of the point are not integers or are rational numbers with more than 3 decimal place values, the calculator will give an approximation (a rounded estimate) of the values.

Note that \begin{aligned}\dfrac{1}{3}&\approx 0.333\\ \dfrac{34}{9}&\approx 3.778\end{aligned} which shows that our solutions are correct.

Example 3

Find the solution(s) for the following linear-quadratic system of equations:\begin{cases} y = 3 x + 1 \\ y = x^{2} - 5x \end{cases}

Worked Solution
Create a strategy

We can approach this graphically or algebraically.

-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
-5
5
10
15
20
25
y

But we can see from the graph that the points of intersection are not clearly identifiable. In cases like this, an algebraic approach is preferable. As both equations are already in terms of y, we can use the substitution method to solve.

Apply the idea
\displaystyle y \displaystyle =\displaystyle x^{2}-5xSecond equation
\displaystyle 3x+1 \displaystyle =\displaystyle x^{2}-5xSubstitute y=3x+1
\displaystyle 1\displaystyle =\displaystyle x^{2}-8xSubtract 3x from both sides
\displaystyle 0\displaystyle =\displaystyle x^{2}-8x-1Subtract 1 from both sides

This equation is not easily factorable, so we will use the quadratic formula to find the solutions.

\displaystyle x\displaystyle =\displaystyle \frac{-b\pm \sqrt{b^{2}-4ac}}{2a}Quadratic formula
\displaystyle =\displaystyle \frac{-\left(-8 \right) \pm \sqrt{\left(-8\right)^{2}-4\left(1 \right)\left(-1\right)}}{2\left( 1\right)}Substitute a=1, b=-8, c=-1
\displaystyle =\displaystyle \frac{8\pm \sqrt{64+4}}{2}Evaluate the square and products
\displaystyle =\displaystyle \frac{8\pm \sqrt{68}}{2}Evaluate the sum in the radicand
\displaystyle =\displaystyle \frac{8\pm 2\sqrt{17}}{2}Simplify the radical
\displaystyle =\displaystyle \frac{8}{2}\pm \frac{2\sqrt{17}}{2}Rewrite as two fractions
\displaystyle =\displaystyle 4\pm \sqrt{17}Simplify the quotients

We have found the x-coordinates of the points of intersection. We can substitute these into either equation to find the corresponding y-coordinate.

\displaystyle y\displaystyle =\displaystyle 3x+1
\displaystyle y\displaystyle =\displaystyle 3\left(4-\sqrt{17}\right)+1
\displaystyle y\displaystyle =\displaystyle 13-3\sqrt{17}

So one solution is \left(4-\sqrt{17}, 13-3\sqrt{17}\right), and using the same method, we find the other solution is \left(4+\sqrt{17}, 13+3\sqrt{17}\right).

Example 4

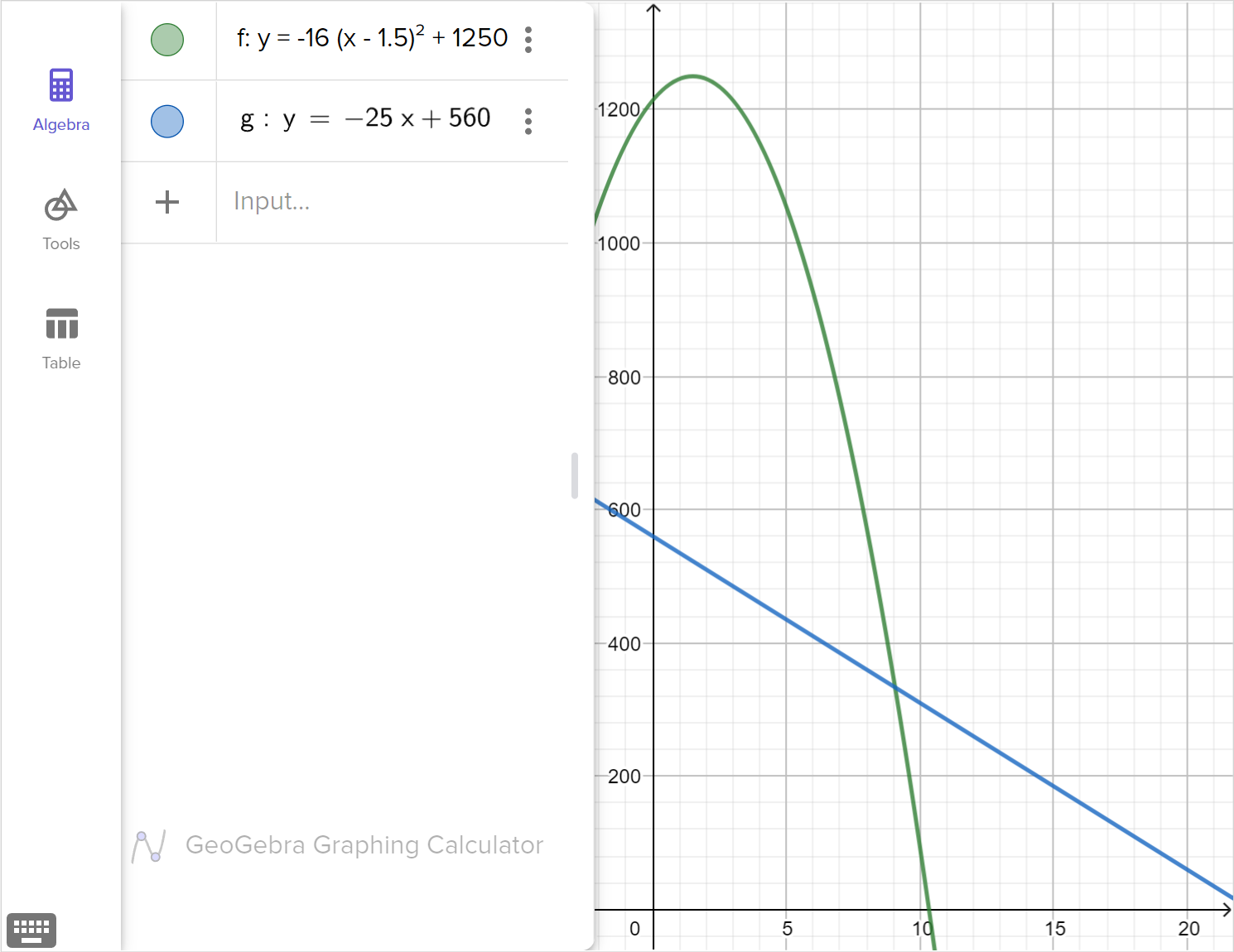
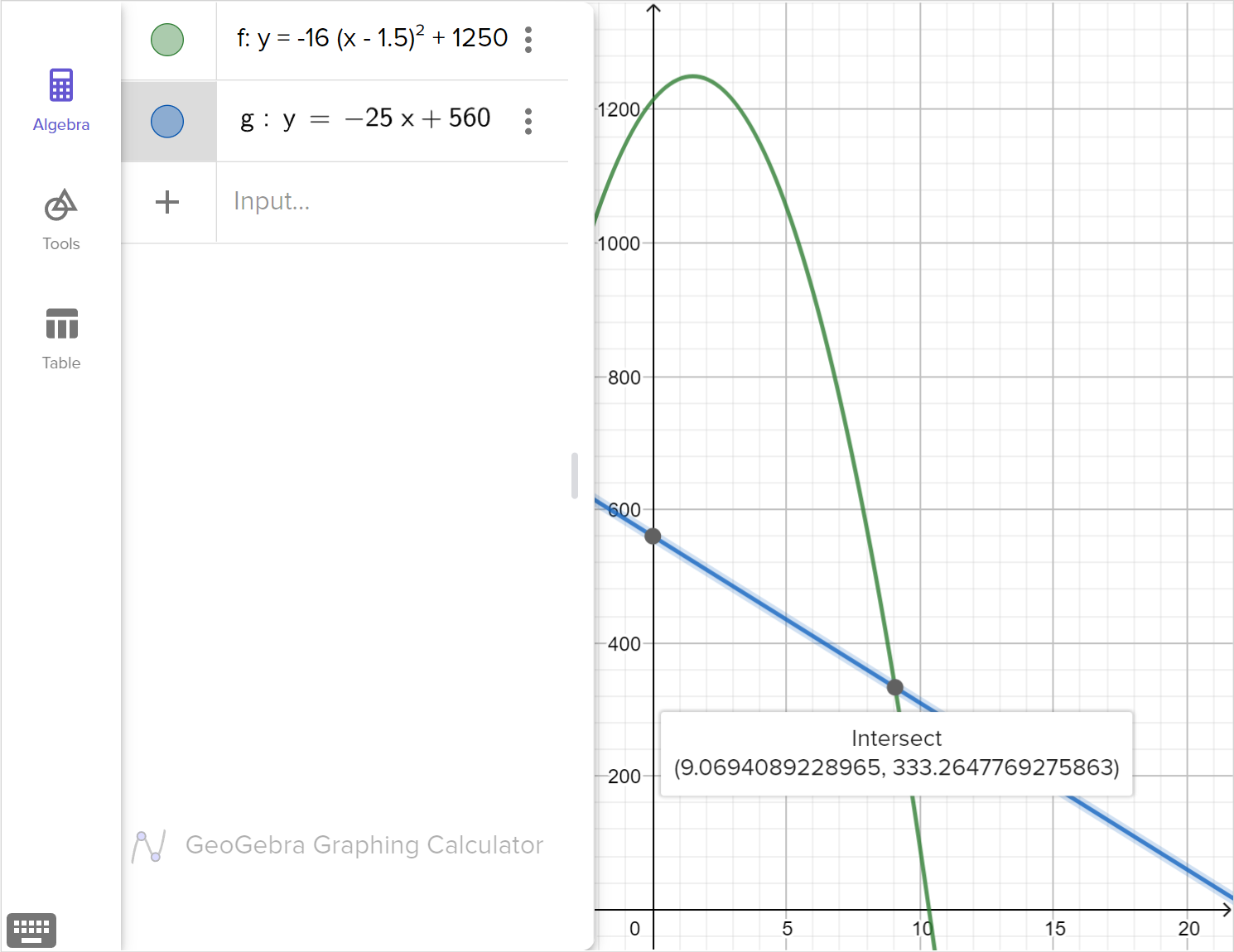
A base jumper jumps from the bridge of the Petronas towers, 560 ft high, immediately deploys his parachute, and then descends at a constant rate. At the same time, a ball is thrown from the observation deck of the tower, 1214 ft feet high and falls under gravity. Their height, y, after x seconds, is given by:

  • Base jumper: y=-25x+560

  • Ball: y=-16\left(x-1.5\right)^{2}+1250

a

Graph the height of the base jumper and ball on the same coordinate plane.

Worked Solution
Create a strategy

We can use technology to obtain a graph of the two functions, using the context and graphs to identify an appropriate domain and range for the graph.

Alternatively, we can graph by hand using key features of the graph such as:

  • The equation for the base jumper's height is a linear function, so we can identify the y-intercept, find another point on the line using the slope, and then graph the line through those two points.

  • The equation for the ball is in vertex form, so we can see the direction of opening from the coefficient, plot the vertex, then plot the y-intercept of \left(0,1214\right), and substitute another value for x to get the shape.

Apply the idea
Height over time
5
10
15
20
x \text{ (seconds)}
200
400
600
800
1000
1200
y \text{ (feet)}
Reflect and check

Consider what domain is appropriate for each graph in the context. The graphs should not extend beyond their valid domain.

b

Determine the time the base jumper and ball are at the same height.

Worked Solution
Create a strategy

Let's use technology to solve this problem. We can start by inputting the two equations for the base jumper and ball into a graphing calculator. We already have a sketch, so know we should end up with a parabola and a line.

A screenshot of the Geogebra Graphing Calculator showing the graphs of the functions y equals negative 16 quantity x minus 1.5 squared plus 1,250, and y equals negative 25 x plus 560. Speak to your teacher for more details.

We can estimate the coordinates by eye, but we should determine the coordinates more precisely using an intersection tool.

Apply the idea

From the graph, we can see that the graphs intersect at a single point in the domain appropriate to the context. To find the coordinates of this point, we can use the intersection tool. For the built-in GeoGebra graphing calculator, we need to click on the point of intersection.

A screenshot of the Geogebra Graphing Calculator showing the graphs of the functions y equals negative 16 quantity x minus 1.5 squared plus 1,250, and y equals negative 25 x plus 560. One of the points of intersection is highlighted. Speak to your teacher for more details.

The point where the graphs intersect within the restricted domain of the context is:\left(9.07, 333.26\right).

So, the ball and base jumper will be at the same height of approximately 333.26 ft at 9.07 seconds after the throw/jump.

Reflect and check

We can confirm this algebraically as well:

\displaystyle y\displaystyle =\displaystyle -25x+560First equation
\displaystyle -16\left(x-1.5\right)^{2}+1250\displaystyle =\displaystyle -25x+560Substitute y=-16\left(x-1.5\right)^{2}+1250
\displaystyle -16x^{2}+48x+1214\displaystyle =\displaystyle -25x+560Square the binomial and combine like terms
\displaystyle -16x^{2}+73x+654\displaystyle =\displaystyle 0Add 25x and subtract 560 from both sides

The solutions of this quadratic equation would give us the x-coordinates for any points of intersection between the two graphs.

The discriminant of this equation is \left(73\right)^{2}-4 \cdot \left(-16\right) \cdot 654=47\,185 \gt 0 which means there are two real solutions.

We could then use the quadratic formula to get the x-values of the points of intersection, ignoring negative solutions for this context.

Idea summary

A linear-quadratic or quadratic-quadratic system can be solved using the graphing method or substitution method. Using the graph is best when the intersection point(s) are clearly visible. Otherwise, solving the system algebraically or using an intersection tool with technology will lead to a more precise solution.

Outcomes

A2.EI.3

The student will solve a system of equations in two variables containing a quadratic expression.

A2.EI.3a

Create a linear-quadratic or quadratic-quadratic system of equations to model a contextual situation.

A2.EI.3b

Determine the number of solutions to a linear-quadratic and quadratic-quadratic system of equations in two variables.

A2.EI.3c

Solve a linear-quadratic and quadratic-quadratic system of equations algebraically and graphically, including situations in context.

A2.EI.3d

Verify possible solution(s) to linear-quadratic or quadratic-quadratic system of equations algebraically, graphically, and with technology to justify the reasonableness of answer(s). Explain the solution method and interpret solutions for problems given in context.

What is Mathspace

About Mathspace