6.07 Modeling with rational functions (M)
Introduction
In lesson 4.04 Modeling with polynomial functions , we focused on the first part of the modeling process: identifying the problem and creating and analyzing the model. Now, while modeling rational functions with real-world phenomena, we will focus on the second half of the modeling process: interpreting results and revising the model.
Interpreting results, drawing conclusions, and revising models
After a problem has been identified, the model is created. Then, we apply the model and analyze it for accuracy and effectiveness. We interpret the results that come from the use of the model and draw any relevant conclusions to the context.
Interpreting results includes the following:
Determining whether the answer makes sense in terms of the context
Identifying any extraneous solutions from the model that don't apply to the situation
Discussing the potential accuracy of the model depending on the limitations of the model or the assumptions we made when creating the model
At some point during analyzing or interpreting the model, we may realize the model needs to be revised. There are several different reasons a model might need to be modified. Here are some examples:
There might be an error in calculations, assumptions, or use of units.
We may have new or more relevant information to work with, requiring adjustments.
Sometimes our model needs fixing because we didn't consider all the consequences of making certain choices. For example, a problem involving a range of rates requires some choices to be made about what rate to use in that range. After analyzing the model, we may decide to choose a different rate analysis, not because of new information or an error, but because we realize a different choice would provide better information or be more relevant to the problem situation.
In other cases, our model may be too limited and need to be revised to account for broader considerations.
Examples
Example 1
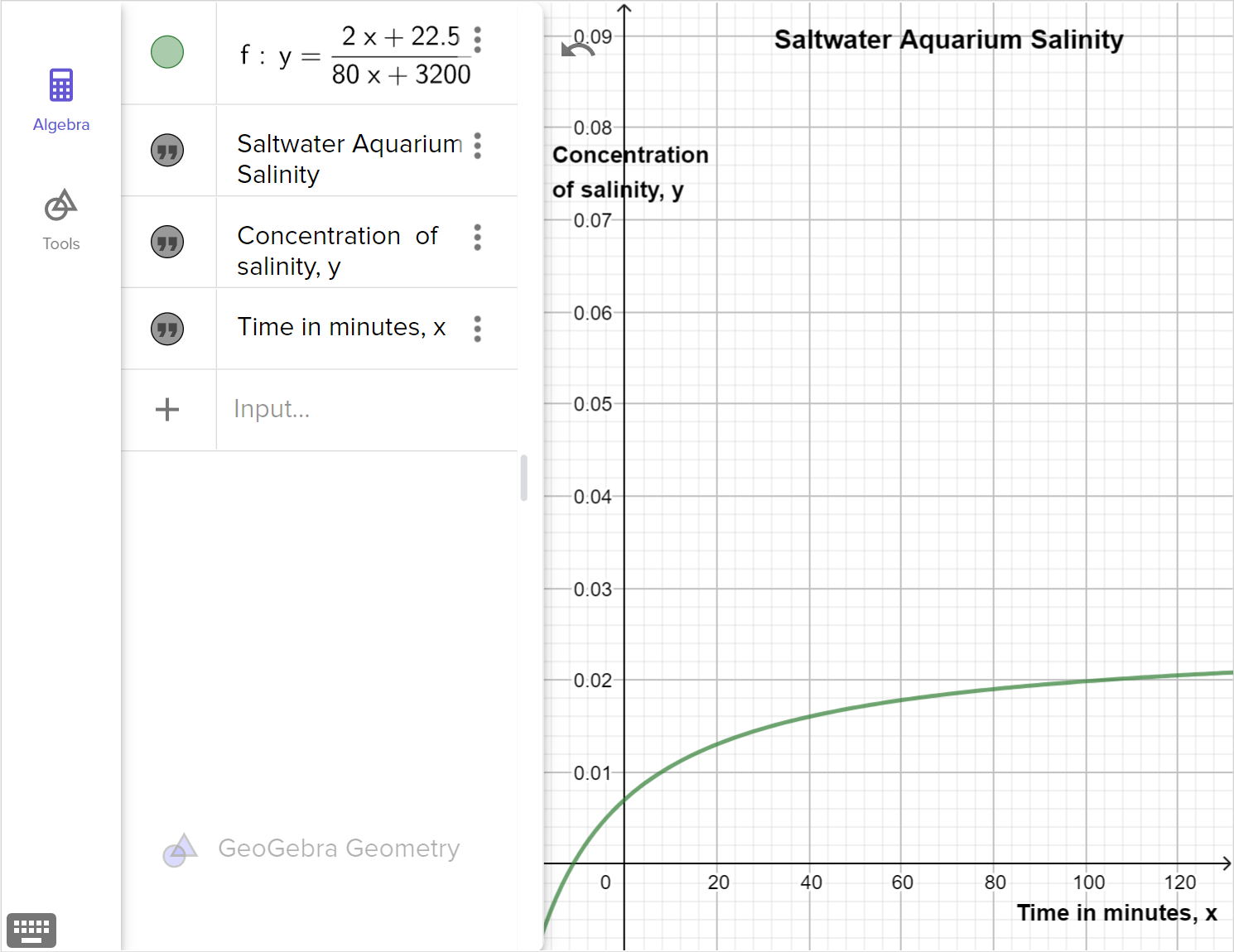
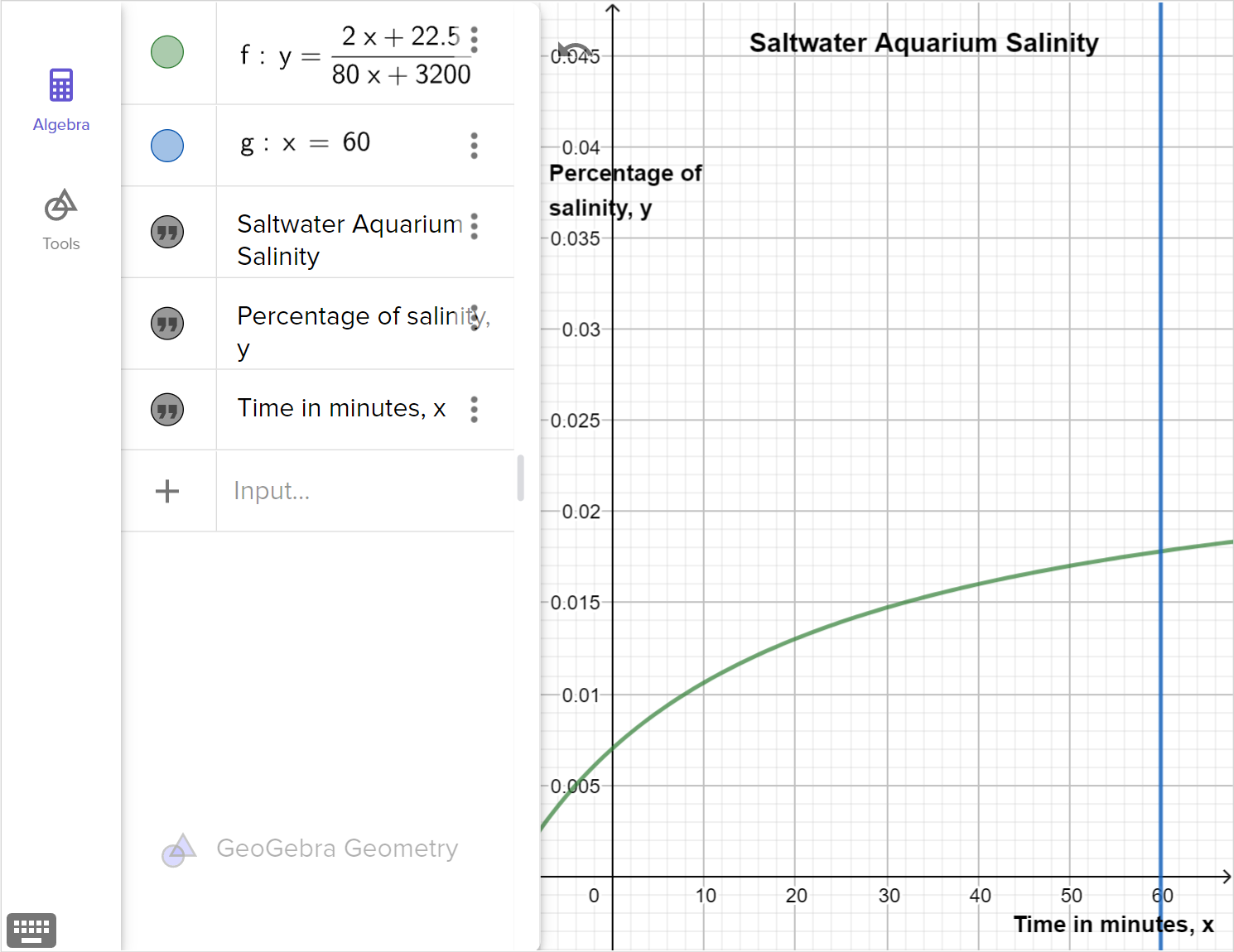
200 \text{ gallons} of water are mixed in a 500-gallon aquarium with 22.5 cups of reef salt. A hose, when turned on, will add water at a rate of 5 \text{ gal/min} while salt is poured in at a rate of 120 \text{ c/hr}.
Note that the safety of salinity for a saltwater aquarium is between 1 \% and 3 \%.
Reyita proposed the following function to model the concentration of the salt per gallon over time in the aquarium, where x represents the time in minutes and f \left(x \right) represents the cups of salt per gallon:f \left( x \right) = \dfrac{2x + 22.5}{5x+200}
The following graph models the function that shows the concentration of the saltwater:
The following table models the water and salt content of the aquarium for the first 15 minutes in intervals of 5:
| Time (Minutes) | Water (Gallons) | Salt (Cups) |
|---|---|---|
| 0 | 200 | 22.5 |
| 5 | 225 | 32.5 |
| 10 | 250 | 42.5 |
| 15 | 275 | 52.5 |
Examine the equation, graph and table that model this context. Are they all accurate models of the situation? If so, explain how the model matches the context. If not, identify any problems with the model, and revise the model to address the problems.
What are the limitations of our model in terms of the context?
Determine the conclusions that can be drawn from our model. State assumptions that were made, if any.
Example 2
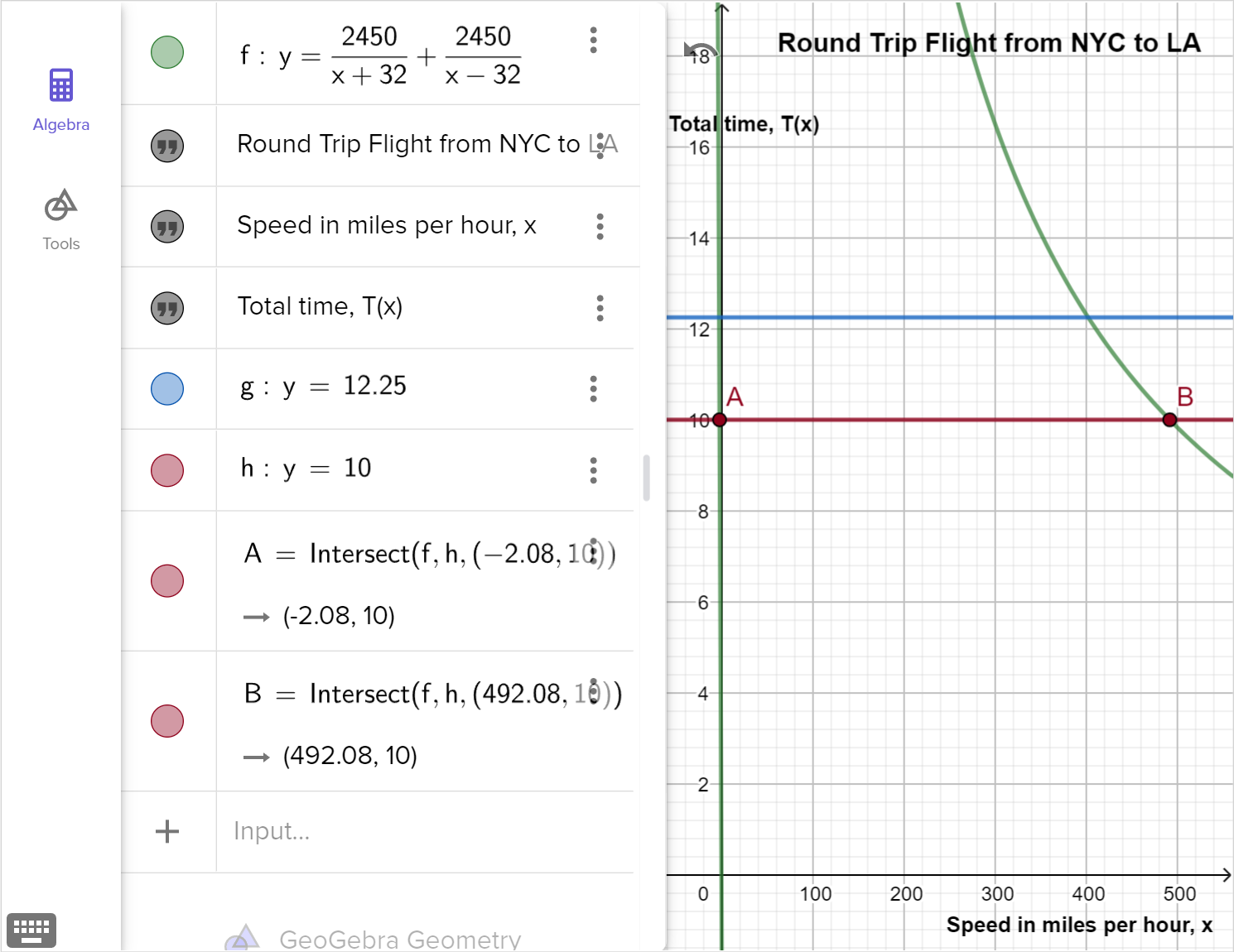
On a given day flying from New York City, NY to Los Angeles, CA, the tailwind from New York City to Los Angeles will increase the plane's speed. The return flight from Los Angeles against the wind will decrease the plane's speed. Suppose that the speed of the wind is 32 \text{ mi/hr}. The round trip flight takes anywhere from 10 hours to 12 hours and 15 minutes.
Maelys looks up the distance to fly from NYC to LA, which is approximately 2\,450 miles. Then she creates a table, equation, and graph to model the context assuming the round trip flight is scheduled to be a total of 12 hours and 15 minutes. Maelys identifies the unknown speed of the plane in miles per hour as x, and uses this in the equation:\text{Time to LA} + \text{Time to NYC} = \text{Total Time}
A table that organizes the given data follows:
| Distance | Rate | Time | |
|---|---|---|---|
| Tailwind | 2\,450 \text{ miles} | x + 32 \text{ mi/hr} | \dfrac{2\,450}{x+32} |
| Headwind | 2\,450 \text{ miles} | x- 32 \text{ mi/hr} | \dfrac{2\,450}{x-32} |
The equation that Maelys writes to model the context and can be used to find the speed of the plane is: \dfrac{2\,450}{x+32} + \dfrac{2\,450}{x-32} = 12.25
Finally, Maelys uses technology to graph the function for the speed of the plane when the trip takes 12 hours and 15 minutes:
Examine the equation, graph and table that model this context. Are they all accurate models of the situation? If so, explain how the model matches the context. If not, identify any problems with the model, and revise the model to address the problems.
Determine the average speed of the plane if the total trip time is 12 hours and 15 minutes, and interpret the results.
Revise the model to be useful for comparing any trip times within the given range. Describe any limitations or assumptions in the model.
The ability to interpret the results of a model and make evidence-based decisions is an important part of the modeling process. We can always utilize new information, or re-examine existing information, to make improvements to a model, influencing further decisions.