3.6 Sinusoidal function transformations
Introduction
Learning objective
- 3.6.A Identify the amplitude, vertical shift, period, and phase shift of a sinusoidal function.
Transformations of sine and cosine functions
Exploration
Explore the applet by dragging the sliders
How does changing each slider affect the graph of sine or cosine?
Is it possible to move the graph of cosine exactly on top of the graph of sine?
The graphs of sine and cosine experience transformations that change the key features of the functions and can be considered sinusoidal functions.
Since the graph of cosine can be transformed to be identical to the graph of sine, we also consider it to be sinusoidal.
The general form of a sinusoidal function changes the amplitude, frequency, and midline of the sine and cosine graphs.
Examples
Example 1
Sketch a graph and state the amplitude for each of the following functions.
f \left( x \right) = 5 \sin x
The graph of y= \cos x is reflected across the x-axis, then compressed in the vertical direction so that its minimum value is -\dfrac{3}{4}.
Example 2
Consider the function g \left( x \right) shown on the coordinate plane:
Compare the period, midline, amplitude, and domain and range of g \left( x \right) to the key features of the parent function f \left(x \right) = \sin x.
Write the equation of g \left( x \right).
Example 3
Consider the function f \left(x \right) = \sin x and g \left( x \right) = \sin \left( x - \dfrac{\pi}{2} \right).
Complete the table of values for both functions:
| x | 0 | \dfrac{\pi}{2} | \pi | \dfrac{3 \pi}{2} | 2 \pi |
|---|---|---|---|---|---|
| f\left( x \right) | |||||
| g\left( x \right) |
Graph f \left(x \right) and g \left(x \right) on the same coordinate plane.
Describe the transformation from f \left(x \right) to g \left(x \right).
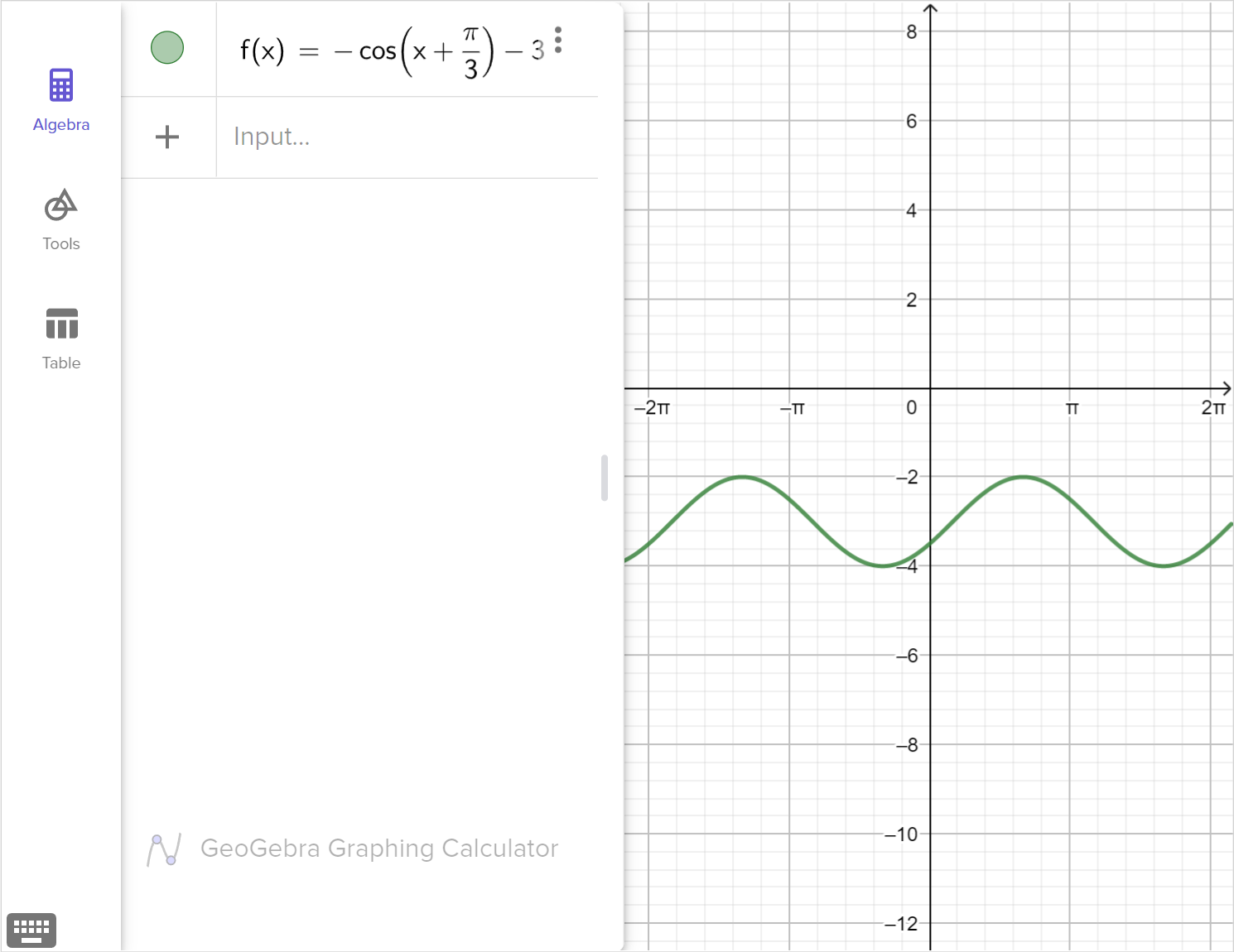
Example 4
The graph of the function f\left(x\right)=\cos x is transformed as follows:
The graph is reflected across the x-axis
The graph is horizontally translated to the left by \dfrac{\pi}{3}
The graph is vertically translated downwards by 3 units
Graph the transformed function described.
Determine the equation of the transformed function in the form g \left(x \right) = a\cos \left[b \left( x - c \right)\right] + d, where c is the least positive value in radians.
State the midline, amplitude, period, and domain and range of the function.
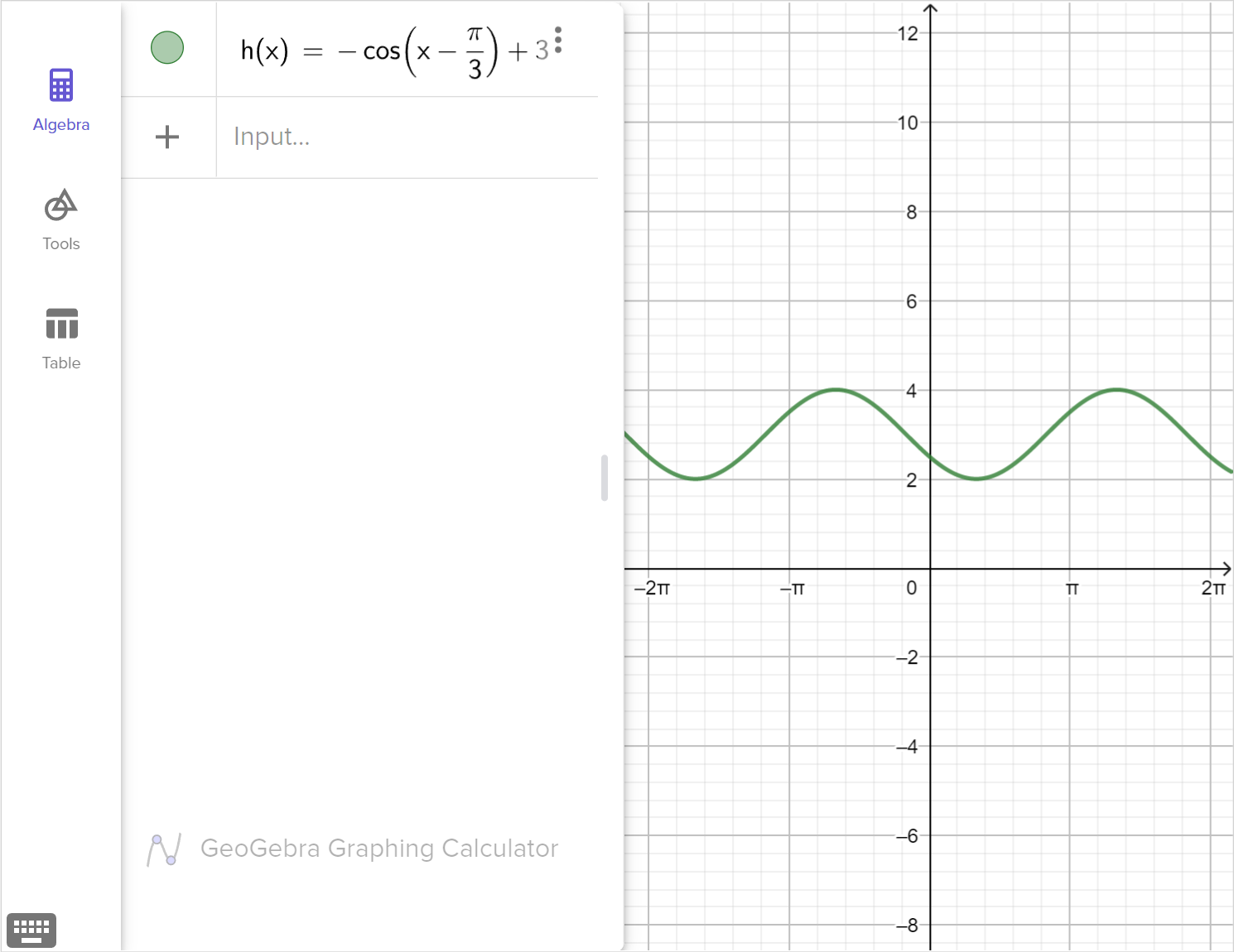
Explain how the graph and function would be different if we performed the translations before the reflection.
Refer to the general form of the sinusoidal function to write or determine transformations to f \left( x \right) = \sin x: