11.02 Parallel and perpendicular lines
Introduction
We will continue building our understanding of parallel and perpendicular lines by considering characterstics seen in their rates of change. We will use the slope formula from Math 1 lesson 3.05 Graphing linear functions to prove whether lines are parallel or perpendicular in the coordinate plane.
Ideas
Parallel lines
Exploration
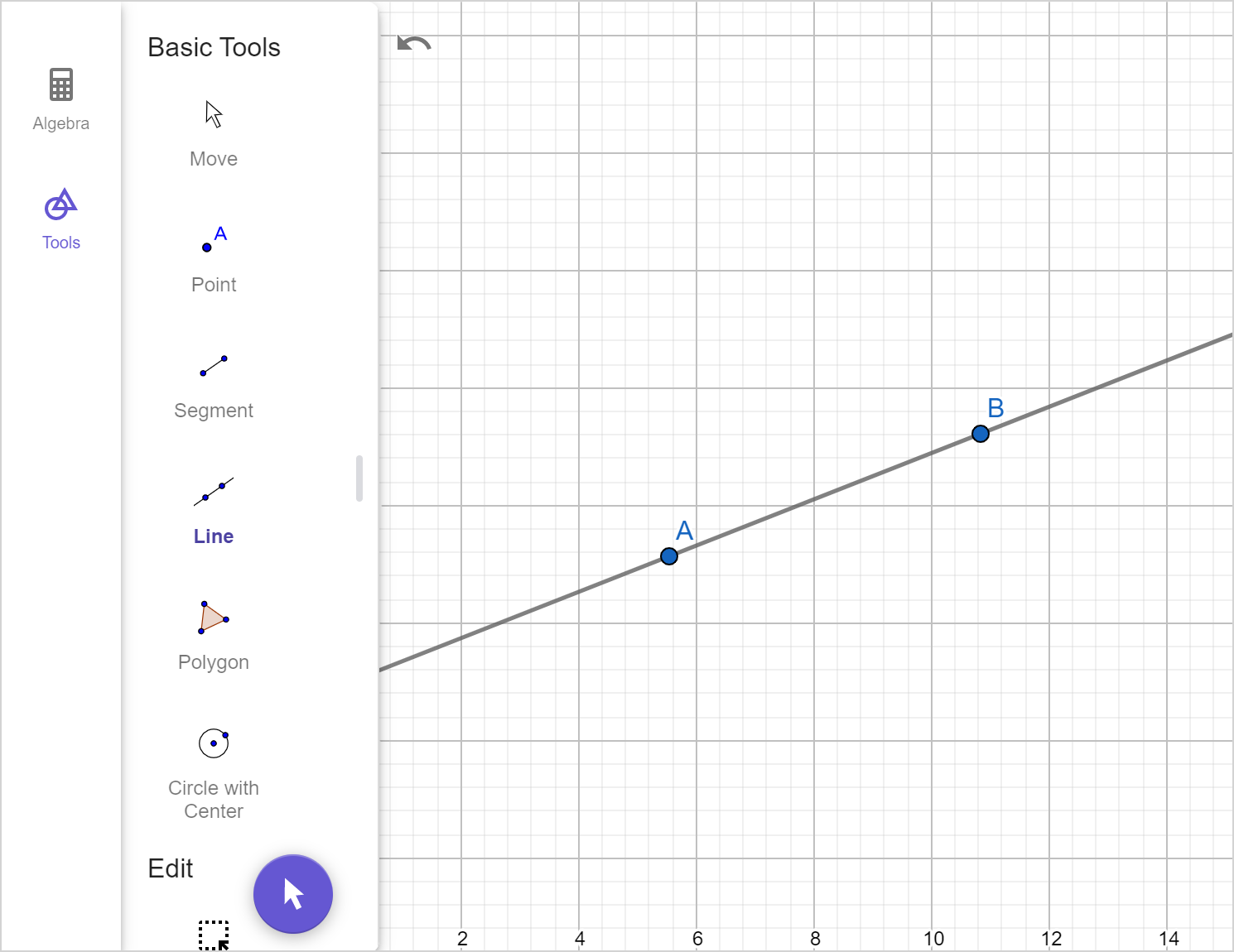
Move each of the blue points around. The points on the y-axis will move up and down, and the other point can move anywhere.
- What do you notice about the slopes of the two parallel lines?
- Do you think this is true for all non-vertical lines?
- How could we prove two lines are parallel?
Parallel lines will always have the same slope. This means they will never intersect. Any two vertical lines are parallel.
We can use this theorem to prove lines are parallel and to find the equations of parallel lines.
Examples
Example 1
Prove that the lines are parallel.
Example 2
The line AB passes through the points \left(-2,9\right) and \left(3,-21\right).
Write the equation of the line.
Find the equation of the line that passes through \left(1,5\right) and is parallel to the line AB.
Example 3
Prove that two non-vertical lines are parallel if their slopes are the same.
If two lines are parallel, they have the same slope.
If two lines have the same slope, they are parallel.
Perpendicular lines
Exploration
Drag the blue points around. Keep the point on the red line in between the other two points for easier usability.
- What do you notice about the slopes of the two perpendicular lines?
- Do you think this is true for all non-vertical perpendicular lines?
- How could we prove two lines are perpendicular?
Perpendicular lines have slopes with opposite signs and they are reciprocals of one another. A vertical and horizontal line are perpendicular.
We may also call the slopes of perpendicular lines opposite reciprocals which refers to them being reciprocals with opposite signs. We use this theorem to prove lines are perpendicular and to find the equations of perpendicular lines.
Examples
Example 4
Consider the lines on the given coordinate plane.
Identify all pairs of parallel lines.
Identify all pairs of perpendicular lines.
Example 5
Consider the line 4x-3y=-6.
Find the equation of the line that is perpendicular to the given line and has the same y-intercept.
Write the equation in standard form.
Example 6
A mirror is placed along the x-axis. A laser beam is projected along the line y=-x+4 which reflects off the mirror.
A normal is a line which is perpendicular to the surface of the mirror at the point of reflection. Find the equation of the normal.
The angles that the laser and its reflection make with the normal will be congruent. If the angle between the laser beam and the normal is 45 \degree, find the equation of the path of the reflection.
Example 7
Prove that two non-vertical lines are perpendicular if the product of their slopes is -1.
The slopes of perpendicular lines are reciprocals with opposite signs. When multiplied together, they have a product of -1.
Constructing parallel lines
Exploration
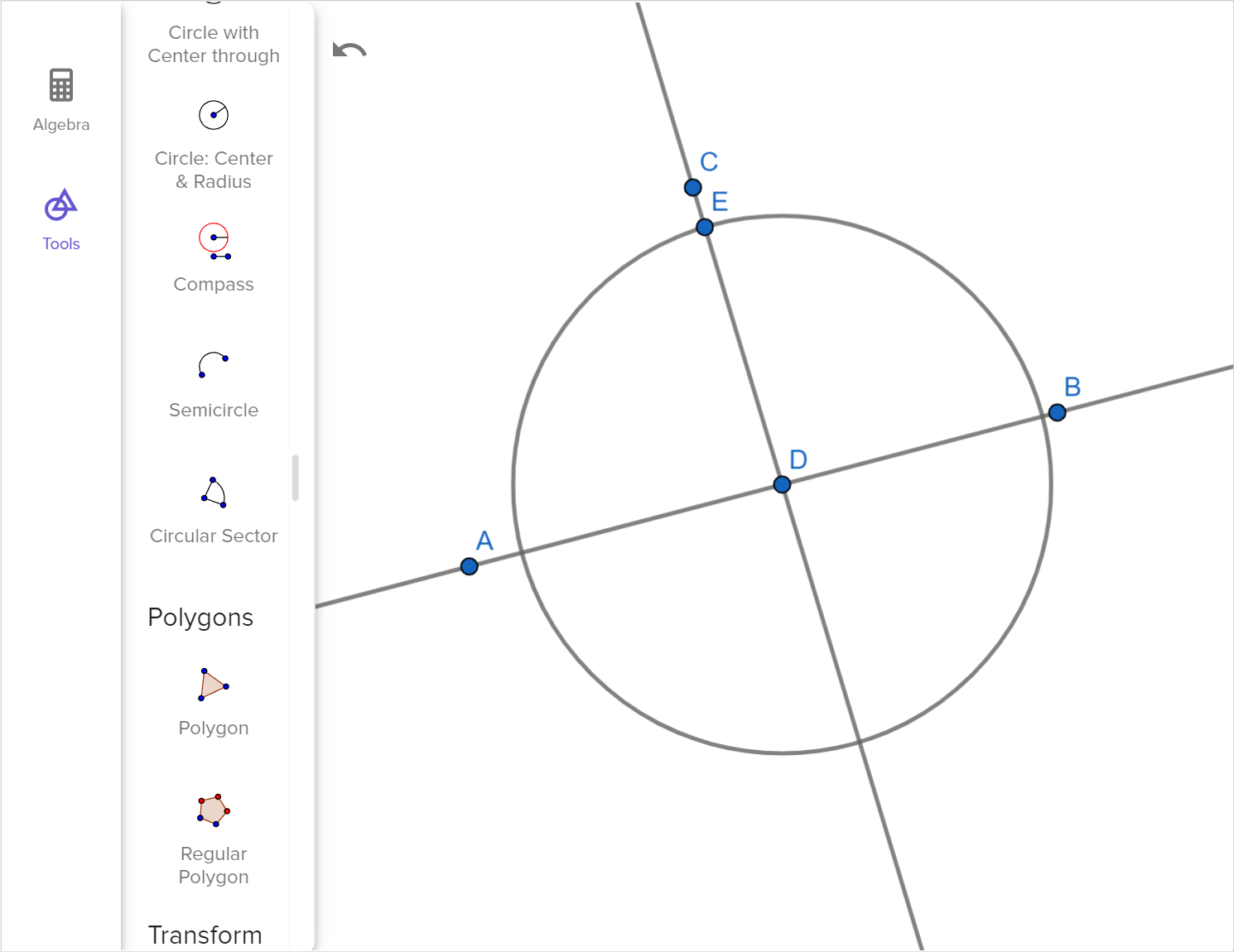
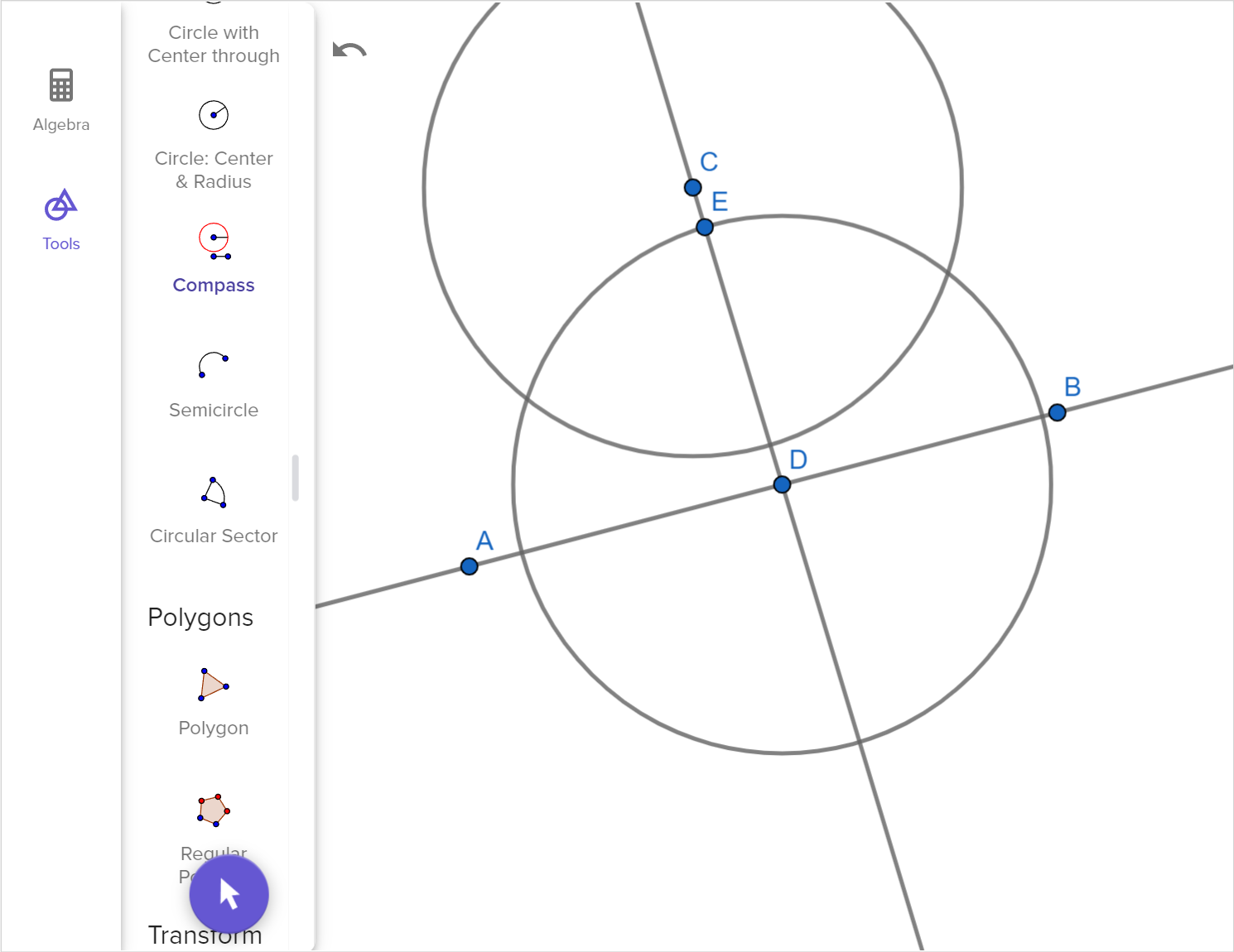
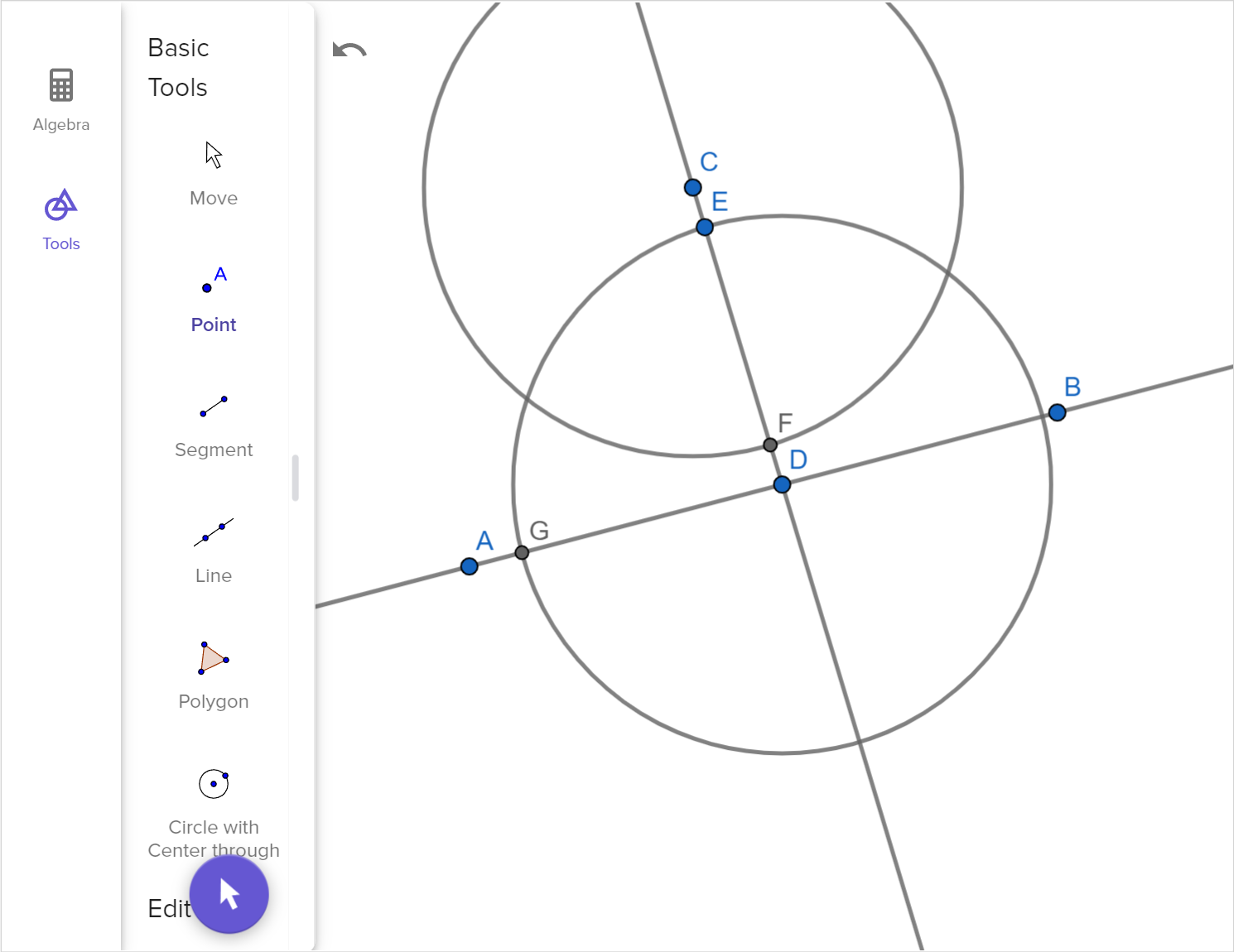
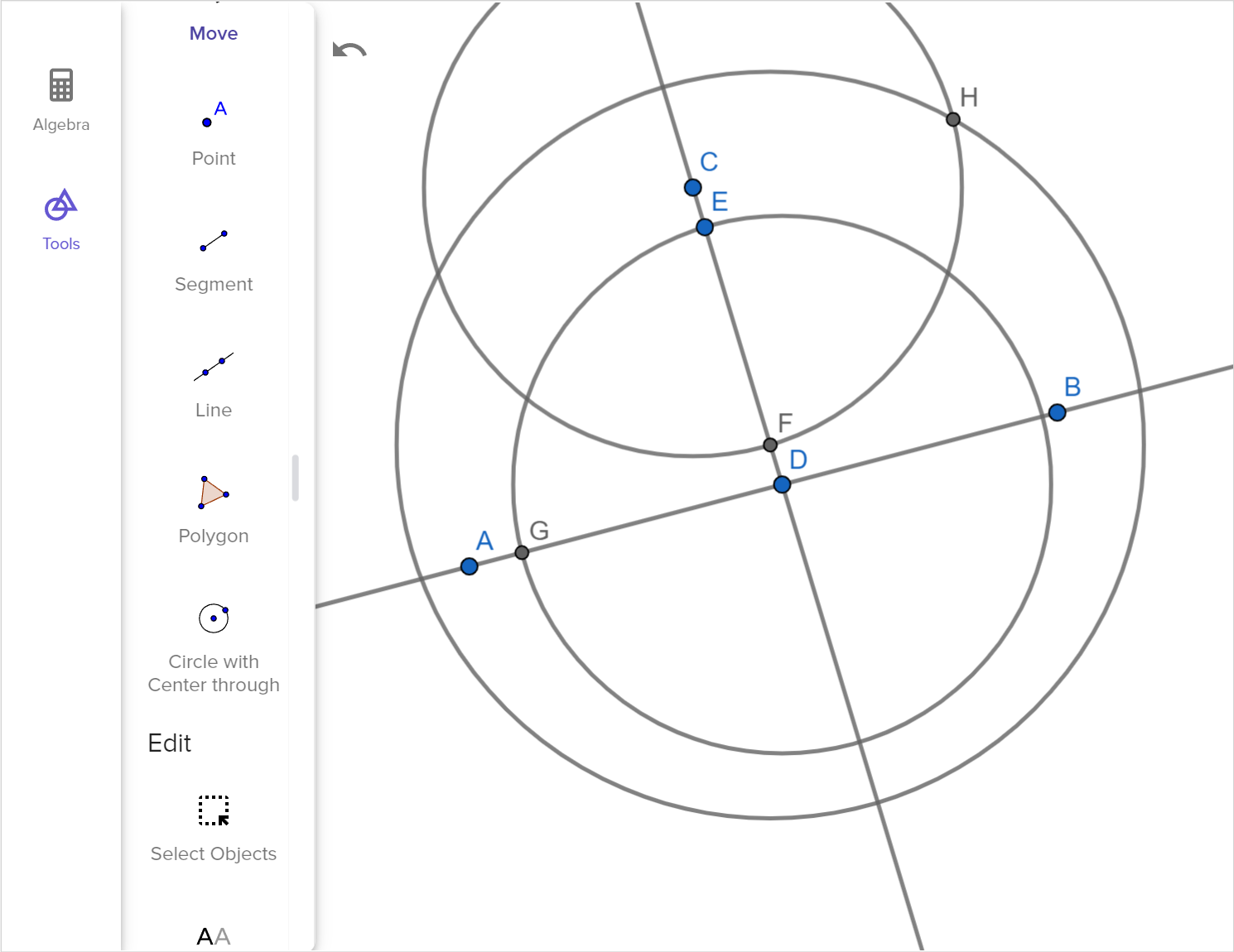
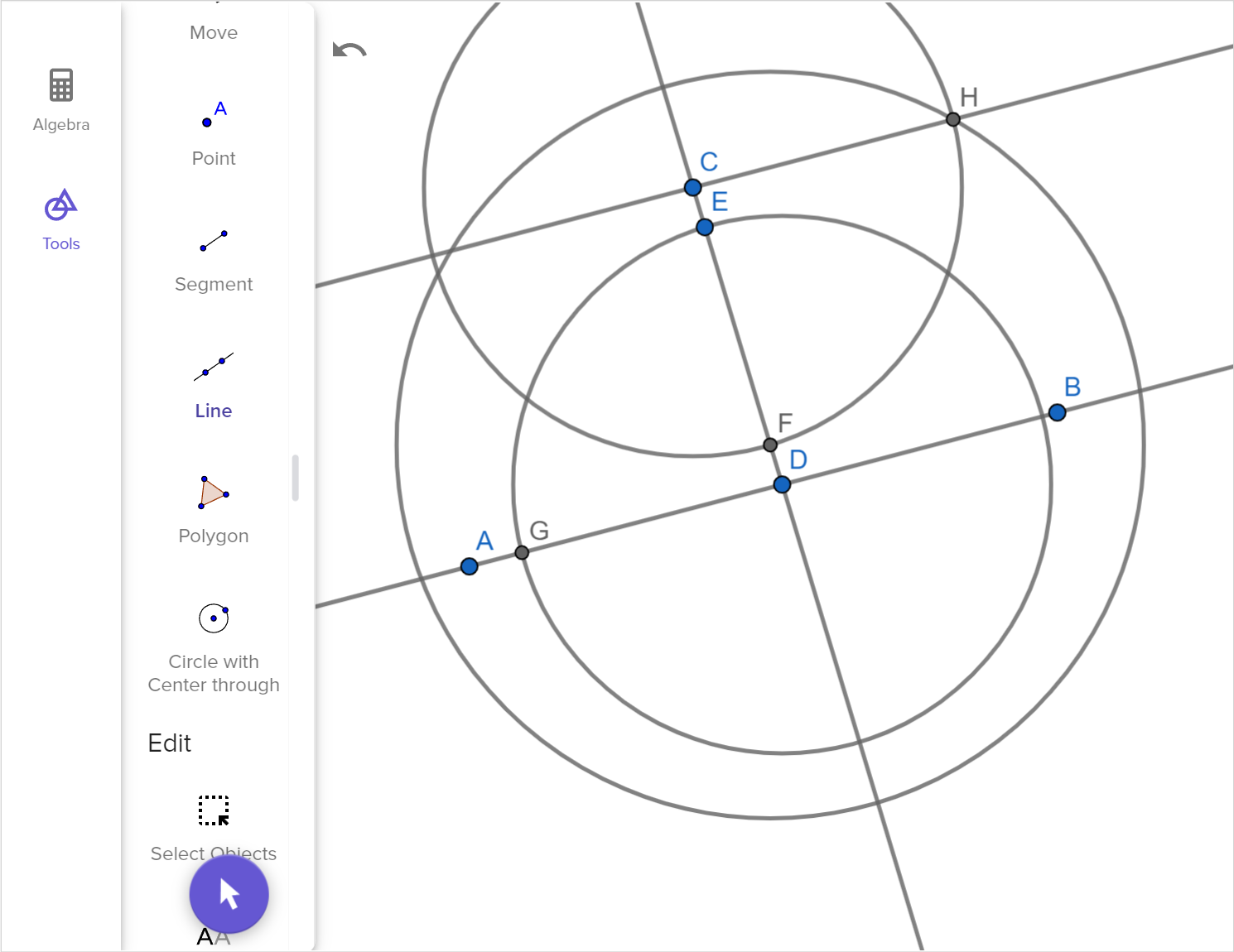
Click through the slides of the parallel line construction.
- Describe what is happening in each step.
We can construct a set of parallel lines using dynamic geometry software. Another way to construct parallel lines using a compass and straightedge as follows:
1. Choose a point A through which to construct a line parallel to \overleftrightarrow{BC}.
2. Set the compass width to the distance AC.
3. Construct an arc centered at B with the radius AC.
4. Set the compass width to the distance AB.
5. Construct an arc centered at C with the radius AB.
6. Construct a line through A and the intersection of the two arcs. This line is parallel to \overleftrightarrow{BC}.
Notice, here we did not draw the full circles as was done with the dynamic geometry software. We could have drawn the full circles but it is only necessary to draw enough of the arcs of each circle to make the necessary points of intersection. Drawing a construction this way prevents creating any unnecessary points of intersection that may cause confusion.
Examples
Example 8
Use constructions to construct two parallel lines.
We can use various methods to construct parallel lines including technology and a compass and straightedge.
Proofs and constructions of perpendicular lines
Exploration
Drag points A, B, and P to change the lengths.
- What relationships in the diagram are always true? Can you explain why?
A point, line, or ray that is perpendicular to a line segment at its midpoint is a perpendicular bisector.
To construct a perpendicular line, we can use the following method:
Choose two points on a given line.
Construct an arc centered at one of the points.
Construct an arc centered at the other point, such that this arc intersects the arc constructed in Step 2 at two distinct points.
Plot points where the two arcs intersect. Here we have used A and A'.
Construct the line \overleftrightarrow{AA'}. It is perpendicular to the line constructed in Step 1.
If we want the perpendicular line to pass through a particular point, we can adjust the radii of the compass so that both arcs pass through that point.
Examples
Example 9
Recall that the Pythagorean theorem states that given a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of its legs lengths.
Prove the perpendicular bisector theorem.
Example 10
Construct a proof of the following:
Given m \angle1 = m \angle 2
Prove: l \perp m
Example 11
Ludek is creating a shirt design on his computer. He wants to include some perpendicular lines as part of the design, but the program he is using doesn't measure angles so he can't construct them directly using a right angle.
The program Ludek is using can construct lines and circles accurately through or centered at points. Describe how Ludek could construct the perpendicular lines for his design.
Example 12
Construct perpendicular bisector \overleftrightarrow{CD} through \overline{AB}.
We can use the relationships between angles to prove that lines are perpendicular. We can use various methods to construct perpendicular lines including technology and a compass and straightedge.