7.02 Fitting functions to data
Introduction
We sketched and interpreted lines of best fit in lesson 7.01 Scatter plots and lines of fit . We will learn how to calculate the line of best fit and the correlation coefficient using technology and then extend the concept to modeling exponential relationships.
Fitting functions to data
Exploration
Use the linear and exponential models to fit the data on the graph.
- Which function fits the data better? How do you know?
Sometimes we need to consider fitting something other than a line of best fit or regression line, which both refer to a linear regression model, to model data. A fitted function could include another type of function, such as an exponential function.
We already learned about the correlation coefficient, r, a statistic that describes both the strength and direction of a linear association. But, we also need a measure that determines how well our fitted function can actually predict an outcome.
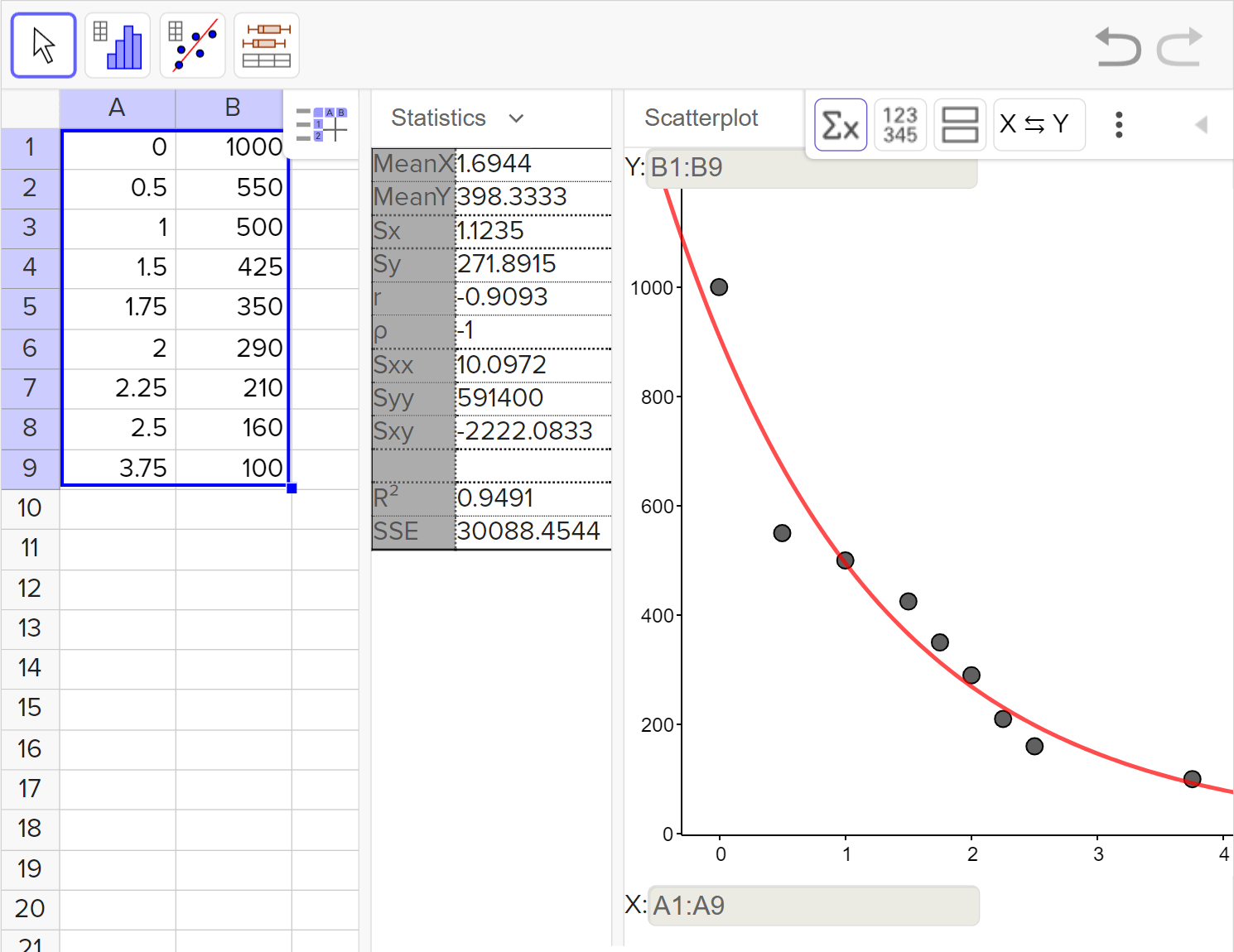
This value is known as the coefficient of determination, or the value R^2, and is a measure of the proportion of the variation in the dependent variable that is predicted by the independent variable. Since the coefficient of determination represents a proportion it will only ever return a value between 0 and 1.
In the case where the fitted function is a linear model with one independent variable, R^2 is equal to our correlation coefficient squared, r^2. This only holds true for linear models with one independent variable and is not the case when the fitted function is from any other function family, e.g. exponential, quadratic, etc.
Bivariate data can be modeled with a fitted function also called a regression model. Depending on the goodness of fit, measured with the coefficient of determination (R^2), a regression function may pass exactly through all of the points, some of the points, or none of the points.
\text{ Exponential regression } R^2=0.763
R^2 for the exponential regression shown means that 76.3\% of the variation in the dependent variable is explained by the variation in the independent variable. The closer R^2 is to 1, the more that the variation in the dependent variable is explained by the variation in the independent variable.
Examples
Example 1
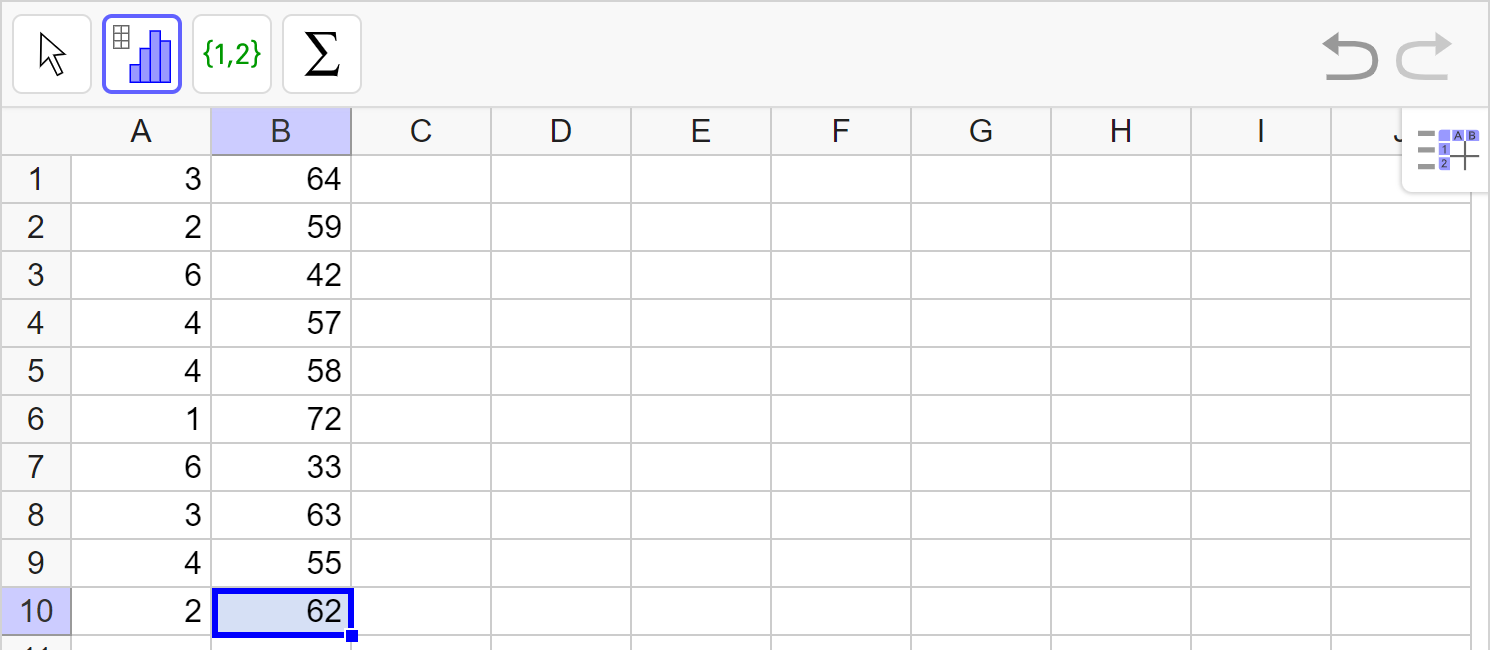
A teacher recorded the number of days since a student last studied for an exam and their score out of a possible 80 points on the exam.
| Number days since studying | 3 | 2 | 6 | 4 | 4 | 1 | 6 | 3 | 4 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Exam score | 64 | 59 | 42 | 57 | 58 | 72 | 33 | 63 | 55 | 62 |
Describe the association between the number of days since student and the exam score.
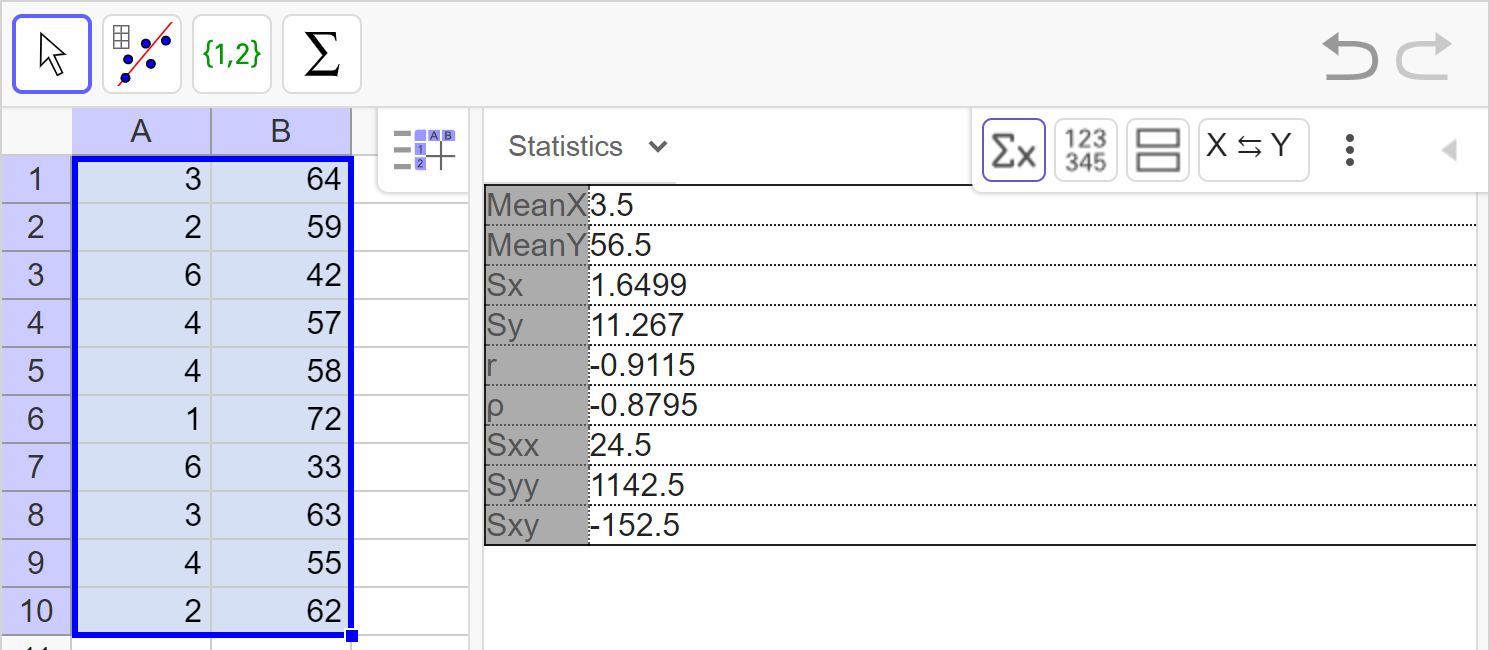
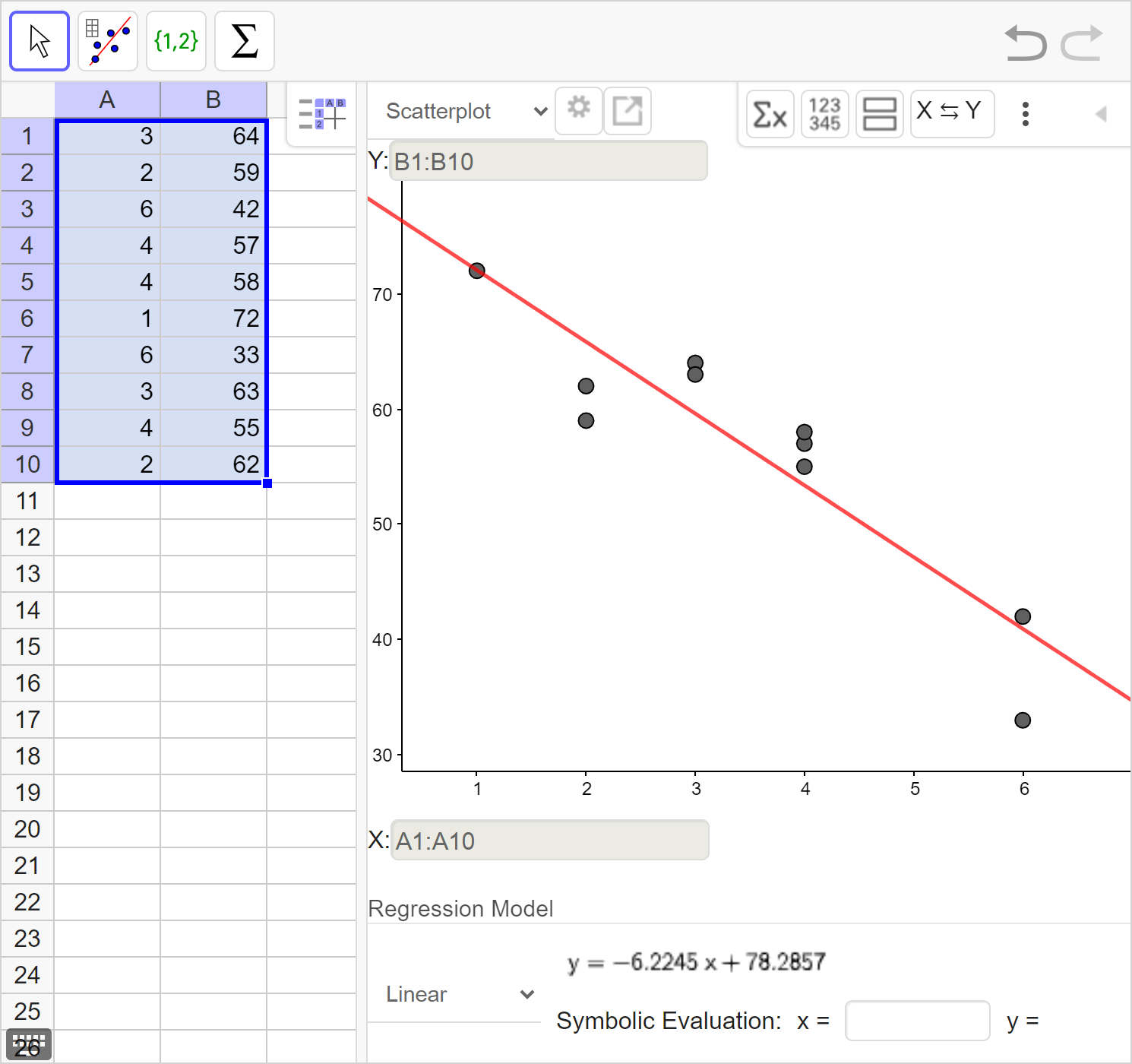
Calculate the line of best fit and correlation coefficient. Interpret the correlation coefficient.
Interpret the meaning of the slope and y-intercept of the line of best fit in context of the data.
Example 2
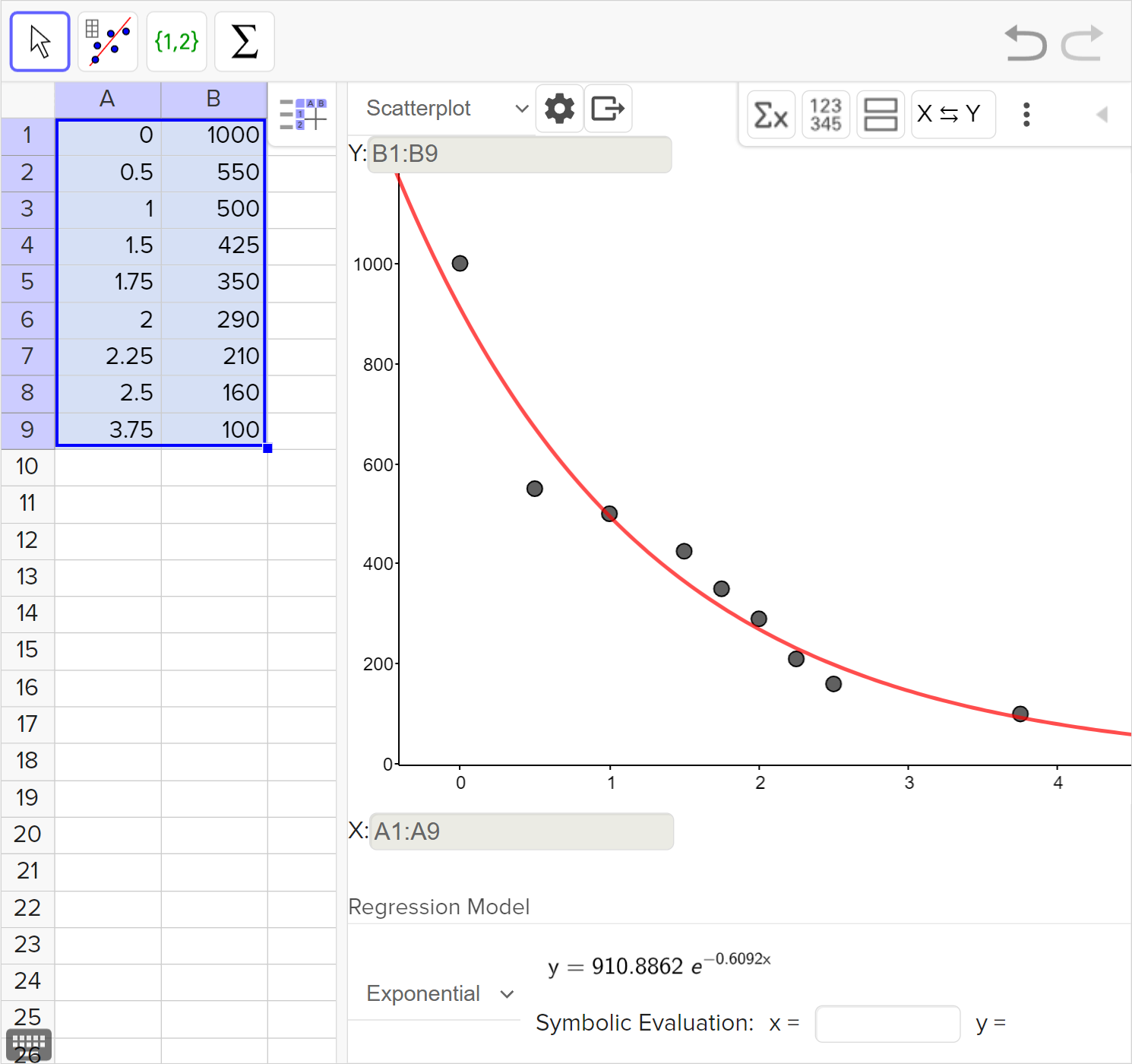
The population P of fish in a small lake over t years is shown in the table below:
| Years (t) | Fish Population (P) |
|---|---|
| 0 | 1000 |
| 0.5 | 550 |
| 1 | 500 |
| 1.5 | 425 |
| 1.75 | 350 |
| 2 | 290 |
| 2.25 | 210 |
| 2.5 | 160 |
| 3.75 | 100 |
Determine whether a linear or exponential model best fits the relationship between the years, t, and the population of fish P.
Calculate the regression model for the data and use it to predict the population of fish in the lake after 5 years.
Interpret the coefficient of determination for the regression model.
Linear and exponential data can be fitted to a regression model. We can analyze the closeness of the fit using the coefficient of determination.