It is now time to put the tools learned through the analysis of time series data to use through a statistical investigation.
The statistical investigation process
The following steps form a rigorous and complete statistical investigation process:
- Identify a problem
- Pose a statistical question
- Collect or obtain data
- Analyse data
- Interpret and communicate results
The problem
At the beginning of this unit of work was some real world data - the petrol price cycle.
Consider the following problem: Understanding the fuel price cycle for Perth.
The statistical question
When is the cheapest time to buy petrol in Perth and what price can be predicted for unleaded petrol on the cheapest day next week?
This analysis will be conducted in late February, early March, and "next week" is from Monday 29th February to Sunday March 6th 2016.
Collecting the data
To collect the data, head to Google and see what can be found for average price movements of unleaded petrol in Perth.
The ACCC is updated regularly with petrol prices in all major cities in Australia and is a great place to start.
Also, in Perth there's a website called FuelWatch so that residents can find where the cheapest places are in Perth on any given day. Furthermore, it is possible to download historical files of data.
The following data was downloaded from the Feburary 2016 file and petrol stations from all around Perth and country areas.
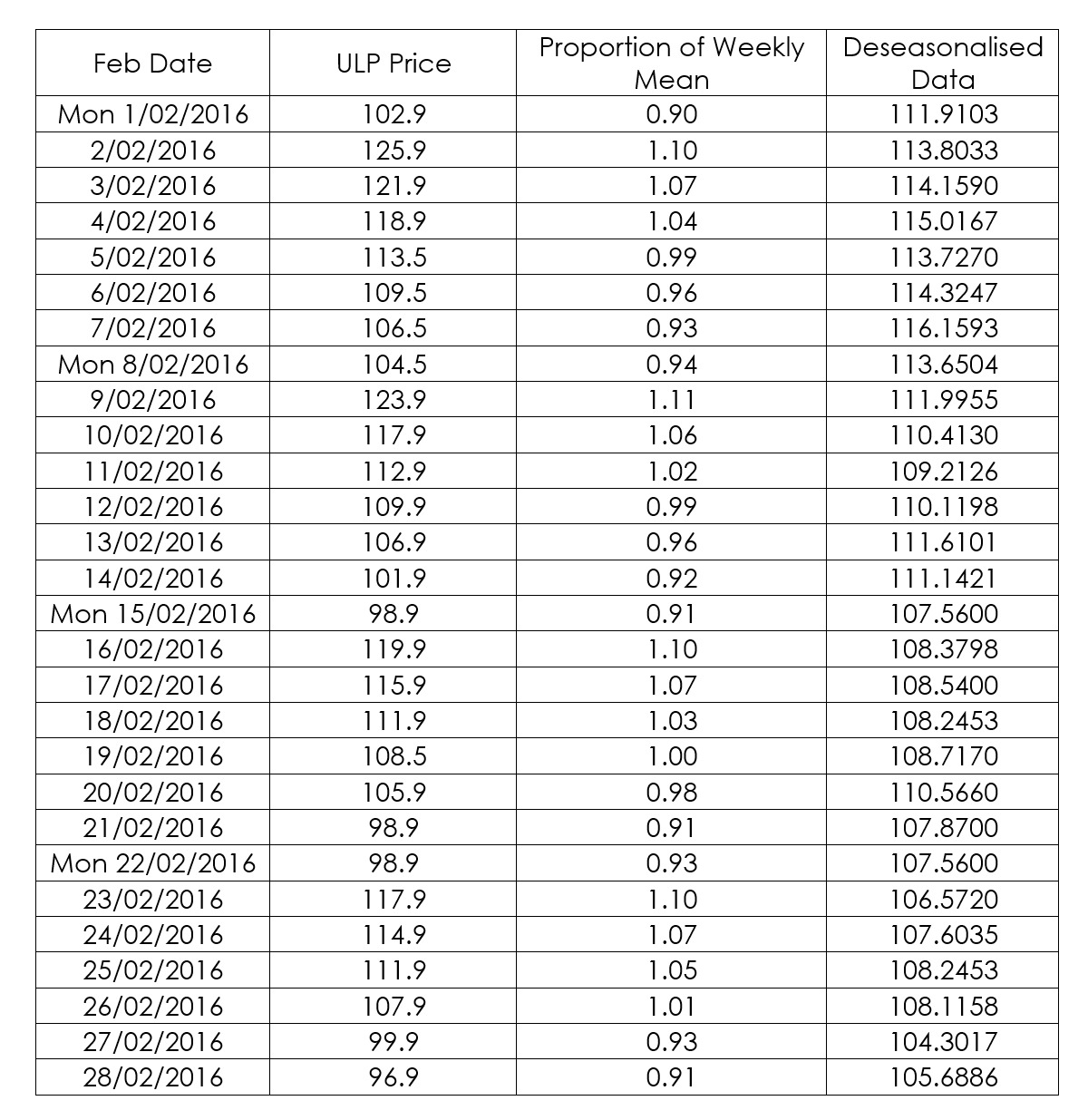
Here are the unleaded petrol prices for each day in February at one particular Caltex Petrol station in Balcatta.
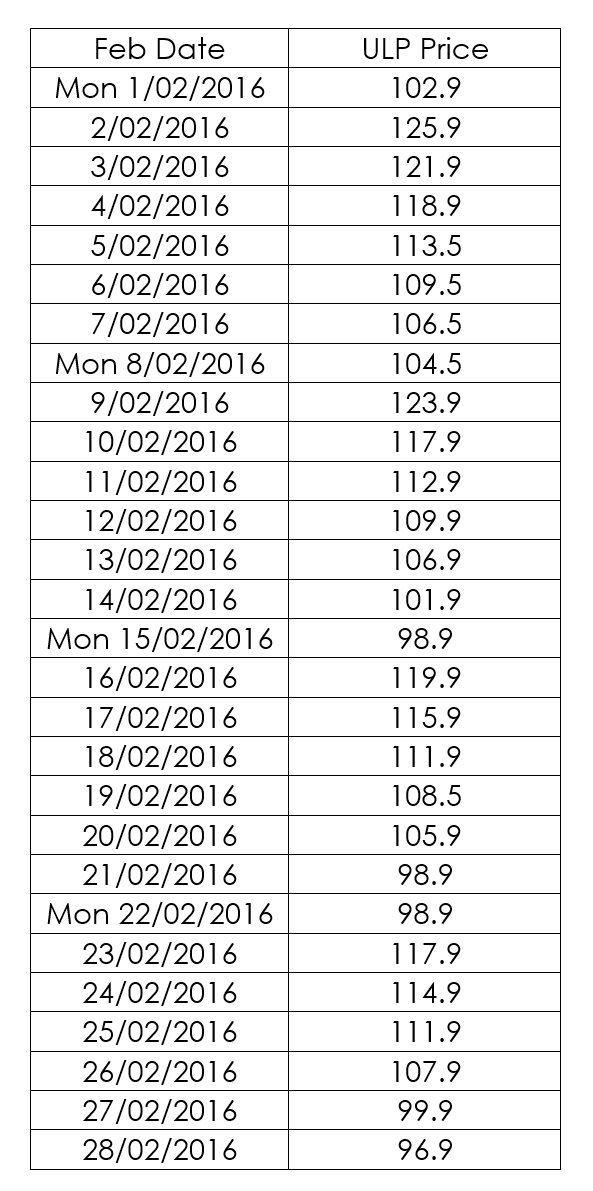
Using an Excel spreadsheet, a line graph can then be created in order to analyse the data.
Analysing the data
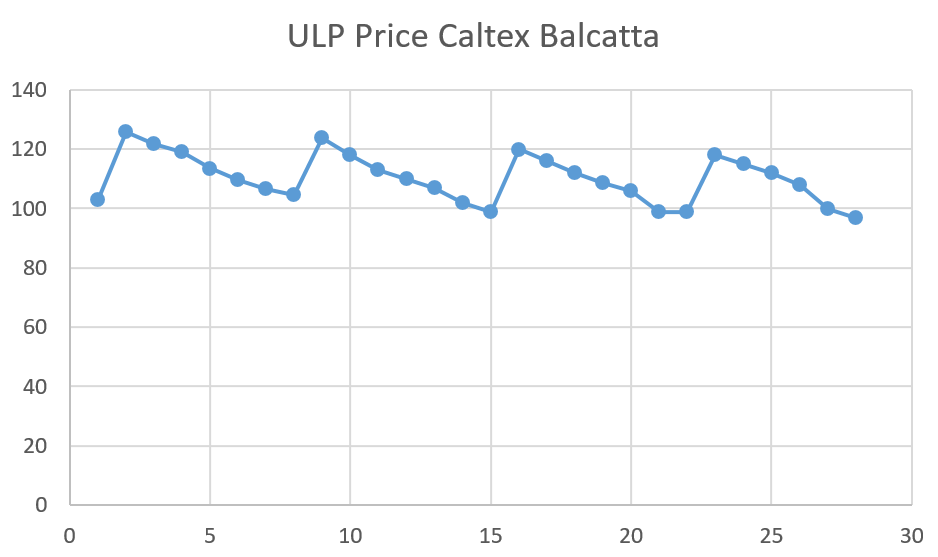
A clear seven day trend seems evident. It also appears that petrol prices are decreasing each week through a slight declining trend seen on the graph.
The first part of the statistical question is easily answered, fuel appears to be cheapest on a Monday. Therefore, people should aim to purchase their unleaded petrol on Monday 29th February.
To work out what it will cost on that day, by fitting a least squares line, the data first needs to be deseasonalised.
Firstly calculate the mean for each of the four weeks.
As an example, the weekly mean for week 1 would be calculated as follows:
\frac{102.9+125.9+121.9+118.9+113.5+109.5+106.5}{7}=114.1571428
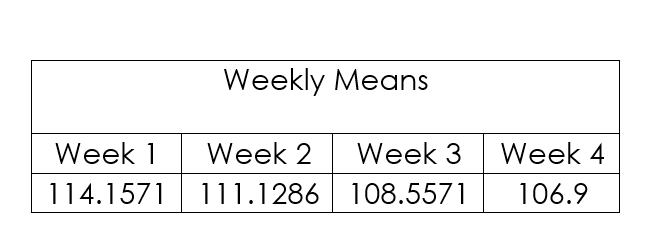
Then calculate each proportion of the weekly means followed by the seasonal indices.
Let's go through the steps for calculating the seasonal index for Monday. We will be using the ULP prices for each of the four Mondays as well as the weekly means.
Firstly we need to calculate the proportion of weekly mean by dividing the ULP Price for Monday by the relevant weekly mean:
| Monday | Proportion of weekly mean |
| Week 1 | \frac{102.9}{114.1571}=0.90139 |
| Week 2 | \frac{104.5}{111.1286}=0.940352 |
| Week 3 | \frac{98.9}{108.5571}=0.911041 |
| Week 4 | \frac{98.9}{106.9}=0.925164 |
Secondly, we find the average of the four proportion of weekly means which will give us the seasonal index for Monday.
| Seasonal Index for Monday |
| \frac{\frac{102.9}{114.1571}+\frac{104.5}{111.1286}+\frac{98.9}{108.5571}+\frac{98.9}{106.9}}{4}=0.91948679 |
The same procedure should be followed to calculate the seasonal indices for the remaining days.
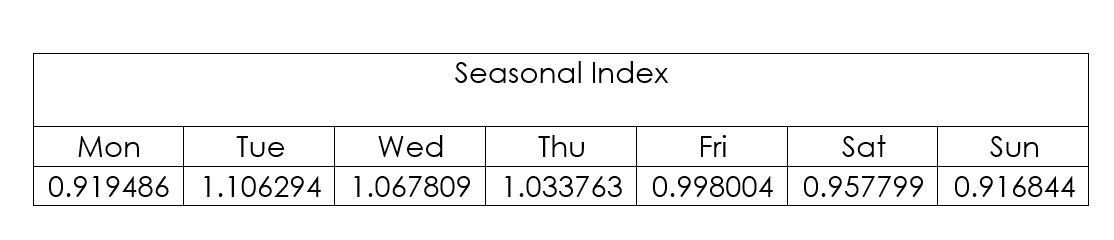
The data can then be deseasonalised. This is done by dividing the actual figure by the relevant seasonal index.
For example, the deseasonalised data for Monday 1/02/2016 is calculated by \frac{102.9}{0.919486}=111.9103.
A graph of the raw data along with the deseasonalised data shows the smoothing effect.
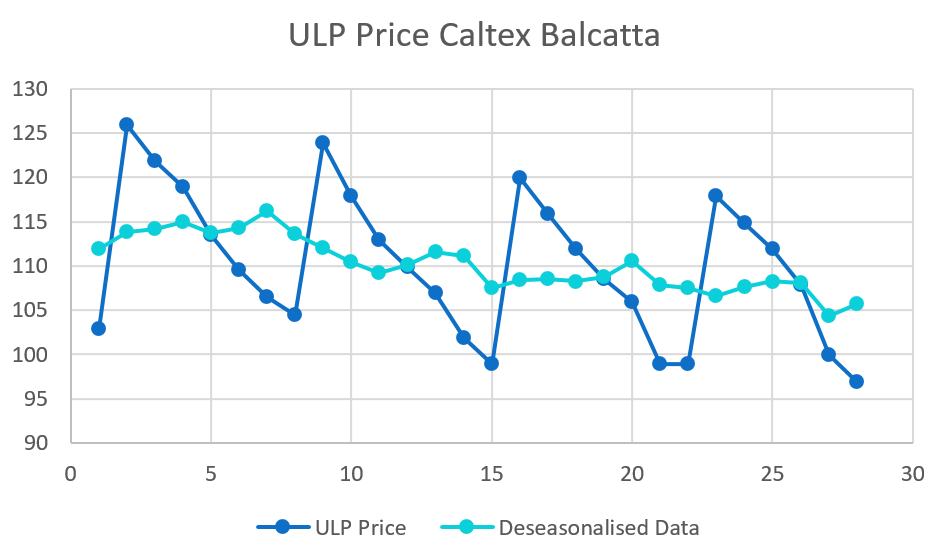
It is now possible to fit a least squares regression line to the deseasonalised data, where t = 1 is Monday 1st February.
Doing so obtains the following least squares regression line:
\hat{y}=-0.3278t+114.9397
This least squares line can now be used to predict what the petrol will cost on Monday 29th February 2016.
Note that t = 29 in this case.
\hat{y}=105.4324
Remember that this is a deseasonalised result and therefore seasonality needs to be added back into the prediction by multiplying it by the seasonal index.
105.4324\times0.9195=96.95 cents/litre
Interpreting and communicating the result
On Monday 29th February 2016, one can expect to pay 96.95 cents/litre for ULP at Caltex in Balcatta.
The prediction should be reliable as it is made within one cycle of the last available collected data.
Side note: In fact, on this day, the price was 93.9 cents/litre at the Balcatta Caltex, so even lower than anticipated by the historical records and the prediction.
To do
Find the most recent fuel price data for your own town or city and follow the process above to make a prediction as to the price on a particular day in the future.