3.04 Angle and perpendicular bisectors
Introduction
We first constructed angle bisectors in lesson 1.04 Angles and constructions and perpendicular bisectors in lesson 2.03 Perpendicular lines. We will construct angle bisectors and perpendicular bisectors in triangles in this lesson to solve problems and draw constructions.
Perpendicular bisectors
When a perpendicular bisector cuts a line segment at a right angle and into two congruent segments, we can use the perpendicular bisector theorem and the converse of the perpendicular bisector theorem to solve problems in angles and triangles.
Exploration
Draw three different triangles and construct the perpendicular bisectors of each side. Make sure each triangle is a different type: acute, obtuse, and right.
- What do you notice about the perpendicular bisectors of the first triangle?
- Does what you noticed with the first triangle hold true for the other two?
A point of concurrency is a point where three or more lines coincide. The perpendicular bisectors of a triangle intersect at the point of concurrency, called the circumcenter. The circumcenter is also the center of the circle that circumscribes the triangle.
Examples
Example 1
Find the value of x.
Example 2
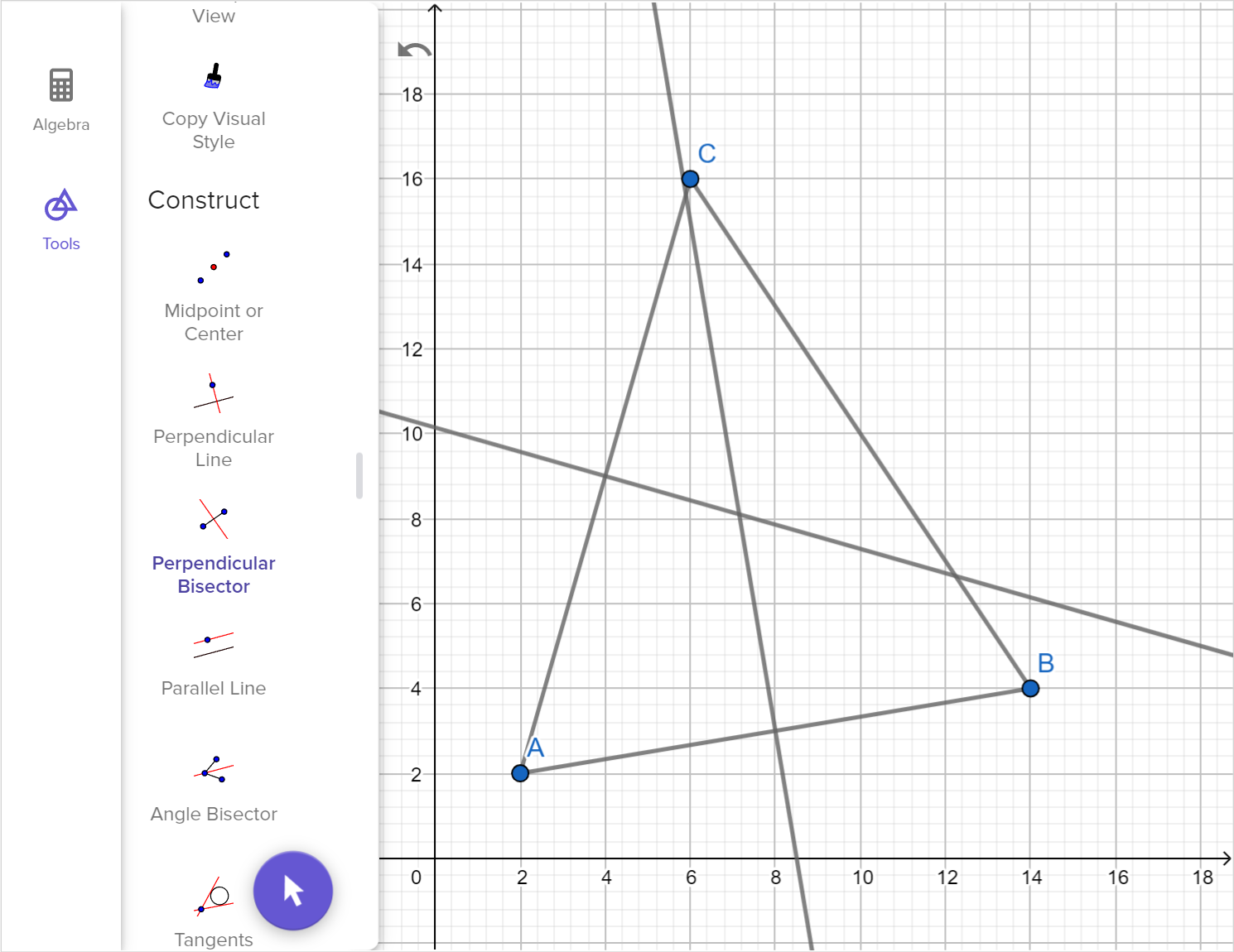
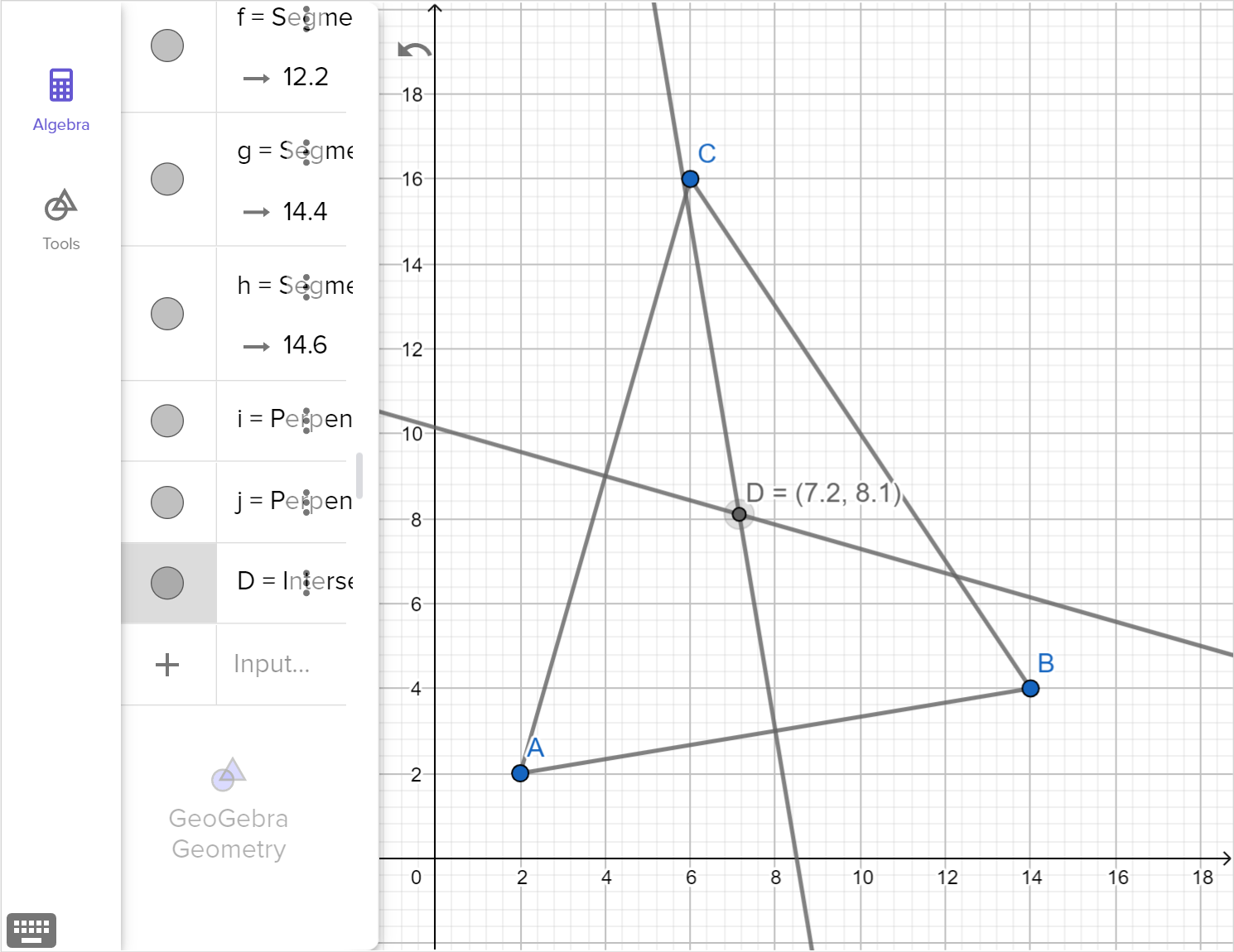
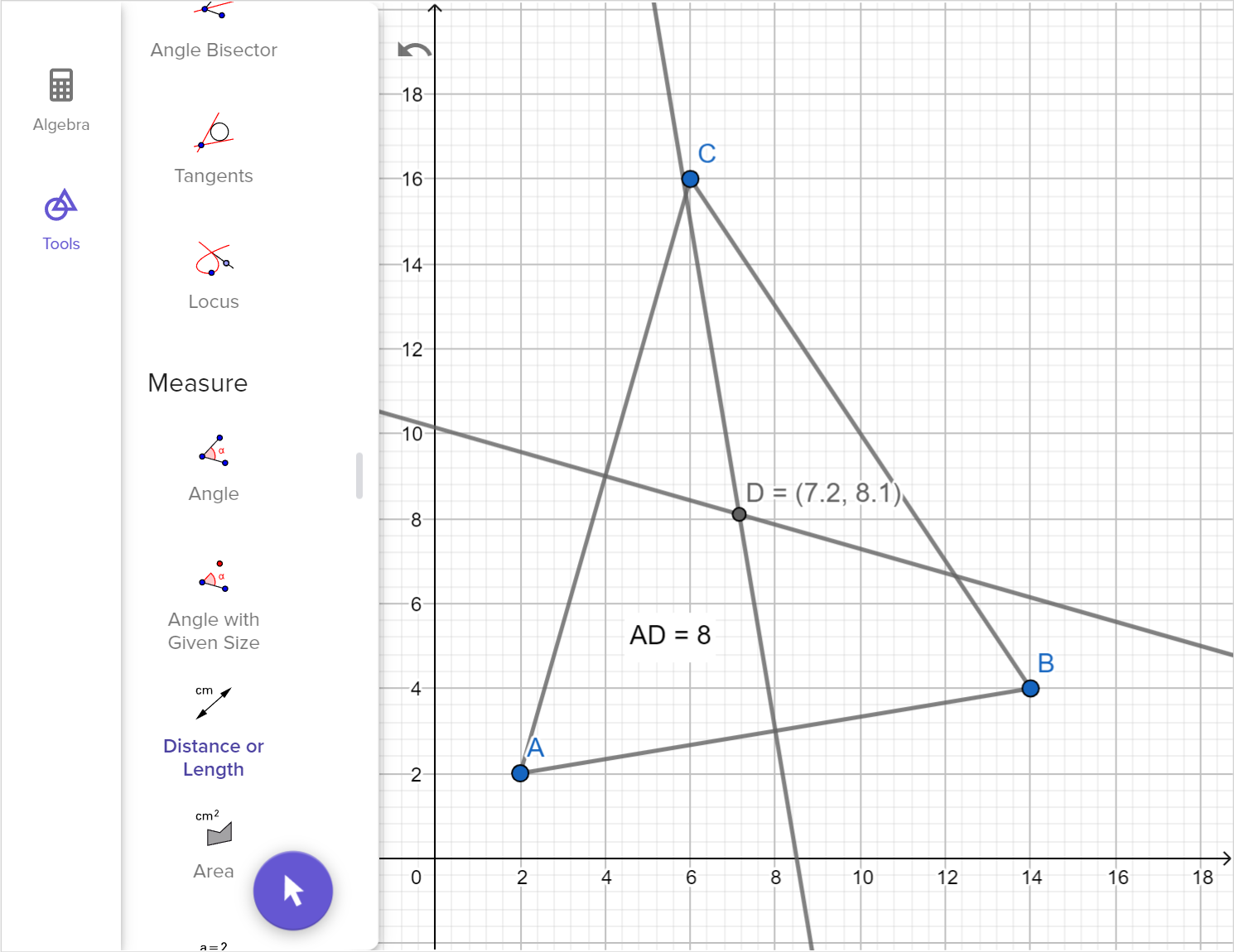
A cell phone tower is to be placed equally distant from the three locations shown of the map below.
Using technology, determine the coordinates of the location of the tower correct to one decimal place.
Find the distance from the tower to each location. Give your answer correct to one decimal place.
Example 3
Construct a circumscribed circle for the triangle below:
The circumcenter of a triangle the point of concurrency of the perpendicular bisectors of the triangle. It is also the center of the circumscribed circle of the triangle.
The circumcenter will lie inside of an acute triangle, outside of an obtuse triangle, and on the midpoint of the hypotenuse of a right triangle. The circumcenter will be equidistant from each vertex of a triangle.
To construct a circumscribed circle of a triangle, we can construct perpendicular bisectors on each segment. Then, we can draw a circle using their point of concurrency and a vertex on the triangle as the radius.
Angle bisectors
Recall that an angle bisector is a line, segment or ray that divides an angle into two congruent angles. When an angle bisector cuts an angle into two congruent angles, we can use the angle bisector theorem and the converse of the angle bisector theorem to solve problems in angles and triangles.
While we can construct a variety of angle bisectors and verify these theorems through experimentation, we don't yet have the knowledge to write a formal proof. We will formally prove the angle bisector theorem and its converse in a later lesson.
Exploration
Draw three different triangles and construct the angle bisectors of each side. Make sure each triangle is a different type: acute, obtuse, and right.
- What do you notice about the angle bisectors of the first triangle?
- Does what you noticed with the first triangle hold true for the other two?
The angle bisectors of a triangle intersect at a point of concurrency, called the incenter. The incenter is also the center of the inscribed circle of a triangle.
Examples
Example 4
Find x. Justify your answer.
Example 5
P is the incenter of the triangle.
Determine m \angle BAP.
Determine m \angle BPC.
Example 6
Draw a triangle and construct the inscribed circle.
Example 7
A landscaper used a coordinate plane to plan the layout of a garden. The plans include the three paths shown below, that pass through the points A \left(30,0\right), B \left(30,45\right) and C \left(5,26.25\right). The landscaper wants to place a fountain at an equal distance from each path.
How could they find the coordinates of the fountain?
What is the location of the fountain?
The incenter is the point of concurrency of the angle bisectors of a triangle. It is called the incenter because it is the center of the inscribed circle of the triangle.
The incenter will be equidistant from each side of a triangle.
To construct the inscribed circle of a triangle, we can two construct angle bisectors on two angles and a perpendicular bisector. Then, we can draw a circle using the incenter and the point where the perpendicular line crosses the triangle's side as the radius.