Topics
2. Parallel and Perpendicular Lines
topic badge
United States of America
Grades 9-12

2.03 Perpendicular lines

Lesson
Practice

Introduction

In lesson  2.02 Proving lines parallel  , we used angle relationships to prove that lines are parallel to each other. We will use angle relationships and other theorems here to prove that lines are perpendicular to each other and construct perpendicular lines here.

Proofs and constructions of perpendicular lines

Perpendicular lines

Two lines that intersect at right angles. Lines are denoted as being perpendicular by the symbol \perp.

Two intersecting lines with a right angle marking.
Midpoint

A point exactly halfway between the endpoints of a segment that divides it into two congruent line segments.

A line segment with endpoints A and C with a point B directly in the middle labeled Midpoint.

Exploration

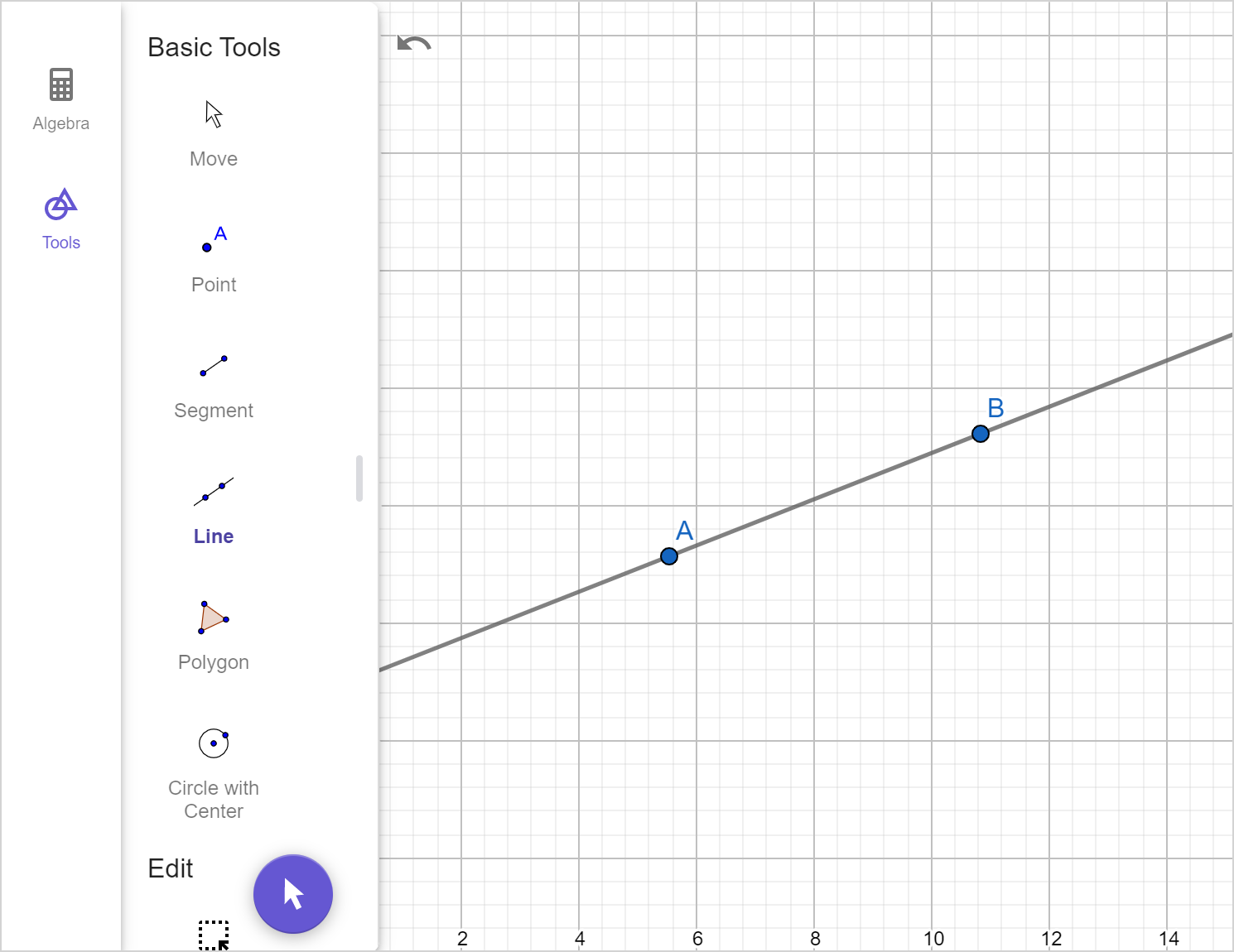
Drag points A, B, and P to change the lengths.

Loading interactive...
  1. What relationships in the diagram are always true? Can you explain why?

A point, line, or ray that is perpendicular to a line segment at its midpoint is a perpendicular bisector.

Perpendicular bisector theorem

If a point is on the perpendicular bisector of a line segment, then it is equidistant from the end points of the line segment.

Segment M N with a point P on M N. Another segment O P is drawn perpendicular to M N. Points Q, R, S and T are on O P. For each point, dashed segment are drawn from the point to M and N.

To construct a perpendicular line, we can use the following method:

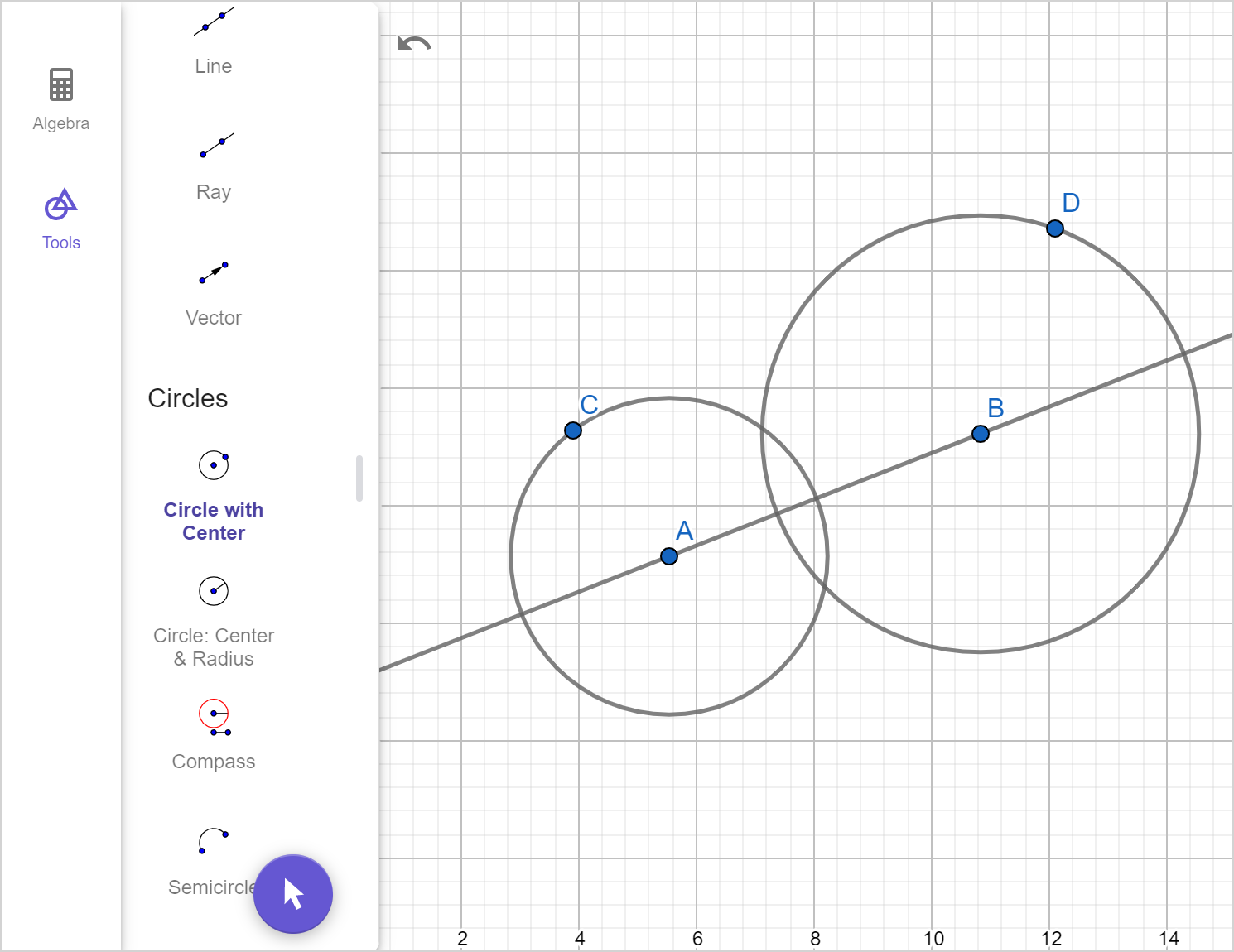
  1. Choose two points on a given line.

    A line with two points.

  2. Construct an arc centered at one of the points.

    A line with two points. An arc centered at one of the points is drawn.

  3. Construct an arc centered at the other point, such that this arc intersects the arc constructed in Step 2 at two distinct points.

    A line with two points. Two arcs centered at the points are drawn.

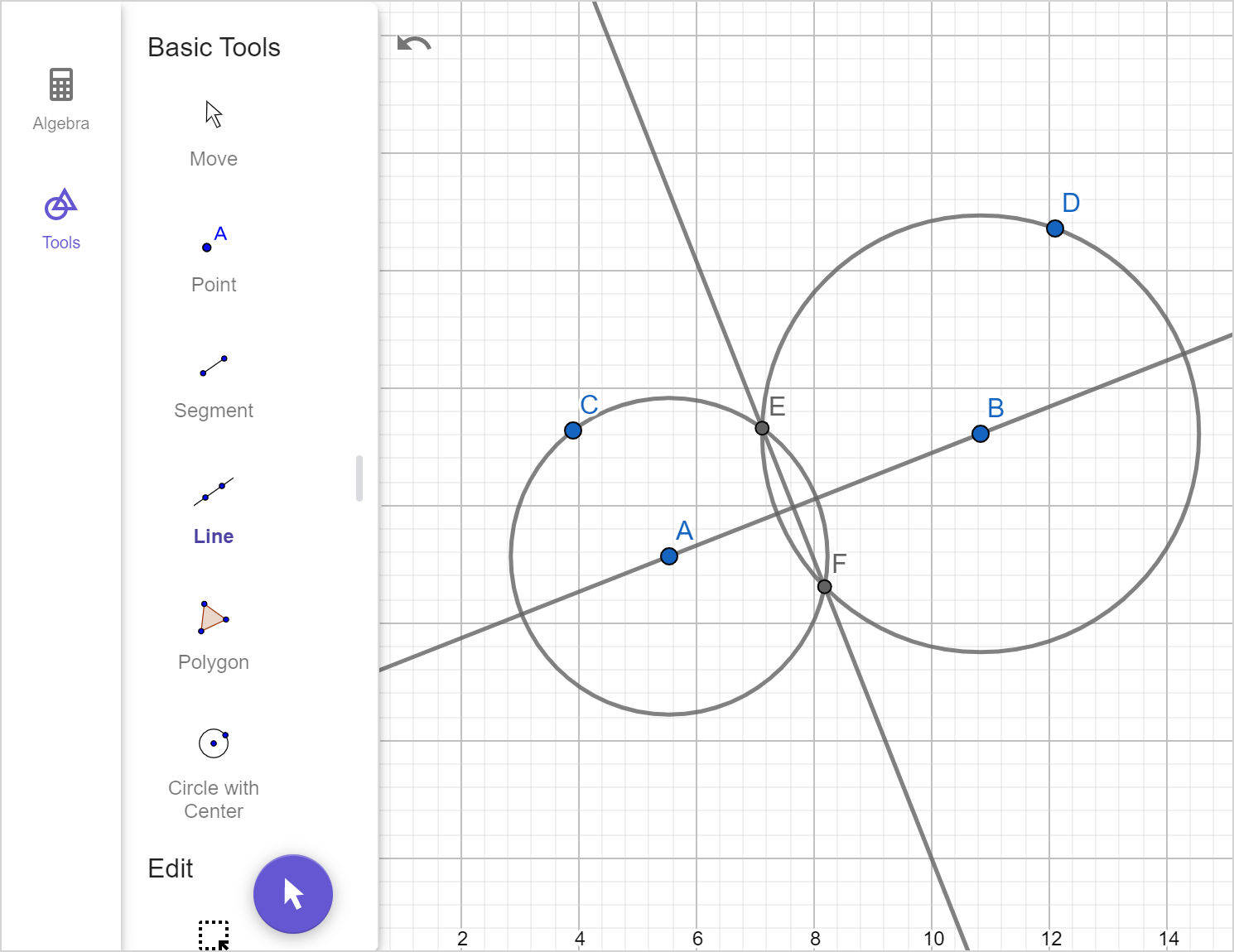
  4. Plot points where the two arcs intersect. Here we have used A and A'.

    A line with two points. Two arcs centered at the points are drawn. The points of intersections of the two arcs are labeled A and A prime.

  5. Construct the line \overleftrightarrow{AA'}. It is perpendicular to the line constructed in Step 1.

    A line with two points. Two arcs centered at the points are drawn. The points of intersections of the two arcs are labeled A and A prime. A line passing through A and A prime is drawn.

If we want the perpendicular line to pass through a particular point, we can adjust the radii of the compass so that both arcs pass through that point.

Examples

Example 1

Recall that the Pythagorean theorem states that given a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of its legs lengths.

Prove the perpendicular bisector theorem.

Worked Solution
Create a strategy

To prove this theorem, construct a segment \overline{PM} \perp \overline{AB} such that M is the midpoint of \overline{AB}.

Since both \triangle AMP and \triangle BMP are right angled triangles with AM=BM (given) and \overline{PM} common to both we can use the Pythagorean theorem and substitution to find the relationship between PA and PB.

Triangle A P B with point M on side A B. A segment is drawn from P to M perpendicular to A B. Segments A M and M B are congruent.
Apply the idea
To prove: PA=PB
StatementsReasons
1.AM=BMGiven
2.\triangle AMP is a right triangle\overline{PM}\perp\overline{AB}
3.\triangle BMP is a right triangle\overline{PM}\perp\overline{AB}
4.PA^{2}=AM^{2}+PM^{2}Pythagorean theorem in \triangle AMP
5.PB^{2}=BM^{2}+PM^{2}Pythagorean theorem in \triangle BMP
6.PB^{2}=AM^{2}+PM^{2}Substitution property of equality
7.PA^{2}=PB^{2}Transitive property of equality
8.PA=PBSquare root property

Example 2

Construct a proof of the following:

Given: m \angle1 = m \angle 2

Prove: l \perp m

Line l intersecting line m. Line m forms an angle labeled 1 with the left side of line l, and an angle labeled 2 with the right side of line l.
Worked Solution
Create a strategy

We can use a flow chart proof, two column proof, bulleted list, or paragraph proof to prove that l \perp m. For this proof, we will use a two column proof.

Apply the idea
To prove: l \perp m
StatementsReasons
1.m \angle1 = m \angle 2Given
2.\angle 1 and \angle 2 are supplementaryLinear pair theorem
3.m\angle1 + m\angle 2 = 180 \degreeDefinition of supplementary angles
4.m\angle1 + m\angle 1 = 180 \degreeSubstitution property of equality
5.m\angle1= 90 \degreeDivision property of equality
6.\angle 1 is a right angle and l \perp mDefinition of perpendicular lines

Example 3

Ludek is creating a shirt design on his computer. He wants to include some perpendicular lines as part of the design, but the program he is using doesn't measure angles so he can't construct them directly using a right angle.

The program Ludek is using can construct lines and circles accurately through or centered at points. Describe how Ludek could construct the perpendicular lines for his design.

Worked Solution
Create a strategy

One approach Ludek can use to construct perpendicular lines is by using dynamic technology software.

Apply the idea

  1. Use the 'Line' tool to construct a line through two points.

    A screenshot of the GeoGebra geometry tool showing the constructions described in step 1. Speak to your teacher for more details.

  2. Use the 'Circle with Center' tool to construct a circle about each point on the line, such that the circles intersect at two distinct points.

    A screenshot of the GeoGebra geometry tool showing the constructions described in step 2. Speak to your teacher for more details.

  3. Use the 'Line' tool once more to construct a line through the points of intersection of the circles. This line will be perpendicular to the first line.

    A screenshot of the GeoGebra geometry tool showing the constructions described in step 3. Speak to your teacher for more details.
Reflect and check

Notice that while we have constructed a perpendicular line, it is not a perpendicular bisector because the radii of the two circles used in the construction are not the same. Therefore, the line does not pass through the midpoint of \overline{AB}.

Example 4

Construct perpendicular bisector \overleftrightarrow{CD} through \overline{AB}.

Segment A B.
Worked Solution
Create a strategy

One approach to constructing the perpendicular bisector through \overline{AB} is using a compass and straightedge.

Apply the idea

1. Construct an arc centered at point A so that the arc is longer than half of \overline{AB}.

Segment A B. An arc centered at A is drawn.

2.Construct an arc centered at point B using the same compass setting, such that this arc intersects the arc constructed in Step 1 at two distinct points. Label the two points C and D.

Segment A B. Arcs centered at A and B are drawn.

3. Draw \overleftrightarrow{CD}. Label the point M where \overleftrightarrow{CD} intersects \overline{AB}. M is the midpoint of \overline{AB}.

Segment A B. Arcs centered at A and B are drawn. A line is drawn using the points of intersection of the two arcs. The point of intersection of A B and the line is labeled M.

\overleftrightarrow{CD}\perp \overline{AB} at the midpoint of \overline{AB}, so \overleftrightarrow{CD} is the perpendicular bisector of \overline{AB}.

Idea summary

We can use the relationships between angles to prove that lines are perpendicular. We can use various methods to construct perpendicular lines including technology and a compass and straightedge.

Solving problems with perpendicular lines

A particular type of transversal is one that is perpendicular to the lines that it intersects.

A pair of lines intersected by a transversal. The two lines form right angles with the transversal.

Using the converse of corresponding angles postulate, we can determine that the two lines intersected by the transversal are parallel (because both angles in any pair of corresponding angles will measure 90 \degree making them congruent).

When the transveral is perpendicular to the lines it intersect, we can get the following theorems relating parallel and perpendicular lines.

Perpendicular tranversal theorem

If a\perp c and a\parallel b, then b\perp c.

Parallel lines a and b intersecting line c. Lines a and b are perpendicular to c.
Converse of perpendicular transversal theorem

If a\perp c and b\perp c, then a\parallel b.

Parallel lines a and b intersecting line c. Lines a and b are perpendicular to c.

Examples

Example 5

Find the value of x that makes the diagram valid.

Line a intersects with line b, and line c intersects with line d. Lines a and c are parallel, as well as lines b and d. Lines a and b form a right angle. Lines c and d form an angle labeled x plus 38 degrees.
Worked Solution
Create a strategy

Using the perpendicular transversal theorem and its converse, we can conclude that the diagram is valid when a and c are perpendicular to b and d. This means that the angle of measure (x+38)\degree needs to be a right angle.

Apply the idea

To find the value of x that makes the diagram valid, we let:

x+38=90

Solving this equation gives us x=52, which is when the diagram will be valid.

Example 6

Consider the given relations between lines:

  • a\parallel b
  • b\perp d
  • c\perp d
a

Determine the relationship between the lines b and c. Justify your answer.

Worked Solution
Apply the idea

Using the converse of perpendicular transversal theorem, since b\perp d and c\perp d,we have that b \parallel c.

Reflect and check

We can use the given theorems to justify, but we can also check our reasoning by sketching a diagram.

Parallel horizontal lines a and b, a vertical line d, and another line c. Line d forms right angles with both b and c.

By extending some of these lines and using other theorems to show parallelism and perpendicularity, we can reach the same results.

b

Determine the relationship between the lines a and d. Justify your answer.

Worked Solution
Apply the idea

Since parallel relations are symmetric, since a \parallel b we can write that b\parallel a.

Using the perpendicular transversal theorem, since b\perp d and b\parallel a, we have that d\perp a.

Reflect and check

Since perpendicular relations are also symmetric, we can also write the relation as a\perp d.

Idea summary

The perpendicular transversal theorem and its converse help us draw conclusions about relationships between lines and solve problems.

  • The perpendicular transversal theorem states that if a \perp c and a \parallel b, then b \perp c.
  • The converse of perpendicular transversal theorem states that if a \perp c and b \perp c, then a \parallel b.

Outcomes

G.CO.A.1

Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.

G.CO.C.9

Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment's endpoints.

G.CO.D.12

Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.

What is Mathspace

About Mathspace