8.01 Comparing functions across representations
Introduction
We have learned about key features of functions in Algebra 1 and throughout Algebra 2. These key features also apply to functions that represent real-world contexts. This lesson aims to compare functions represented in different ways and determine which functions best model real-world phenomena.
Comparing functions across representations
Functions can be represented in a variety of ways, including equations, tables, and graphs. It is important to be able to compare functions whether they are represented in similar or different ways.
Useful information can usually be obtained by comparing key features of the functions. Remember that key features include:
Domain and range
Intercepts
End behavior
Rate of change
Maximum or minimum value(s)
Positive and negative intervals
Increasing and decreasing intervals
Asymptote(s)
Axis of symmetry
Recall the function families we have studied throughout Algebra 2:
Examples
Example 1
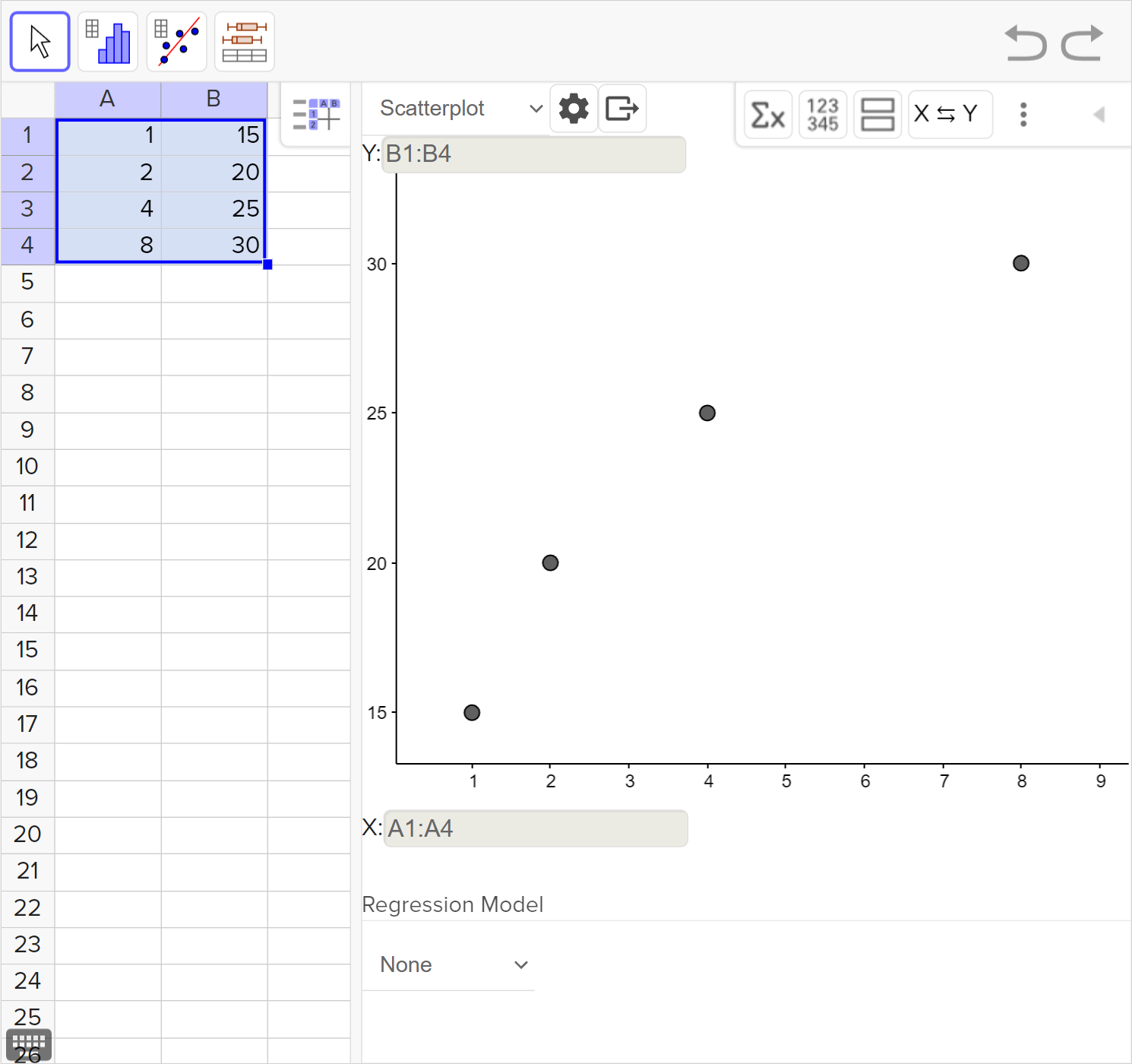
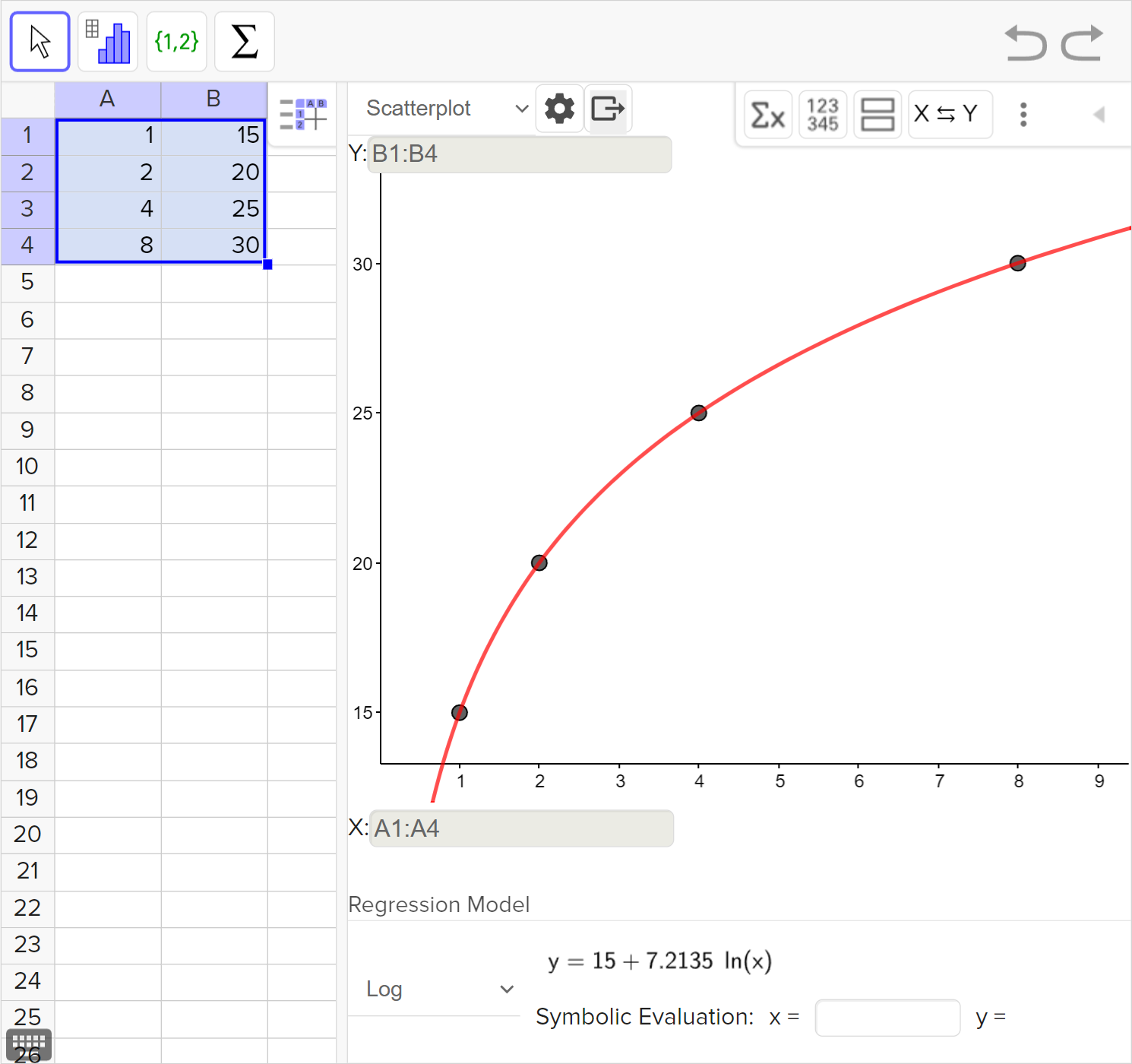
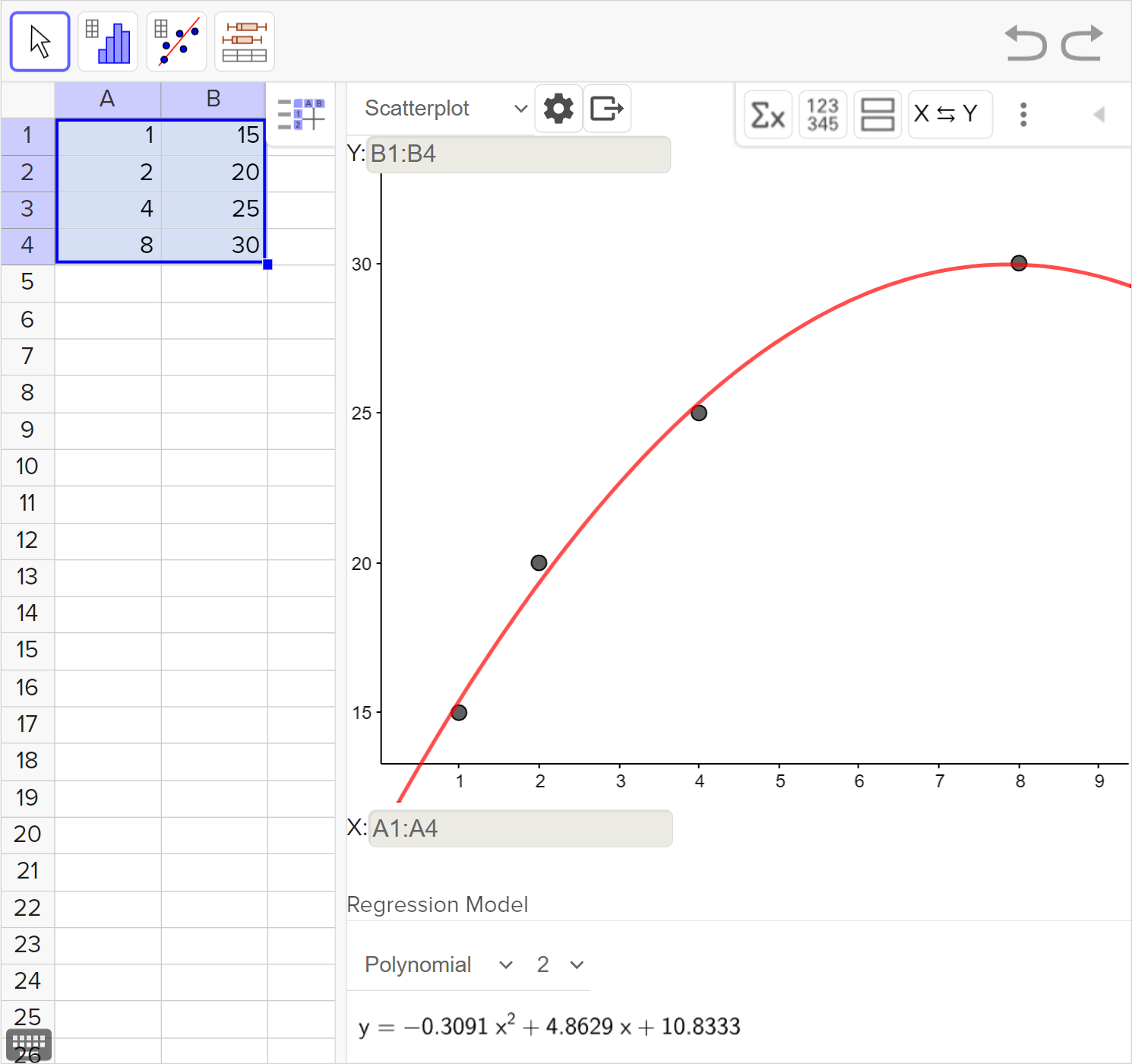
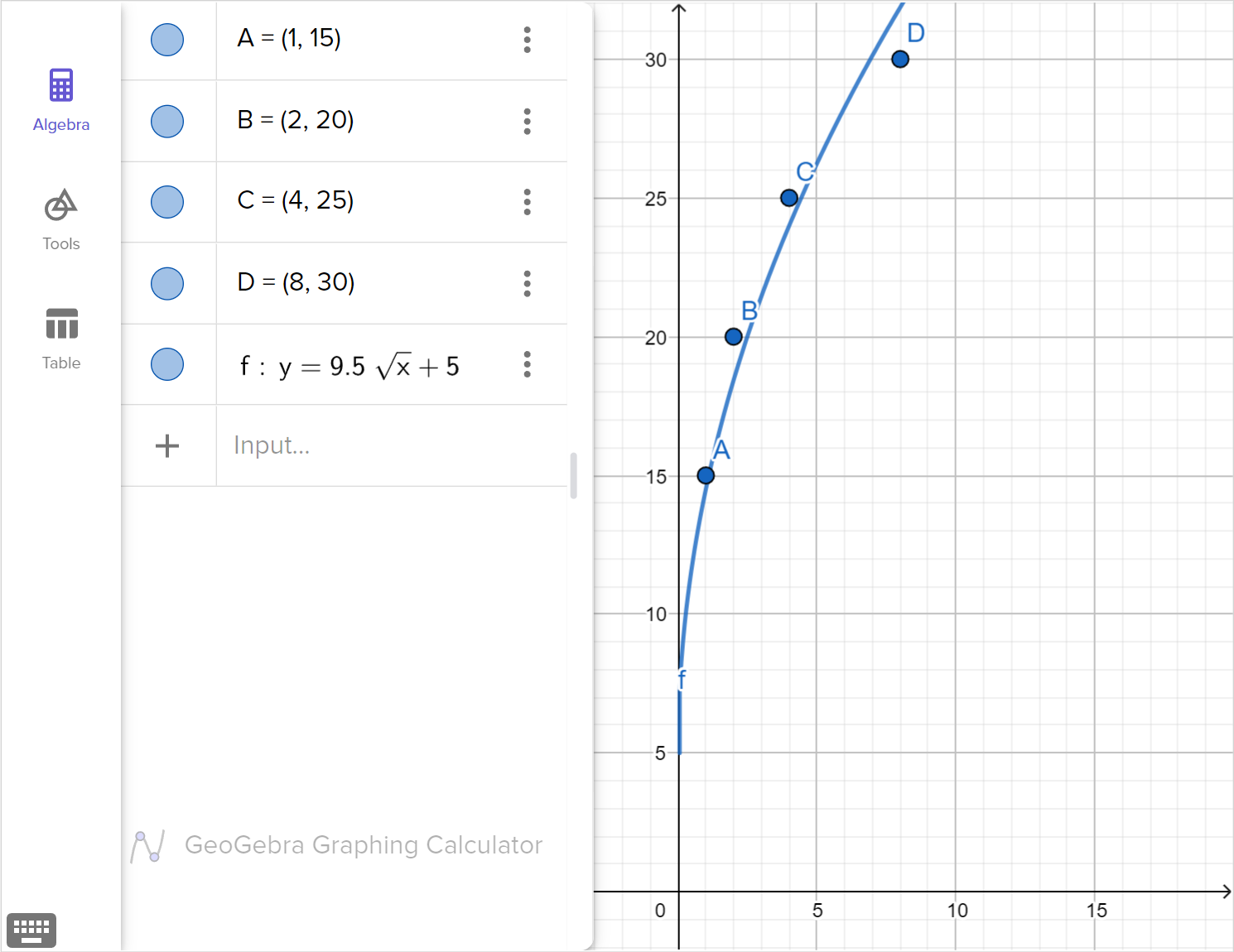
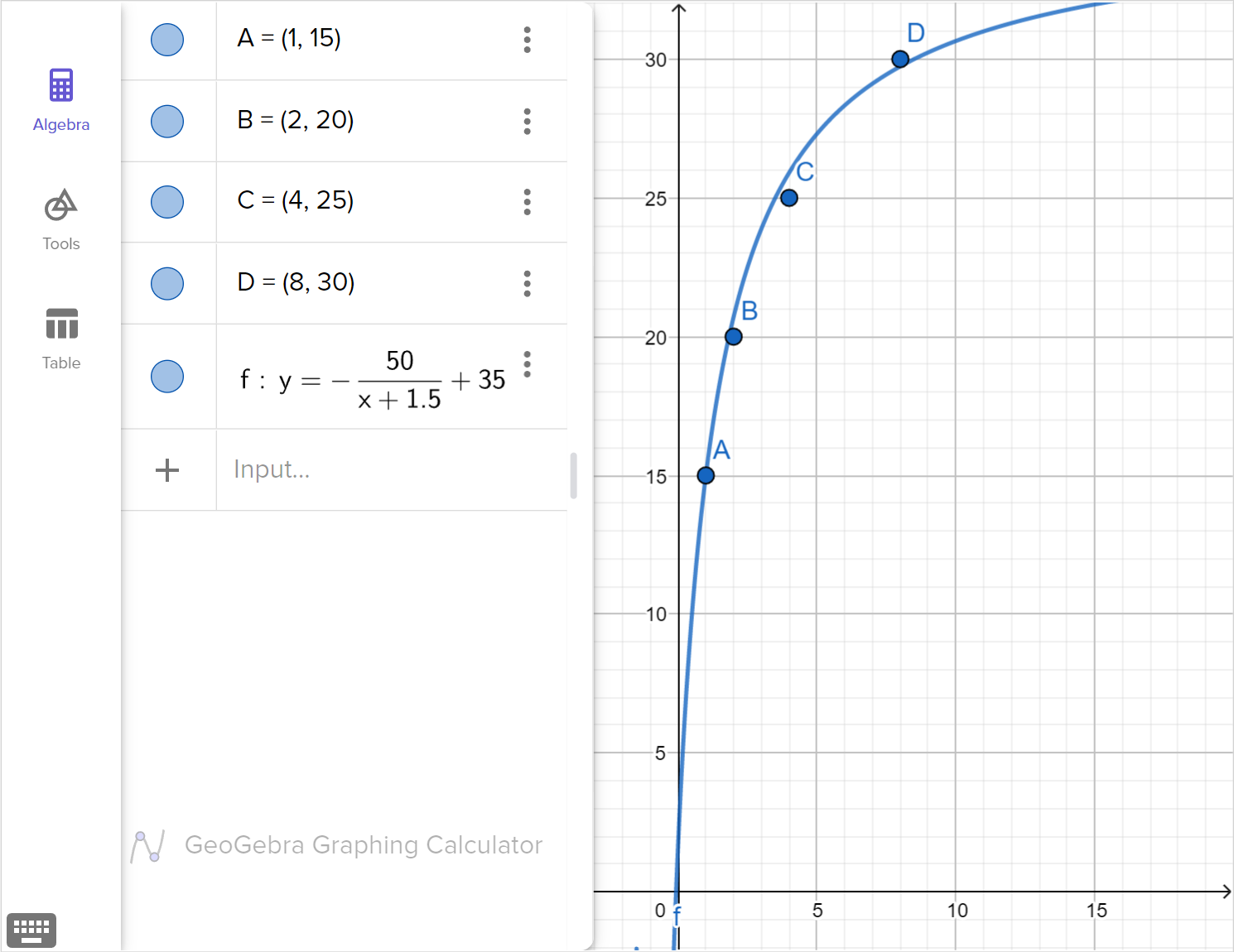
Nasrin decides to start doing home exercises and records the number of push-ups that they can do in one attempt at the end of a given week. Their results are shown in the table.
| Week | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| Push-ups | 15 | 20 | 25 | 30 |
Choose which of the following functions would model Nasrin's exercise chart best: a radical function, a rational function, quadratic function, or a logarithmic function.
State the number of push ups that Nasrin will be able to do after 16 weeks, according to the model you chose in part (a).
Example 2
The graph of function f \left(x \right) shown below follows the vertical height of Ameth's golf ball after being hit into the air and falling on the fairway:
The equation of function g \left(x \right) shown below follows the vertical height of Massiel's golf ball after being hit into the air and rolling through a sand trap, then out onto the green:g(x) = \begin{cases} 14 \sin \frac{3}{4}x, & 0 < x < 4 \\ \frac{1}{2} \left(x-6 \right) ^2, & 4 \leq x < 7.5 \\ -\frac{1}{4}x +3, & 7.5 \leq x < 12 \end{cases}
Determine whose ball is falling at a faster rate from 2 to 3 seconds.
Determine which part of the function g \left(x \right) shows the ball's vertical height in the sand trap.
Determine whose ball goes higher.
Real-world contexts can be modeled by various types of functions. We can compare different types of models for contextual situations using their key features:
Domain and range
Intercepts
End behavior
Rate of change
Maximum or minimum value(s)
Positive and negative intervals
Increasing and decreasing intervals
Asymptote(s)
Axis of symmetry