4.04 Modeling with polynomial functions (M)
Introduction
Throughout Algebra 1 and Geometry, we practiced modeling real-world situations with mathematics. In this lesson, we will dive into the first half of the modeling process, while also focusing on polynomial function models. When we model with mathematics, we work through the modeling cycle:
Each time we model a real-world situation, we should:
Identify the essential features of the problem
Create a model using a diagram, graph, table, equation or expression, or statistical representation
Analyze and use the model to find solutions
Interpret the results in the context of the problem
Verify that the model works as intended and improve the model as needed
Report on our findings and the reasoning behind them
Identifying the problem
Situations that require modeling are often broad and complex. There may be multiple ways to solve the problems and multiple solutions to the problems. Before we can determine a path to a solution, we often need to clarify the problem that needs to be solved.
To clarify the problem, we need to do the following:
Restate the problem to clarify what the model intends to measure, predict, and/or solve
Identify questions that need to be considered prior to answering the given problem
List factors that will affect the outcome
Research information needed to answer the problem
State assumptions
By making assumptions, you are narrowing the focus of the problem you are trying to solve and thus, simplifying the process for solving the problem.
For example, if you are asked to identify the best noise-canceling headphones on the market today, you will need to make assumptions about what the word "best" refers to. You may make an assumption that "best" refers to the clarity of the sound produced and the level of outside noise that can be heard. Someone else may assume it refers to the value for money in terms of sound quality, price, durability, and/or battery life. Various assumptions lead to different but valid outcomes.
Examples
Example 1
Design a model for a roller coaster that contains at least 3 peaks.
Identify the important factors that need to be considered when answering this question.
List assumptions that need to be made.
State a recommended plan for solving the problem, including any research that needs to be done to further clarify the problem.
A modeling problem is often open-ended with many unknowns. Our job is to research and brainstorm the problem, determine how a model can solve the problem, and make necessary assumptions to support our model.
Creating and analyzing a model
A model may take on different forms. Models can be presented as equations, graphs, tables, diagrams, and maps. In most modeling questions, you need to determine which function type and which form of the model would best represent the situation and answer the question. The key factor is that the model conveys the information in a way that is accessible.
A variable is used to represent a quantity in our problem that can take on many values. A parameter is a known value that may remain constant in the model. When creating a model, we need to define the independent and dependent variables and state any restrictions on those variables.
After creating a model, it is important to analyze whether the model accurately represents the situation in context. If the model is not an accurate representation, then we need to adjust the model or decide on a new type of model.
Examples
Example 2
Jax threw a ball into the air as hard as he could. The path of the ball was modeled by J\left(x\right)=-16x^2+47x+5 where x represents the horizontal distance of the ball in feet and J\left(x\right) represents the vertical height in feet. Jax's friend Cade then took the ball and threw it twice as far as Jax did. Assume the boys are the same age and height with similar athletic abilities.
Create a model for the path of the ball thrown by Cade.
Analyze the model you created to determine if it is a good fit for the situation. If it is a good fit, explain why. If it is not a good fit, adapt the model to better fit the situation.
Explain how Cade was able to throw the ball twice as far.
Example 3
Kala wants to build a fruit and vegetable garden in her family's backyard. To support her ambitions, her family bought 300\text{ ft} of fencing for her to use. Kala wants to separate the fruit from the vegetables, so her plan is to build an enclosure that is separated down the middle by a row of fence.
Kala plans to use all the available fencing to create her garden. She is debating between a circular and rectangular garden.
Create a model to represent the perimeter and area for each garden type. Define your variables and discuss any constraints.
Analyze your models to determine which type of garden Kala should make. Include the dimensions of the garden. Give mathematical and contextual arguments to defend your choice.
Example 4
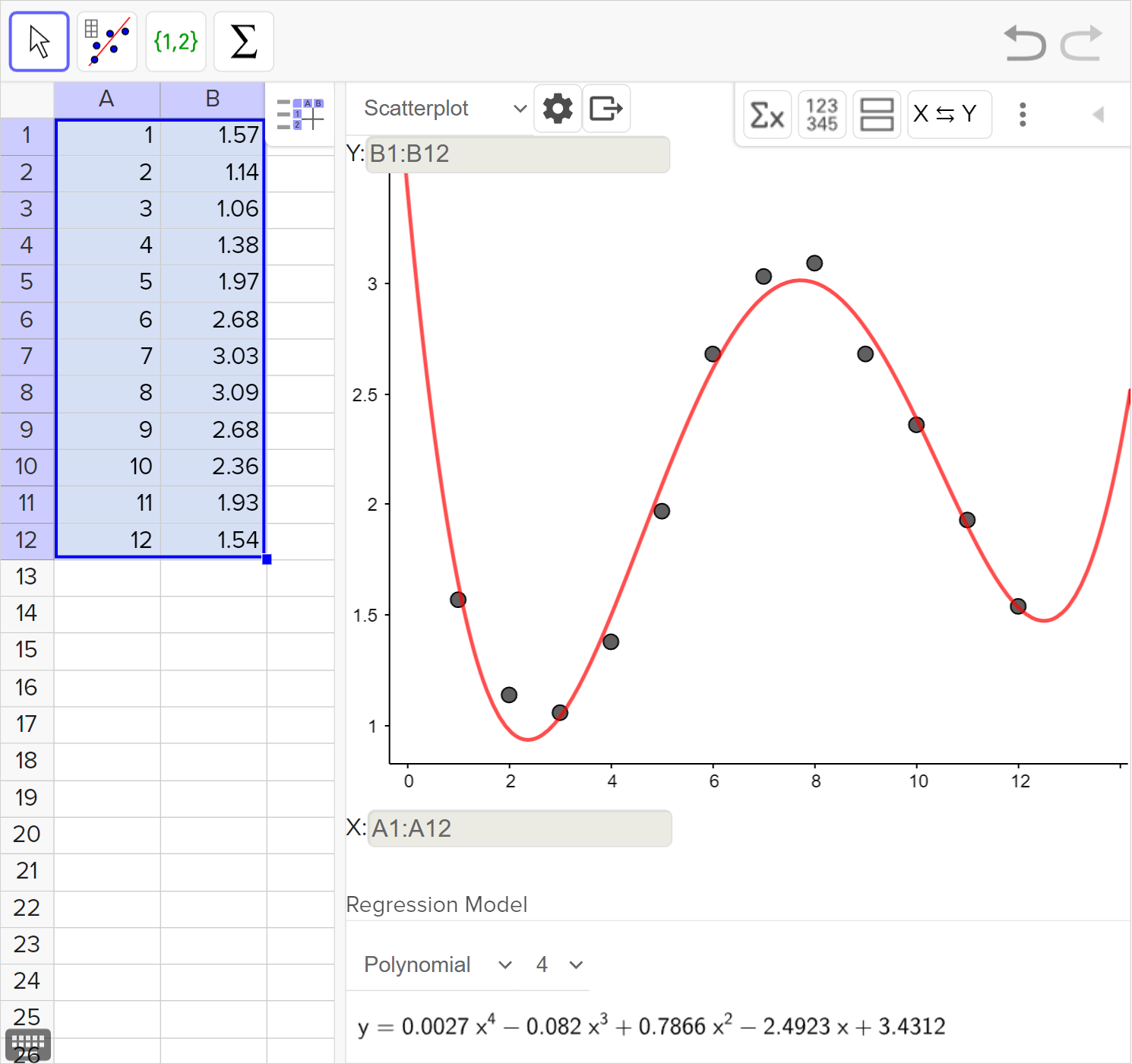
A city in Russia recorded the amount of rainfall in inches from March to December of a particular year. The results are shown in the table below.
| Month | \text{Mar} | \text{Apr} | \text{May} | \text{June} | \text{July} | \text{Aug} | \text{Sept} | \text{Oct} | \text{Nov} | \text{Dec} |
|---|---|---|---|---|---|---|---|---|---|---|
| Rainfall | 1.06 | 1.38 | 1.97 | 2.68 | 3.03 | 3.09 | 2.68 | 2.36 | 1.93 | 1.54 |
Explain which type of regression model you think best fits the data.
Two previously collected data points were accidentally overlooked when the table was created. The added data points are: \begin{aligned}\text{Jan }1.57\\\text{Feb }1.14\end{aligned} Explain how this affects the type of function you would choose to fit the data.
Create a regression model that best fits all the data from the full calendar year. Justify the reasoning for your choice of model.
The city council wants a report about the rainfall over the course of the year. Explain to the council what information the model created in part (c) can provide. Include any limitations of the model.
Models can be presented as equations, graphs, tables, diagrams, and maps. In most modeling problems involving functional relationships, you need to determine which function type and which form of the model would best represent the situation and answer the question.
When creating a model, we must always define the variables. After the model is created, we need to analyze the model in context. If the model does not make sense in context, does not fit the situation well, or does not give a complete picture, we can create a new, revised, or additional model.