5.01 Exponential functions
Introduction
A linear function can be used to describe relations that increase or decrease by a constant amount over time. However, many relations increase or decrease by different amounts over time. We will investigate one of those types of functions, called exponential functions, and explore the unique way in which the outputs change over time.
Characteristics of exponential functions
Exponential relationships include any relations where the outputs increase by a constant factor or decrease by a constant factor for consistent changes in x.
An exponential relationship can be modeled by a function with the independent variable in the exponent, known as an exponential function:
Exploration
Consider the following equations with a=1:
y=\left(5\right)^x
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | \dfrac{1}{25} | \dfrac{1}{5} | 1 | 5 | 25 |
y=\left(\dfrac{1}{5}\right)^x
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 25 | 5 | 1 | \dfrac{1}{5} | \dfrac{1}{25} |
y=\left(-5\right)^x
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | \dfrac{1}{25} | -\dfrac{1}{5} | 1 | -5 | 25 |
y=\left(1\right)^x
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 1 | 1 |
For each of the functions, think about the following questions:
- What happens to y as x increases?
- What is the y-intercept for each of the functions?
- Does the function have an x-intercept?
We can determine whether a function is exponential by dividing consecutive function values to see if they have a constant factor.
The base, or constant factor, is the number being multiplied repeatedly. It tells us how quickly the output values are growing or shrinking. We can find the base by dividing a term by the previous term, as shown below:
In this example, we see that the function is growing exponentially. A function grows exponentially when it increases by a constant factor.
Exponential functions change at a faster rate than linear functions. In the table below, we are adding 3 to each term, but the terms do not grow as quickly.
All exponential functions of the form y=ab^x have the following features in common:
- The domain is -\infty <x<\infty.
- The y-intercept is at (0,a).
- There is a horizontal aysmptote at y=0.
An exponential function can get infinitely close to an asymptote, but it can never cross it. This means that an exponential function of this form will not have an x-intercept.
Examples
Example 1
Consider the table of values for the function y = 2\left(\dfrac{1}{3}\right)^{ x }.
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 486 | 162 | 54 | 18 | 6 | 2 | \dfrac{2}{3} | \dfrac{2}{9} | \dfrac{2}{27} | \dfrac{2}{81} | \dfrac{2}{243} | \dfrac{2}{59\,049} |
Describe the behavior of the function as x increases.
Determine the y-intercept of the function.
State the domain of the function.
State the range of the function.
Example 2
A large puddle of water starts evaporating when the sun shines directly on it. The amount of water in the puddle over time is shown in the table.
| Hours since sun came out | Volume in mL |
|---|---|
| 0 | 1024 |
| 1 | 512 |
| 2 | 256 |
| 3 | |
| 4 | 64 |
| 5 |
Given that the relationship is exponential, complete the table of values.
Describe the relationship between time and volume.
The base of the exponent is the constant factor, or the number being multiplied repeatedly. We can find it by dividing one output by the previous output.
All exponential functions of the form y=ab^x have the following features in common:
- The domain is -\infty <x<\infty.
- The y-intercept is at (0,a).
- There is a horizontal asymptote at y=0.
Graphs of exponential functions
To draw the graph of an exponential function, we can use a variety of strategies, including:
- Completing a table of values for the function and drawing the curve through the points found
- Using technology, such as a physical or online graphing calculator
- Identifying key features from the equation
An exponential function could also have a leading coefficient which would be in the form:
The y-intercept is the value of a. We can check this by substituting x=0 in the function: y=ab^0. Since b^0=1, the y-intercept is (0,a).
Exploration
Move the sliders for a and b to see how the base and the exponent affect the graph of the exponential function.
- What are the possible values of a and b?
- What happens to the graph as b increases?
- What happens to the graph as a increases?
For exponential functions, the base must be a positive value other than 1. When 0<b<1, the function is decreasing. When b>1, the function is increasing.
The leading coefficient, a, can be any real number, and it determines the range of the function. When a>0, the range is y>0. When a<0, the range is y<0.
The value of a is the y-intercept, but it also affects the range of the function and tells us more about the rate of change.
Examples
Example 3
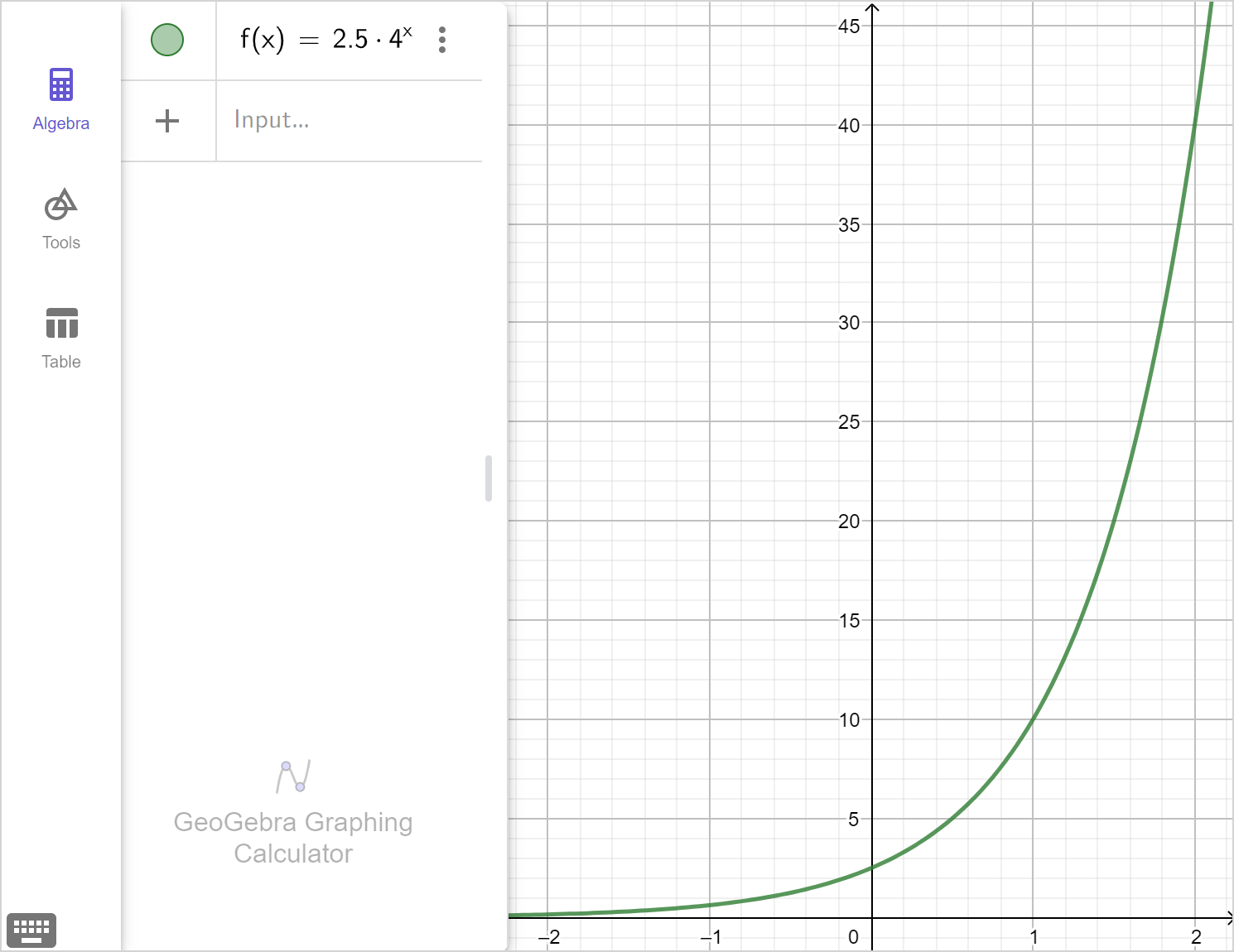
Consider the exponential function y=2.5\left(4\right)^x.
Draw the graph of the function.
Check the graph from part (a) using technology.
Example 4
Consider the exponential functions f\left(x\right)=2\left(\dfrac{1}{3}\right)^{x} and g\left(x\right)=3\left(\dfrac{1}{2}\right)^{x}.
Using a table of values, draw the graph of f\left(x\right) and g\left(x\right) on the same plane.
Determine which function is decreasing at a slower rate.
Example 5
Consider the following exponential functions:
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| g(x) | -9 | -3 | -1 | -\dfrac{1}{3} | -\dfrac{1}{9} |
Determine which function increases at a slower rate.
Identify the y-intercept for each function.
We can use the y-intercept and the constant factor to graph an exponential function in the form y=ab^x and identify key features:
- When a>0 and b>1, the function is increasing at an increasing rate.
- When a>0 and 0<b<1, the function is decreasing at a decreasing rate.
- When a<0 and b>1, the function is decreasing at an increasing rate.
- When a<0 and 0<b<1, the function is increasing at a decreasing rate.
- When a>0, the range is y>0.
- When a<0, the range is y<0.