25.02 Addition, subtraction and scalar multiplication
Geometric addition and subtraction of vectors (Extended)
The triangle law for addition
To add vectors we can use the triangle law. We put the tail of the second vector on the tip of the first vector. The resultant vector (the addition of the two vectors) is the vector that reaches from the initial point of the first vector to the terminal point of the second.
Worked example
Example 1
Add the two vectors $\mathbf{u}$u and $\mathbf{v}$v shown below using the triangle law:

Think: To add together, we reposition vector $\mathbf{v}$v so that the tail of $\mathbf{v}$v, is positioned at the tip of $\mathbf{u}$u
Do:

The resultant vector is the vector that extends from the beginning of $\mathbf{u}$u, and ends at the tip of $\mathbf{v}$v:

$\mathbf{u}+\mathbf{v}=\mathbf{w}$u+v=w where $\mathbf{w}$w is the vector that completes the triangle from the tail of $\mathbf{u}$u to the tip of $\mathbf{v}$v

Practice questions
Question 1
Which vector is the result of $a+b$a+b?
$c$c
A$d$d
B
Question 2
Consider the two vectors $a$a and $b$b, as graphed below.
Plot the result of $a+b$a+b on the same axes.
Loading Graph...Now plot the result of $b+a$b+a.
Loading Graph...Are the two resulting vectors $a+b$a+b and $b+a$b+a equal?
Yes
ANo
B
The triangle law for subtraction (Extended)
Subtracting vectors combines the ideas of negative vectors and addition. A negative vector has same size but opposite direction. This means that the concept of subtracting a vector is the same as adding its negative.
That is:
$\mathbf{u}-\mathbf{v}=\mathbf{u}+\left(-\mathbf{v}\right)$u−v=u+(−v)
Worked example
Example 2
Given the vectors $\mathbf{u}$u and $\mathbf{v}$v below, find $\mathbf{u}-\mathbf{v}$u−v:
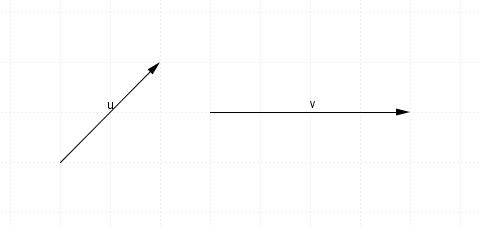
Think: We need to add the negative of $\mathbf{v}$v to $\mathbf{u}$u.
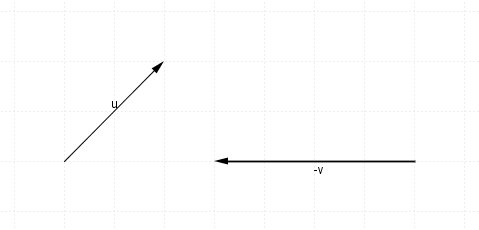
Do: $-\mathbf{v}$−v will look like this, (same size as $\mathbf{v}$v, just the opposite direction):
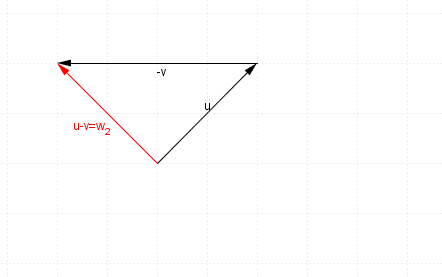
And hence $\mathbf{u}-\mathbf{v}$u−v, or $\mathbf{u}+-\mathbf{v}$u+−v will look like this:
Here are both the addition and subtraction of the two vectors to compare on the one diagram:
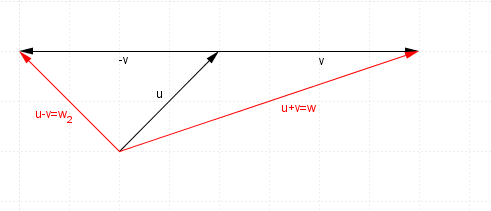
For two vectors $\mathbf{u}$u and $\mathbf{v}$v:
$\mathbf{u}-\mathbf{v}=\mathbf{u}+-\mathbf{v}$u−v=u+−v

Algebraic addition and subtraction of vectors
Column vectors and ordered pairs
Using column vector notation or ordered pairs we can add and subtract any number of vectors algebraically by adding or subtracting the corresponding elements together.
Worked example
Example 3
Add the two vectors $\mathbf{u}=\binom{-2}{7}$u=(−27) and $\mathbf{v}=\binom{8}{2}$v=(82) using algebraic methods.
Think: We can add these vectors algebraically by adding the individual corresponding elements of the vectors.
Do:
| $\mathbf{u}+\mathbf{v}$u+v | $=$= | $\binom{-2}{7}+\binom{8}{2}$(−27)+(82) |
| $\mathbf{u}+\mathbf{v}$u+v | $=$= | $\binom{-2+8}{7+2}$(−2+87+2) |
| $\mathbf{u}+\mathbf{v}$u+v | $=$= | $\binom{6}{9}$(69) |
For $\mathbf{u}=\binom{a}{b}$u=(ab) and $\mathbf{v}=\binom{c}{d}$v=(cd):
$\mathbf{u}+\mathbf{v}=\binom{a+c}{b+d}$u+v=(a+cb+d)
$\mathbf{u}-\mathbf{v}=\binom{a-c}{b-d}$u−v=(a−cb−d)
Practice question
Question 3
| Consider the vectors $A$A$=$= |
|
, $B$B$=$= |
|
and $C$C$=$= |
|
. |
$A+B$A+B $=$= $\editable{}$ $\editable{}$ $B+C$B+C $=$= $\editable{}$ $\editable{}$ $A+B+C$A+B+C $=$= $\editable{}$ $\editable{}$
Scalar multiplication of vectors
Geometrical methods (Extended)
As a scalar is a quantity that is magnitude only (no direction), its effect on a vector when multiplying is to increase the magnitude of the vector. It does not alter its direction.
Algebraic methods - column vectors
When multiplying column vectors by a scalar quantity we multiply each element by the quantity.
Worked example
Example 4
Given the two vectors $\mathbf{u}=\binom{-2}{7}$u=(−27) and $\mathbf{v}=\binom{8}{2}$v=(82) calculate:
(a) $3\mathbf{u}$3u
(b) $-2\mathbf{u}$−2u
(c) $4\mathbf{u}-\mathbf{v}$4u−v
Think: We can do these calculations by multiplying each element of the column vector by the scalar quantity.
Do:
(a)
| $3\mathbf{u}$3u | $=$= | $3\times\binom{-2}{7}$3×(−27) |
| $\mathbf{u}+\mathbf{v}$u+v | $=$= | $\binom{-6}{21}$(−621) |
(b)
| $-2\mathbf{v}$−2v | $=$= | $-2\times\binom{8}{2}$−2×(82) |
| $\mathbf{u}+\mathbf{v}$u+v | $=$= | $\binom{-16}{-4}$(−16−4) |
(c)
| $4\mathbf{u}-\mathbf{v}$4u−v | $=$= | $4\times\binom{-2}{7}-\binom{8}{2}$4×(−27)−(82) |
| $4\mathbf{u}-\mathbf{v}$4u−v | $=$= | $\binom{-8}{28}-\binom{8}{2}$(−828)−(82) |
| $4\mathbf{u}-\mathbf{v}$4u−v | $=$= | $\binom{0}{30}$(030) |
For $\mathbf{u}=\binom{a}{b}$u=(ab):
$k\mathbf{u}=\binom{ka}{kb}$ku=(kakb)
Practice questions
Question 4
Consider the vectors shown below.
|
Loading Graph... |
Loading Graph... |
|
Loading Graph... |
Loading Graph... |
Which vector is equivalent to $2a$2a?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $\frac{1}{4}b$14b?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $-a$−a?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $-\frac{1}{2}d$−12d?
$a$a
A$b$b
B$c$c
C$d$d
D
Question 5
| Let $a$a$=$= |
|
. Using the origin as the starting point, plot the following vectors: |
$3a$3a
Loading Graph...$-2a$−2a
Loading Graph...$\frac{1}{2}a$12a
Loading Graph...