4.05 Quadratic functions
Key features
Previously, key features of linear equations have been explored including the gradient, the $x$x-intercept, and the $y$y-intercept. The graph of a quadratic equation is a parabola and is a curved or concave shape (either concave up or down, depending on the equation). The following sections describe the key features of a parabola.
Intercepts
The $x$x-intercepts are where the parabola crosses the $x$x-axis. This occurs when $y=0$y=0.
The $y$y-intercept is where the parabola crosses the $y$y-axis. This occurs when $x=0$x=0.
These intercepts are shown in the picture below:
Recall that there may be one or two or even no $x$x-intercepts:
Maximum and minimum values
Maximum or minimum values are also known as the turning points, and they are found at the vertex of the parabola.
 |
 |
|
Parabolas that are concave up have a minimum value. This means the $y$y-value will never go under a certain value. In the example above, the range is $y\ge-15$y≥−15. |
Parabolas that are concave down have a maximum value. This means the $y$y-value will never go over a certain value. In the example above, the range is $y\le15$y≤15. |
Axis of symmetry
Maximum and minimum values occur on a parabola's axis of symmetry. This is the vertical line that evenly divides a parabola into two sides down the middle. Using the general form of the quadratic $y=ax^2+bx+c$y=ax2+bx+c, substitute the relevant values of $a$a and $b$b into the following equation:
$x=\frac{-b}{2a}$x=−b2a
Does it look familiar? This is part of the quadratic formula. It is the half-way point between the two solutions.
The gradient of a curve
Positive and negative gradients were previously explored for straight lines. If we draw the tangent line to a curve at a particular point we can estimate the gradient of a curve. A parabola has a positive gradient in some places and negative gradient in others. The parabola's maximum or minimum value, at which the gradient is $0$0, is the division between the positive and negative gradient regions. Hence, why it is also called the turning point.
Look at the picture below. One side of the parabola has a positive gradient, there is a turning point with a zero gradient, and the other side of the parabola has a negative gradient.
In this particular graph, the gradient is positive when $x<1$x<1 and the parabola is increasing for these values of $x$x. Similarly, the gradient is negative when $x>1$x>1, and for these values of $x$x, the parabola is decreasing.
Practice questions
Question 1
Examine the given graph and answer the following questions.
What are the $x$x values of the $x$x-intercepts of the graph? Write both answers on the same line separated by a comma.
What is the $y$y value of the $y$y-intercept of the graph?
What is the minimum value of the graph?
Question 2
Examine the attached graph and answer the following questions.
What is the $x$x-value of the $x$x-intercept of the graph?
What is the $y$y value of the $y$y-intercept of the graph?
What is the absolute maximum of the graph?
Determine the interval of $x$x in which the graph is increasing.
Give your answer as an inequality.
Graphing quadratics
As for linear equations, there are a number of forms for graphing quadratic functions:
General Form: $y=ax^2+bx+c$y=ax2+bx+c
Factored or $x$x-intercept form: $y=a\left(x-\alpha\right)\left(x-\beta\right)$y=a(x−α)(x−β)
Turning point form: $y=a\left(x-h\right)^2+k$y=a(x−h)2+k
Each form has an advantage for different key features that can be identified quickly. However, for each form, the role of $a$a remains the same.
That is:
- If $a<0$a<0 then the quadratic is concave down
- If $a>0$a>0 then the quadratic is concave up
- The larger the magnitude of $a$a, the narrower the curve
The following are examples of how to find all the key features for each form.
Graphing from turning point form
$y=a\left(x-h\right)^2+k$y=a(x−h)2+k
- This form is given this name as the turning point can be read directly from the equation: $(h,k)$(h,k)
- Obtain this graph from the graph of $y=x^2$y=x2, by dilating (stretching) the graph by a factor of $a$a from the $x$x-axis, then translating the graph $h$h units horizontally and $k$k units vertically
- The axis of symmetry will be at $x=h$x=h
- The $y$y-intercept can be found by substituting $x=0$x=0 into the equation
- The $x$x-intercept can be found by substituting $y=0$y=0 into the equation and rearranging
Practice questions
Question 3
Consider the equation $y=-\left(x+2\right)^2+4$y=−(x+2)2+4.
Find the $x$x-intercepts. Write all solutions on the same line, separated by a comma.
Find the $y$y-intercept.
Determine the coordinates of the vertex.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Graph the equation.
Loading Graph...
Question 4
Consider the equation $y=\left(x-3\right)^2+4$y=(x−3)2+4.
Does the graph have any $x$x-intercepts?
No
AYes
BFind the $y$y-intercept.
Determine the coordinates of the vertex.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Graph the equation.
Loading Graph...
Graphing from factored form
$y=a\left(x-\alpha\right)\left(x-\beta\right)$y=a(x−α)(x−β)
- From this form, read the $x$x-intercepts directly: $(\alpha,0)$(α,0) and $(\beta,0)$(β,0). If $y=0$y=0, solve the equation using the null factor law.
- The axis of symmetry will be at the $x$x-coordinate midway between the two $x$x-intercepts. Alternatively, expand this equation to general form and then use the formula for the axis of symmetry: $x=\frac{-b}{2a}$x=−b2a.
- The axis of symmetry is also the $x$x-coordinate of the turning point. Substitute this value into the equation then find the $y$y-coordinate of the turning point.
- The $y$y-intercept can be found by substituting $x=0$x=0 into the equation
Practice question
Question 5
Consider the parabola $y=\left(x+1\right)\left(x-3\right)$y=(x+1)(x−3).
Find the $y$y value of the $y$y-intercept.
Find the $x$x values of the $x$x-intercepts.
Write all solutions on the same line separated by a comma.
State the equation of the axis of symmetry.
Find the coordinates of the vertex.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Graph the parabola.
Loading Graph...
Graphing from general form
$y=ax^2+bx+c$y=ax2+bx+c
- From this form, read the $y$y-intercept directly: $(0,c)$(0,c)
- Find the axis of symmetry using the formula: $x=\frac{-b}{2a}$x=−b2a
- The axis of symmetry is also the $x$x-coordinate of the turning point. Substitute this value into the equation, then find the $y$y-coordinate of the turning point.
- The $x$x-intercept can be found by substituting $y=0$y=0 into the equation and then using one of the methods for solving quadratics, such as factorising or the quadratic formula, to find the zeros (x - intercepts) of the equation.
Alternatively, use the method of completing the square to rewrite the quadratic in turning point form.
Sometimes, the solutions for a quadratic may be asked for. This is referring to the $x$x-intercepts which satisfy the equation $y=0$y=0. The solutions are sometimes called the roots of the equation.
Practice questions
Question 6
Consider the quadratic function $y=x^2+2x-8$y=x2+2x−8.
Determine the $x$x-value(s) of the $x$x-intercept(s) of this parabola. Write all answers on the same line separated by commas.
Determine the $y$y-value of the $y$y-intercept for this parabola.
Determine the equation of the vertical axis of symmetry for this parabola.
Find the $y$y-coordinate of the vertex of the parabola.
Draw a graph of the parabola $y=x^2+2x-8$y=x2+2x−8.
Loading Graph...
question 7
A parabola has the equation $y=x^2+4x-1$y=x2+4x−1.
Express the equation of the parabola in the form $y=\left(x-h\right)^2+k$y=(x−h)2+k by completing the square.
Find the $y$y-intercept of the curve.
Find the vertex of the parabola.
Vertex $=$= $\left(\editable{},\editable{}\right)$(,)
Is the parabola concave up or down?
Concave up
AConcave down
BHence plot the curve $y=x^2+4x-1$y=x2+4x−1
Loading Graph...
Question 8
Consider the graph of the function $f\left(x\right)=-x^2-x+6$f(x)=−x2−x+6.
Using the graph, write down the solutions to the equation $-x^2-x+6=0$−x2−x+6=0.
If there is more than one solution, write the solutions separated by commas.
Graphing quadratics using technology
Technology can be used to graph and find key features of a quadratic function. We may need to use our knowledge of the graph or calculate the location of some key features to find an appropriate view window.
Practice question
Question 9
Use your calculator or other handheld technology to graph $y=4x^2-64x+263$y=4x2−64x+263.
Then answer the following questions.
What is the vertex of the graph?
Give your answer in coordinate form.
The vertex is $\left(\editable{},\editable{}\right)$(,)
What is the $y$y-intercept?
Give your answer in coordinate form.
The $y$y-intercept is $\left(\editable{},\editable{}\right)$(,)
Let's explore how a quadratic function changes using the applet below. What happens when we change the sliders for dilation, reflection, vertical translation and horizontal translation? Can you describe what changes these values make to the quadratic function?
These movements are called transformations. Transform means change, and these transformations change the simple quadratic $y=x^2$y=x2 into other quadratics by moving (translating), flipping (reflecting) and making the graph appear more or less steep (dilating).
By using the above applet, step through these instructions:
- Start with the simple quadratic $y=x^2$y=x2
- Dilate the quadratic by factor of $2$2
- Reflect on the $x$x-axis
- Translate vertically by $2$2 and horizontally by $-3$−3 units
How has the graph changed? Can you visualise the changes without using the applet? What is the resulting equation?
Equations and Transformations of Quadratics
Transforming a quadratic will change its equation. Here are some of the most common types of quadratic equations, and what they mean with regards to the transformations that have occurred.
$y=ax^2$y=ax2
If $a<0$a<0 (that is, $a$a is negative) then we have a reflection parallel to the $x$x-axis. It's like the quadratic has been flipped upside down.
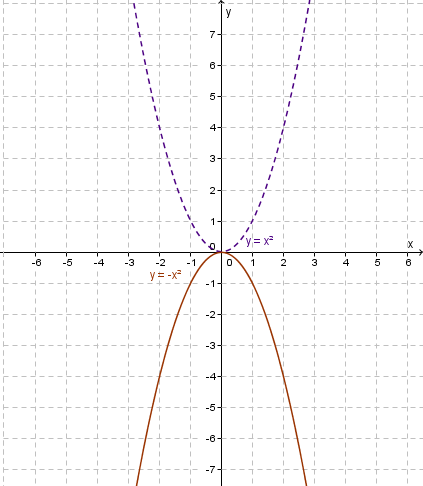
Shows the reflection of
$y=x^2$y=x2 to $y=-x^2$y=−x2
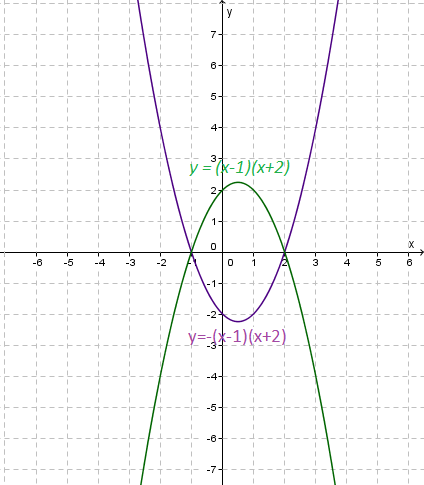
Shows the reflection of
$y=\left(x-1\right)\left(x+2\right)$y=(x−1)(x+2) to $y=-\left(x-1\right)\left(x+2\right)$y=−(x−1)(x+2)
$y=ax^2$y=ax2
This is a quadratic that has been dilated vertically by a factor of $a$a.
If $\left|a\right|>1$|a|>1 then the graph is steeper than $y=x^2$y=x2.
If $\left|a\right|<1$|a|<1 then the graph is flatter than $y=x^2$y=x2.
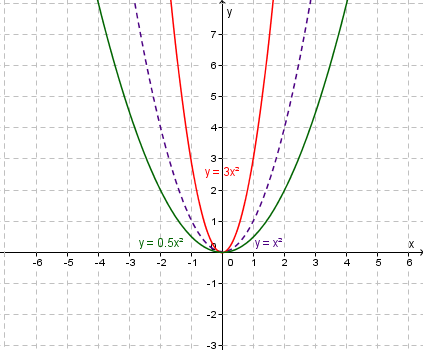
Dilation of $y=x^2$y=x2 to $y=3x^2$y=3x2 and $y=\frac{1}{2}x^2$y=12x2
$y=ax^2+k$y=ax2+k
In the graph $y=ax^2+k$y=ax2+k, the quadratic has been vertically translated by $k$k units.
If $k>0$k>0 then the translation is up.
If $k<0$k<0 then the translation is down.
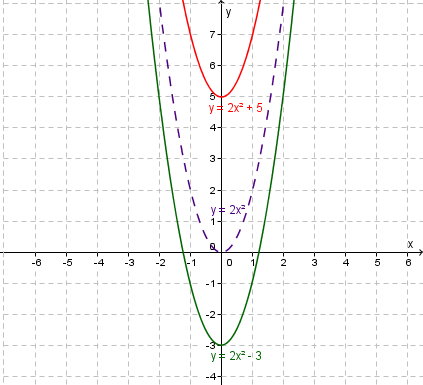
Vertical translation.
Showing one curve $y=2x^2+5$y=2x2+5 having a vertical translation of up $5$5 units, and
another $y=2x^2-3$y=2x2−3 having a vertical translation of down $3$3 units.
$y=\left(x-h\right)^2$y=(x−h)2
The $h$h indicates the horizontal translation.
If $h>0$h>0, that is the factor in the brackets is $\left(x-h\right)$(x−h) than we have a horizontal translation of $h$h units right.
If $h<0$h<0, that is the factor in the brackets is $\left(x-\left(-h\right)\right)=\left(x+h\right)$(x−(−h))=(x+h) than we have a horizontal translations of $h$h units left.
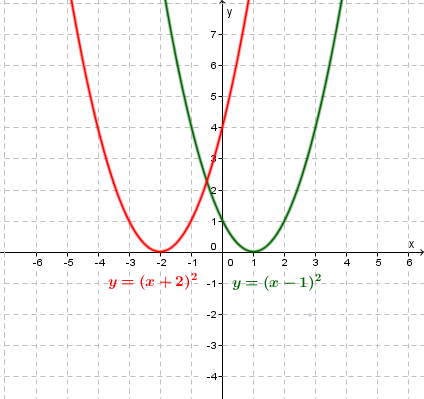
The graph $y=x^2$y=x2 being horizontally translated $2$2 units left
to $y=\left(x+2\right)^2$y=(x+2)2 and $1$1 unit right to $y=\left(x-1\right)^2$y=(x−1)2
Identifying transformations
The form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k shows us:
Vertical Dilation a
If $\left|a\right|>1$|a|>1 then the quadratic is steeper than $x^2$x2.
If $\left|a\right|<1$|a|<1 then the quadratic is flatter than $x^2$x2.
Reflection a
If $a<0$a<0 then the quadratic is a reflection of $ax^2$ax2 on a line parallel to the $x$x-axis.
Vertical Translation k
If $k>0$k>0 then the translation is up.
If $k<0$k<0 then the translation is down.
Horizontal Translation h
If $h<0$h<0 then the translation is to the left, and $x+h$x+h appears in the brackets.
If $h>0$h>0 then the translation is to the right, and $x-h$x−h appears in the brackets.
Examples
Question 10
The function $y=-5x^2$y=−5x2 has what dilation factor?
Dilation factor $=$= $\editable{}$
Question 11
The quadratic $y=x^2$y=x2 has been transformed into $y=3\left(x-4\right)^2$y=3(x−4)2. Has there been a reflection?
Yes, across the $x$x-axis
AYes, across the $y$y-axis
BNo$\text{ }$
C
Question 12
The quadratic $y=x^2$y=x2 has been transformed into $y=-4\left(x+10\right)^2$y=−4(x+10)2. Identify the vertical translation.
$0$0 units up or down
A$4$4 units up
B$10$10 units down
C$10$10 units up
D
Question 13
The quadratic $y=x^2$y=x2 has been transformed into the following graph:
What is the vertical translation?
$4$4 units up
A$4$4 units down
B$3$3 units down
C$3$3 units up
DWhat is the horizontal translation?
$3$3 units right
A$4$4 units left
B$3$3 units left
C$4$4 units right
DHas the curve been reflected about the $x$x-axis?
No
AYes
BHas this quadratic had a change in dilation from the standard $y=x^2$y=x2 curve?
Yes
ANo
B


