Topics
10. Measurement
topic badge
iGCSE (2021 Edition)

10.14 Surface area of cones, pyramids and spheres

Lesson
Worksheet
Practice
Lesson

Pyramids

A pyramid can be made in the following way. Use any polygon as a base. There can be square bases, triangular bases or even hexagonal bases. Then, connect every vertex of the base to an apex point above the base, and you have a pyramid.

Square and rectangular based pyramids, are the most common you will come across in mathematics, but also in the real world.

In the interactive below, notice that the slope height corresponds to the height of the 2D triangle, which is used in calculating surface area.

Created with Geogebra
Adapted from Edward Knote

Surface area of right pyramid

$\text{Surface area of right pyramid }=\text{Area of base }+\text{Area of triangles }$Surface area of right pyramid =Area of base +Area of triangles

Practice question

Question 1

Find the surface area of the square pyramid shown. Include all faces in your calculations.

A pyramid with a square base and four lateral faces is displayed. Each side of the square base is marked with single tick, measured as 4 cm in length. A slant height extending from one side of the base through the lateral face to the apex of the pyramid is measured as 7 cm. The slant height is perpendicular to the side of square base, indicated by a right angle symbol.

 

Spheres

A solid three-dimensional circular object is a sphere.

Archimedes showed that the surface area of the circular component of the cylinder wrapping the circle, has area $2\pi r\times2r=4\pi r^2$2πr×2r=4πr2 and that this area is the same value for the surface area of a sphere.

Surface area of a sphere

$\text{Surface area of a sphere }=4\pi r^2$Surface area of a sphere =4πr2

Practice question

Question 2

Find the surface area of the sphere shown.

Round your answer to two decimal places.

A sphere is depicted with a circle drawn in solid green line. Dashed green lines are also drawn to represent the area of the sphere that are not directly visible and to show that it is a three-dimensional figure. The radius of the sphere measuring 11 cm is drawn with a purple line.

 

Cones

The surface area of a cone is related to cylinders in the same way that a pyramid is related to the prism.

Surface area of right cone

$\text{Surface area of right cone}=\text{Area of base }+\text{Area of sector }$Surface area of right cone=Area of base +Area of sector

$SA=\pi r^2+\pi rs$SA=πr2+πrs

Practice question

Question 3

Find the surface area of the cone shown.

Round your answer to two decimal places.

A cone is shown with its circular base at the bottom and its apex pointing upward. The slant height of the cone is measured as 10 cm. The radius of the circular base is measured as 3 cm, as indicated by the line segment drawn from the center to the circumference of the circular base.

 

Compound solids

Sometimes, the shape is a compound solid (also known as a composite solid) it is made up of a combination of other solids. These are some examples of compound solids.

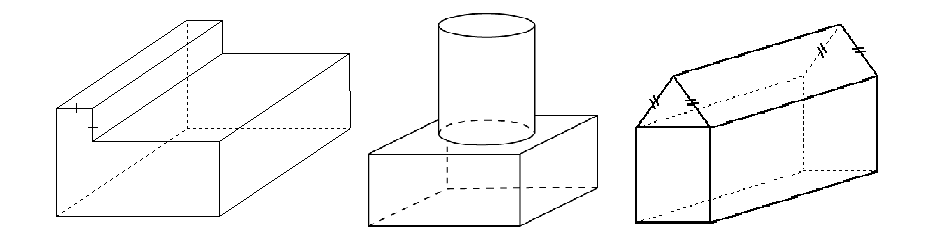
To find the surface area of compound solids, it is necessary to be able to visualise the different shapes that make up the various surfaces. Once these are identified (the different faces and shapes), then calculate the areas of each face and add them up separately.

Don't forget to subtract faces which are not on the surface, like the circle where the cylinder sits on the rectangular prism in the middle image above.

Practice questions

Question 4

In the diagram, the roof has a height of $3$3 metres. Find the surface area of the figure shown,

Round your answer to two decimal places.

A three-dimensional diagram of a composite figure. The structure has a rectangular prism base with dimensions measured 10 m in length, 5 m in width, and a height of 6 m. Attached to the top of the rectangular prism base is a triangular prism, which adds an additional 3 m to the structure’s height. A dashed line indicates the height of the triangle, perpendicular to the base of the triangle. Each of the slanting sides of the triangular base has a single hash mark.

 

Question 5

We wish to find the surface area of the given solid.

  1. What is the surface area of the faces as seen from the top view?

  2. What is the surface area of the faces as seen from the left side view?

  3. What is the surface area of the faces as seen from the front view?

  4. Therefore, what is the total surface area, including all faces of the solid?

Outcomes

0607C7.4B

Surface area of pyramids and cones.

0607C7.4C

Surface area of sphere and hemisphere.

0607E7.4B

Surface area of pyramids and cones.

0607E7.4C

Surface area of sphere and hemisphere.

What is Mathspace

About Mathspace