5.01 Exact values in right-angled triangles

The mnemonic SOHCAHTOA can be useful to help remember the ratios. 

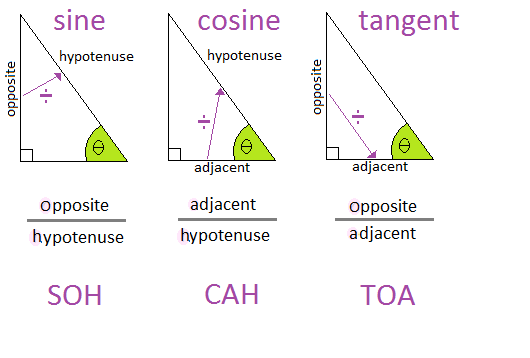
These three trigonometric ratios allow us to find unknown sides and lengths of right-angled triangles. 

 

Exact value triangles

We can create right-angled triangles of varying side lengths and angle combinations. You'll have noticed by now that when you find angles using trigonometric ratios, you often get long decimal answers. If, for example, you put cos(30) into the calculator, you will see an answer of 0.86602... which we'd have to round. However, when you take cos, sin or tan of some angles, you can express the answer as an exact number, rather than a decimal.

There are 2 triangles that are referred to often in trigonometric studies.  These triangles are called exact value triangles, and they look like this:

45 degree angles

Below is a right-angled isosceles triangle, with the equal sides of $1$1 unit. Using Pythagoras' theorem, we can work out that the hypotenuse is $\sqrt{2}$√2 units. Further, because the angles in a triangle add up to $180^\circ$180° and the base angles in an isosceles triangle are equal, we can deduce that the other two unknown angles are both $45^\circ$45°.

Using our trigonometric ratios, we can see that:

• $\sin45^\circ=\frac{1}{\sqrt{2}}$sin45°=1√2​
• $\cos45^\circ=\frac{1}{\sqrt{2}}$cos45°=1√2​
• $\tan45^\circ=\frac{1}{1}$tan45°=11​$=$=$1$1

30 and 60 degree angles

To find the exact ratios of $30$30 and $60$60 degree angles, we need to start with a equilateral triangle with side lengths of $2$2 units. Remember all the angles in an equilateral triangle are $60^\circ$60°.

Then we are going to draw a line that cuts the triangle in half into two congruent triangles. The base line is cut into two $1$1 unit pieces and the length of this centre line was found using Pythagoras' theorem.

Now let's just focus on one half of this triangle.

Using our trigonometric ratios, we can see that:

• $\sin30^\circ=\frac{1}{2}$sin30°=12​
• $\cos30^\circ=\frac{\sqrt{3}}{2}$cos30°=√32​
• $\tan30^\circ=\frac{1}{\sqrt{3}}$tan30°=1√3​
• $\sin60^\circ=\frac{\sqrt{3}}{2}$sin60°=√32​
• $\cos60^\circ=\frac{1}{2}$cos60°=12​
• $\tan60^\circ=\sqrt{3}$tan60°=√3

Exact value summary table

This table is another way to display the information in the exact value triangles. You can choose which method you prefer to help you remember these exact ratios.

	sin	cos	tan
$30^\circ$30°	$\frac{1}{2}$12​	$\frac{\sqrt{3}}{2}$√32​	$\frac{1}{\sqrt{3}}$1√3​
$45^\circ$45°	$\frac{1}{\sqrt{2}}$1√2​	$\frac{1}{\sqrt{2}}$1√2​	$1$1
$60^\circ$60°	$\frac{\sqrt{3}}{2}$√32​	$\frac{1}{2}$12​	$\sqrt{3}$√3

Note that, as mentioned above, the sides of similar right-angled triangles will always be in the same ratio. This allows us to obtain exact rather than rounded values.  One of the best ways to remember them is through the use of the triangle diagrams.

We can also extend the concept of exact values, using Pythagoras' theorem, to determine the trigonometric ratios for any triangle that we are given the length of two sides. See example 5 below.

Worked examples

Example 4

Determine $x$x in the following triangle:

	$\sin30^\circ$sin30°	$=$=	$\frac{x}{4}$x4​
But	$\sin30^\circ$sin30°	$=$=	$\frac{1}{2}$12​	(Exact Value)
Therefore	$\frac{x}{4}$x4​	$=$=	$\frac{1}{2}$12​
Therefore	$x$x	$=$=	$\frac{4}{2}$42​
	$x$x	$=$=	$2$2

Example 5

Given $\sin\theta$sinθ, determine the exact value of $\tan\theta$tanθ

First construct a right-angled triangle with the given information:

Remember	$\tan\theta$tanθ	$=$=	$\frac{O}{A}$OA​
	$\tan\theta$tanθ	$=$=	$\frac{BC}{AC}$BCAC​

The adjacent side $AC$AC can be determined using Pythagoras' theorem as follows:

		$AC^2+1^2=5^2$AC2+12=52
		$AC^2=25-1$AC2=25−1
		$AC=\sqrt{24}$AC=√24
		$AC=2\sqrt{6}$AC=2√6
Therefore		$\tan\theta=\frac{1}{2\sqrt{6}}$tanθ=12√6​