8.03 Surface area of solids
In construction, surface area affects planning (how much to buy) and costs (how much to charge) in connection with such things as wallboard, shingles, and paint.
In manufacturing you will have the same issues - say, the cost of making boxes or printing, or sheet metal parts.
In designing, surface area enters into calculations of wind resistance and drag in cars or airplanes, pressure and strength of materials.
The surface area exposed to air affects how fast something cools, heats or dries out. 
Elephants, for example, need big ears to increase their surface area for cooling purposes, so it's not only human designers that have to do these calculations.
Prisms
A prism has two end faces which are congruent (exactly the same).
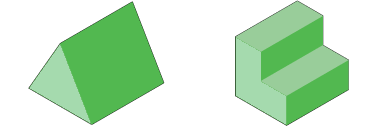
It also has a number of lateral faces that join the 2 end faces together. For example, this triangular prism has 2 triangular end faces and 3 additional lateral faces. We can see that this shape has a net that looks like this:

The surface area of this shape will be the sum of the area of all the faces. The three rectangles have dimensions equal to the lengths of the sides of the triangle and width equal to the lateral length of the prism.
Have a look at this interactive to see how to unfold prisms.
$\text{Surface area of a prism }=\text{Sum of areas of all faces}$Surface area of a prism =Sum of areas of all faces
Practice question
Question 1
The dimensions of a trapezoidal prism are given in the following diagram (not drawn to scale):
Find the surface area of the trapezoidal prism.
Cylinders
A cylinder has two parallel bases that are connected by a curved surface.
Surface area of a cylinder = Area of the 2 circular end faces + Area of curved lateral surface (rectangle)
= $\left(2\times\pi r^2\right)+\left(L\times W\right)$(2×πr2)+(L×W)
Area of each circle: the radius of each circle is the same as the radius of the cylinder
Area of the rectangle: the width of the rectangle corresponds to the height of the prism, while the length of the rectangle is the circumference of the circle ( $2\pi r$2πr )
$\text{Area curved surface of a cylinder }=2\pi rh$Area curved surface of a cylinder =2πrh
$\text{Surface area of a cylinder with one end }=\pi r^2+2\pi rh$Surface area of a cylinder with one end =πr2+2πrh
$\text{Surface area of a cylinder with two ends }=2\pi r^2+2\pi rh$Surface area of a cylinder with two ends =2πr2+2πrh
Practice question
Question 2
Find the surface area of the cylinder shown.
Give your answer to the nearest two decimal places.

Pyramids
A pyramid can be made in the following way: Use any polygon as a base. We can have square bases, triangular bases or even hexagonal bases. Then connect every vertex of the base to an apex point above the base, and you have a pyramid.
If the apex is directly above the centre of the base it is a right pyramid. These are all right pyramids.

We can identify a pyramid by the shape of the base. Square and rectangular based pyramids, are the most common you will come across in mathematics, but also in the real world.



As you can see from these pictures, the triangular shaped sides slope towards the apex. This introduces a new term we use in calculations with pyramids called the Slant Height (or Slope Height).
In the interactive below, look at the triangular faces of the pyramid. You can see that the slope height corresponds to the height of the 2D triangle, which we will use in calculating surface area.
As we found with other 3D shapes, calculating the surface area of a solid is done by adding the area of all faces. For right pyramids, we have the base and a number of triangular faces.
$\text{Surface Area of Right Pyramid }=\text{Area of Base }+\text{Area of triangles }$Surface Area of Right Pyramid =Area of Base +Area of triangles
Practice question
Question 3
Find the surface area of the square pyramid shown. Include all faces in your calculations.

Cones
A cone is made by connecting a circular base to an apex. If the apex is directly perpendicular to the centre of the base, it is called a right cone.
Cone shapes appear everywhere in the real world.


Using the interactive below you can see what happens when we unravel a cone. This will help us to see the shapes we need to work out its surface area.

The area of this large circle with radius $s$s, would be $\pi s^2$πs2
The circumference of the large circle with radius $s$s would be $2\pi s$2πs.
The pink arc AB originally wrapped around the base of the cone, and so its length is the circumference of the base. So the length of arc AB is $2\pi r$2πr
The ratio of the blue shaded sector to the area of the whole circle, is the same as the ratio of the pink arc AB to circumference of the whole circle.
We can write this as an equation.
| $\frac{\text{area of sector }}{\text{area of whole circle }}$area of sector area of whole circle | $=$= | $\frac{\text{length of arc }}{\text{circumference of large circle }}$length of arc circumference of large circle |
| $\frac{\text{area of sector }}{\pi s^2}$area of sector πs2 | $=$= | $\frac{2\pi r}{2\pi s}$2πr2πs |
| $\text{area of sector }$area of sector | $=$= | $\frac{r}{s}\times\pi s^2$rs×πs2 |
| $\text{area of sector }$area of sector | $=$= | $\pi rs$πrs |
$\text{Surface area of a right cone}=\text{Area of base }+\text{Area of sector }$Surface area of a right cone=Area of base +Area of sector
$SA=\pi r^2+\pi rs$SA=πr2+πrs
Where $r$r is the radius and $s$s is the slant height
(note that slant height is named using the variable $l$l in the IB formula booklet).
Practice question
Question 4
Find the surface area of the cone shown.
Round your answer to two decimal places.

Sphere
A solid 3-dimensional circular object is a sphere. Half of a sphere is called a hemisphere.
Unlike solids we have seen so far, we cannot unwrap a sphere, get a 2D net and calculate its area. So the surface area of a sphere is approached in a different way. Archimedes discovered that a cylinder that circumscribes a sphere, as shown in this picture, has a curved surface area equal to the surface area, S, of the sphere.

Archimedes showed that the surface area of the circular component of the cylinder wrapping the circle, has area $2\pi r\times2r=4\pi r^2$2πr×2r=4πr2 and that this area is the same value for the surface area of a sphere.
$\text{Surface area of a sphere }=4\pi r^2$Surface area of a sphere =4πr2
Practice question
Question 5
Find the surface area of the sphere shown.
Round your answer to two decimal places.
Composite solids
Sometimes, the shape is a composite solid, (made up of a combination of other solids). These are all composite solids:
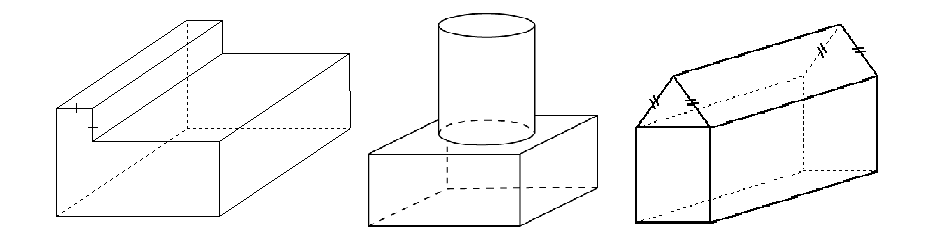
To find the surface area of composite solids we need to be able to visualise the different shapes that make up the various surfaces.
Don't forget to subtract faces which are not on the surface, like the circle where the cylinder sits on the rectangular prism in the middle image above.
Practice questions
Question 6
Find the surface area of the figure shown.

Question 7
Find the surface area of the prism shown.
Round your answer to two decimal places.


