Eulerian and semi-Eulerian graphs
Consider the following graphs. Check that you can start at one vertex and travel along each edge exactly once without lifting your pen from the paper.

Each graph has a trail that uses every edge exactly once. The trail on the left is open and starts and finishes at different vertices. The graph on the right is closed and any vertex can be the start/end.
Traversable is the word to describe graphs where you can start at a vertex and draw in all the edges without taking your pen off the page or retracing any edge. The two types of traversable graphs are:
- If a graph has a closed trail (it starts and finishes at the same vertex) that uses every edge, it is called Eulerian (named after the same Euler who gave us the formula $v+f-e=2$v+f−e=2). It can also be called an Eulerian trail or an Eulerian circuit.
- If a graph has an open trail (it starts and finishes at different vertices) that uses every edge, it is described as semi-Eulerian. It can also be called a semi-Eulerian trail.
It is possible to determine if an undirected graph is Eulerian or semi-Eulerian without having to actually find the trail:
- If a graph has exactly two vertices of odd degree, then the graph is semi-Eulerian. These two vertices will be the start and the end of the open semi-Eulerian trail.
- If a graph has all even vertices, then the graph is Eulerian. The closed Eulerian trail can start at any vertex.
Worked example
Example 1
Describe the network below as Eulerian, semi-Eulerian or neither. Justify your answer.

Think: Calculate the degree of each vertex. Eulerian will have all even vertices, semi-Eulerian will have exactly two odd vertices.
Do: Write - The graph is semi-Eulerian because the top and bottom vertices are both odd (degree 5) and the other two vertices are even (degree 2).
Practice questions
Question 1
Suppose $G$G is a very large network, with $300$300 vertices, each of even degree.
Does a semi-Eulerian trail exist for $G$G?
Select all that apply.
Yes, as there are exactly two vertices of odd degree.
AYes, as there are no vertices with odd degree.
BYes, as there are an even number of even vertices and an even number of odd vertices.
CNo, as there are no vertices with odd degree.
DDoes an Eulerian circuit exist for $G$G? Select all correct answers:
Yes, as there are no vertices with odd degree.
AYes, as there are an even number of even vertices and an even number of odd vertices.
BYes, as there are exactly two vertices of odd degree.
CNo, as there are no vertices with odd degree.
D
Question 2
Consider the following network:

Is it possible to draw an Eulerian circuit (also called Euler circuit) on the following network?
Yes
ANo
BWrite an Eulerian circuit starting with the vertex $B$B.
Enter all the vertices on the same line, separated by a comma, like this: $M,N,O,P,M$M,N,O,P,M
Question 3
Consider the network below:

Is the network Eulerian or semi-Eulerian?
The graph is Eulerian (it can be traversed and starts and ends at the same vertex).
AThe graph is semi-Eulerian (it can be traversed but starts and ends at different vertices).
BThe graph is not Eulerian or semi-Eulerian
CWhich vertex or vertices can the trail start at? Select all correct options:
$A$A
A$B$B
B$C$C
C$D$D
D$E$E
E$F$F
FSarah has started to traverse through the graph, by moving along the vertices $B,C,D$B,C,D. Which vertices are possible to travel to next along such a trail? Select all the correct options.
$A$A
A$B$B
B$C$C
C$D$D
D$E$E
E$F$F
FEnter a semi-Eulerian trail for the network that completes Sarah's journey.
Enter each vertex as a capital letter in order, separated by commas.
Hamiltonian and semi-Hamiltonian graphs
When we looked at Eulerian graphs, we were focused on using each of the edges just once.
We will now look at Hamiltonian graphs, which are named after Sir William Hamilton - an Irish mathematician, physicist and astronomer.
A Hamiltonian graph is a graph which has a closed path (cycle) that visits each vertex exactly once, ending on the same vertex as it began. This closed path is also called a Hamiltonian cycle.
In the graph below, the Hamiltonian cycle is marked in red. As it is a cycle, we cannot have repeated edges or repeated vertices. Note that we do not need to use all the edges in order to visit each vertex once.
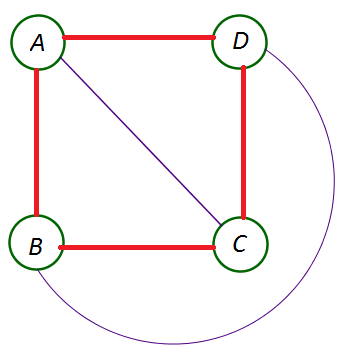
Other Hamiltonian cycles here include $ABDCA$ABDCA, $DBACD$DBACD, and many others.
A semi-Hamiltonian path is a path that visits every vertex once and starts and ends at different vertices. Semi-Hamiltonian graphs are sometimes called traceable.
If a graph has a Hamiltonian cycle then it automatically has a semi-Hamiltonian path (by just dropping off the last vertex in the cycle we create a path - for example, $ABDC$ABDC and $DBAC$DBAC in the graph above).
Unlike Eulerian and semi-Eulerian paths, there is no systematic procedure to help us identify if a semi-Hamiltonian path or Hamiltonian cycle exists. The only thing we can do is look for them.
Here are three networks:
- the first is semi-Hamiltonian and has a semi-Hamiltonian path highlighted;
- the second is Hamiltonian and has a Hamiltonian cycle highlighted;
- the third does not have a Hamiltonian or semi-Hamiltonian path.

Hamiltonian paths in complete graphs
The following graph is a complete graph. Recall that means each vertex is connected to every other vertex. It has many semi-Hamiltonian paths and Hamiltonian cycles. How many can you find?
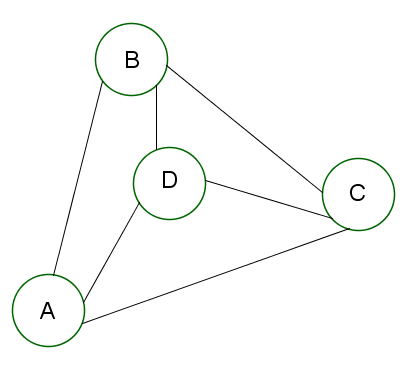
Remember, a semi-Hamiltonian path is a path where we visit each of the vertices only once. Here is the full list of semi-Hamiltonian paths for this graph:
$ABCD$ABCD, $ABDC$ABDC, $ADCB$ADCB, $ADBC$ADBC, $ACBD$ACBD, $ACDB$ACDB, $BACD$BACD, $BADC$BADC, $BCDA$BCDA, $BCAD$BCAD, $BDAC$BDAC, $BDCA$BDCA, $CABD$CABD, $CADB$CADB, $CBDA$CBDA, $CBAD$CBAD, $CDBA$CDBA, $CDAB$CDAB, $DABC$DABC, $DACB$DACB, $DBAC$DBAC, $DBCA$DBCA, $DCAB$DCAB and $DCBA$DCBA.
So the list of semi-Hamiltonian paths is actually just all combinations of the four vertices $A$A, $B$B, $C$C and $D$D.
Also, because it is a complete graph all of the paths listed above can be turned into Hamiltonian cycles by returning to the original node.
In a complete graph with $n$n vertices, each vertex is connected to every other vertex by an edge.
Starting at any vertex there are $n-1$n−1 possible choices of vertices to visit next. After that, there are $n-2$n−2 vertices left to visit, and so on. Since every vertex is connected to every other vertex, this means there are $n!=n\times(n-1)\times(n-2)\times...\times2\times1$n!=n×(n−1)×(n−2)×...×2×1 possible Hamiltonian cycles.
For example, if a complete graph has $4$4 vertices the number of Hamiltonian cycles is given by:
$4!=4\times3\times2\times1=24$4!=4×3×2×1=24
Worked examples
Example 2
State a semi-Hamiltonian path in the graph below. .
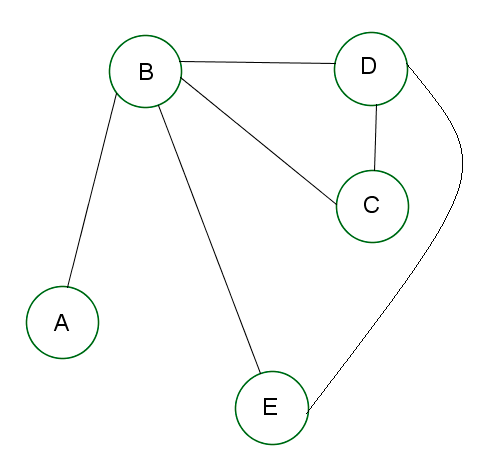
Think: In a semi-Hamiltonian path we need to visit each vertex once but do not need to use all the edges or form a cycle.
Do: The path $ABCDE$ABCDE is semi-Hamiltonian (there are others too!).
Example 3
Determine if this directed network is Hamiltonian, semi-Hamiltonian or neither.
Think: For directed graphs, we can still have Hamiltonian/semi-Hamiltonian paths, to find one use trial and error and make sure you are following the arrows in the correct direction.
Do: This network is semi-Hamiltonian. The paths $PUTSQR$PUTSQR and $QSUTPR$QSUTPR visit each vertex once. It is not possible to create such a path that starts and ends at the same vertex, so the graph is not Hamiltonian.
Practice questions
Question 4
Is it possible to draw a semi-Hamiltonian path on the following diagram?

Yes
ANo
B
Question 5
Which of the following graphs are semi-Hamiltonian?
Select all the correct options.
 A
A B
B C
C D
D
Question 6
A rock band is planning a tour across several cities. The following table represents the routes and distance between the cities at which they will be performing.
| Starting City | Ending City | Distance |
|---|---|---|
| $A$A | $C$C | $9$9 |
| $A$A | $F$F | $6$6 |
| $B$B | $E$E | $11$11 |
| $B$B | $F$F | $5$5 |
| $C$C | $D$D | $3$3 |
| $C$C | $F$F | $7$7 |
| $E$E | $D$D | $5$5 |
| $E$E | $F$F | $8$8 |
Which of the following graphs does the table represent?
 A
A B
B C
C D
DUsing either the correct graph or table given, find the shortest route for the rock band to cross starting at city $A$A and passing by each city only once.
List the vertices in order, separated by commas.
Summary
|
Eulerian (traversable) |
Contains an Eulerian trail - a closed trail (circuit) that includes all edges one time. A graph is Eulerian if all vertices have even degree. |
|
Semi-Eulerian (traversable) |
Contains a semi-Eulerian trail - an open trail that includes all edges one time. A graph is semi-Eulerian if exactly two vertices have odd degree. |
|
Hamiltonian |
Contains a Hamiltonian cycle - a closed path that includes all vertices, other than the start/end vertex, one time. |
|
Semi-Hamiltonian |
Contains a semi-Hamiltonian path - an open path that includes all vertices once. |
A graph can be a traversable Eulerian/semi-Eulerian, a Hamiltonian/semi-Hamiltonian network, both, or neither, as these examples demonstrate:

The first is Eulerian and Hamiltonian, the second is only Hamiltonian, the third is only Eulerian, and the fourth is neither.
