
Banks and other financial institutions allow us to borrow money in the form of a loan, but in return they charge interest on the balance of the loan. While being charged compound interest on the balance of the loan, you also make regular repayments to reduce this balance and eventually repay the loan entirely. So we call these reducing balance loans, and as the amount owing on the loan gets smaller after repayments are made, so does the amount of interest that is charged each period.
Deposit: an initial, partial payment for the cost of the loan.
Balance: the amount owing after interest has been incurred or repayments have been made.
Repayment: a fixed amount paid at regular time periods to repay the balance and any interest incurred.
Interest: an amount charged for loaning you the amount of the balance. Usually calculated as a percentage of the balancing owning using the compound interest formula.
Interest rate: the amount of interest charged expressed as a percentage.
Analysing a reducing balance loan with a table
A table is a useful tool to analyse reducing balance loans. Loan tables can display the progression of the of the loan balance and the interest to be paid in each period. We can also use these figures to calculate the total cost of a loan and the total interest paid.
Exploration
Let's consider the example of using a loan of $\$1000$$1000 at an interest rate of $2.84%$2.84% p.a. compounded annually, that is, interest is charged on the balance of the loan once a year. The loan is for a term of $4$4 years with repayments of $\$268$$268 made at the end of each year.
The interest charged in the first year:
| $\text{Interest}$Interest | $=$= | $0.0284\times\$1000$0.0284×$1000 |
$2.84%$2.84% of the initial loan |
| $=$= | $\$28.40$$28.40 |
|
Balance after $1$1 year:
| $\text{Balance at end of year}$Balance at end of year | $=$= | $\text{Balance at start of year}+\text{Interest}-\text{Payment}$Balance at start of year+Interest−Payment |
| $=$= | $\$1000+\$28.40-\$268$$1000+$28.40−$268 | |
| $=$= | $\$760.40$$760.40 |
This becomes the balance for the start of the second year. And we can continue to find the interest paid for the year by calculating $2.84%$2.84% of the current balance and also the balance at the end of the year using:
$$
The reducing balance for the $4$4 year term of the loan is shown in the table below.
| Year | Balance start of year | Interest added this period | Repayment | Balance end of year |
|---|---|---|---|---|
| $1$1 | $\$1000.00$$1000.00 | $\$28.40$$28.40 | $\$268$$268 | $\$760.40$$760.40 |
| $2$2 | $\$760.40$$760.40 | $\$21.60$$21.60 | $\$268$$268 | $\$514.00$$514.00 |
| $3$3 | $\$514.00$$514.00 | $\$14.60$$14.60 | $\$268$$268 | $\$260.60$$260.60 |
| $4$4 | $\$260.60$$260.60 | $\$7.40$$7.40 | $\$268$$268 | $\$0$$0 |
From the table we can see both the interest to be paid and balance reduce over the term of the loan.
We can calculate the total cost of the loan(total loan amount) using the fact that there were $4$4 equal payments of $\$268$$268.
| $\text{Total loan amount}$Total loan amount | $=$= | $\text{Number of repayments}\times\text{Loan repayment}$Number of repayments×Loan repayment |
| $=$= | $4\times\$268$4×$268 | |
| $=$= | $\$1072$$1072 |
We can calculate the total interest paid by summing the amounts in the interest column of the table or by finding the difference between the total cost of the loan and the initial amount borrowed.
| $\text{Total interest paid}$Total interest paid | $=$= | $\text{Total loan amount}-\text{Initial amount borrowed}$Total loan amount−Initial amount borrowed |
| $=$= | $\$1072-\$1000$$1072−$1000 | |
| $=$= | $\$72$$72 |
Hence, this loan cost a total of $\$1072$$1072, of which $\$72$$72 was interest.
$\text{Total loan amount}=\text{Number of repayments}\times\text{Loan repayment}$Total loan amount=Number of repayments×Loan repayment
$\text{Total interest paid}=\text{Total loan amount}-\text{Initial amount borrowed}$Total interest paid=Total loan amount−Initial amount borrowed
Final payments
In the example above the payments coincided exactly with paying the loan off in $4$4 years. In practice we often round payments to a convenient figure such as rounding a home loan repayment to the nearest $\$10$$10. This leads to the final payment being different from the previous payments. The final adjusted payment is to pay off the remaining balance in the last period plus interest on this amount.
Worked example
Example 1
A small in store loan to is used to purchase a new pair of shoes for $\$300$$300. Interest of $10%$10% per week is charged on the balance of the loan, and we are able to pay back $\$100$$100 each week.
(a) Using the table below, find the final payment due on the loan.
| Period (n) | Value at beginning of period | Interest added this period | Repayment | Value at end of period |
|---|---|---|---|---|
| $1$1 | $\$300$$300 | $\$30$$30 | $\$100$$100 | $\$230$$230 |
| $2$2 | $\$230$$230 | $\$23$$23 | $\$100$$100 | $\$153$$153 |
| $3$3 | $\$153$$153 | $\$15.30$$15.30 | $\$100$$100 | $\$68.30$$68.30 |
| $4$4 | $\$68.30$$68.30 | $\editable{}$ | $\editable{}$ | $\$0$$0 |
Think: The final payment needs to pay off the remaining balance of $\$68.30$$68.30 plus interest on this amount.
Do:
| $\text{Interest}$Interest | $=$= | $\$68.30\times0.1$$68.30×0.1 |
| $=$= | $\$6.83$$6.83 |
| $\text{Final payment}$Final payment | $=$= | $\text{Remaining balance}+\text{Interest}$Remaining balance+Interest |
| $=$= | $\$68.30+\$6.83$$68.30+$6.83 | |
| $=$= | $\$75.13$$75.13 |
(b) Find the total cost of the loan.
Think: There were three full payments of $\$100$$100 plus a final adjusted payment of $\$75.13$$75.13.
Do:
| $\text{Total loan amount}$Total loan amount | $=$= | $\text{Number of full payments}\times\text{Repayment}+\text{Final adjusted payment}$Number of full payments×Repayment+Final adjusted payment |
| $=$= | $3\times\$100+\$75.13$3×$100+$75.13 | |
| $=$= | $\$375.13$$375.13 |
(c) How much interest was paid on the loan?
Think: The interest is the difference between the total cost of the loan and the amount borrowed.
Do:
| $\text{Total interest paid}$Total interest paid | $=$= | $\text{Total loan amount}-\text{Initial amount borrowed}$Total loan amount−Initial amount borrowed |
| $=$= | $\$375.13-\$300$$375.13−$300 | |
| $=$= | $\$75.13$$75.13 |
Practice questions
Question 1
Dylan takes out a loan to purchase a property. He makes equal monthly loan repayments of $\$4600$$4600 over $27$27 years to pay it off. The interest of $8%$8% is compounded annually.
What is the total loan amount?
Question 2
Ivan takes out a car loan for $\$24000$$24000. He is charged $8.1%$8.1% per annum interest, compounded monthly. Ivan makes repayments of $\$450$$450 at the end of each month.
Complete the values in the empty cells in the table below. Give your answers correct to the nearest cent.
Month Opening Balance Interest Repayment Closing Balance 1 $24000$24000 $162.00$162.00 $450$450 $23712.00$23712.00 2 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ 3 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$
Question 3
You take out a personal loan of $\$10000$$10000 at $11%$11% reducible p.a. The term of the loan is $3$3 years, and yearly repayments of $\$2600$$2600 are made. The balance owing is paid at the end of $3$3 years.
Complete the loan repayment table:
Year Balance of loan at beginning of period Interest charged during period Repayment Balance of loan at end of period $1$1 $10000$10000 $\editable{}$ $2600$2600 $\editable{}$ $2$2 $\editable{}$ $\editable{}$ $2600$2600 $\editable{}$ $3$3 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ What is the total amount of interest charged on the loan?
What is the total repayment over $3$3 years?
Using a financial table
Banks offer different repayment plans depending on the amount you borrow, the interest rate you pay, and the length of your loan. To calculate the payments required to pay off a loan at a given rate and term we can use online financial calculators, the financial application found in many calculators or financial tables of estimated payments for standard loans.
Worked example
Example 2
The table below gives the monthly repayment of a $\$1000$$1000 loan at different rates and terms.
| Monthly repayments on a $\$1000$$1000 loan | |||||
|---|---|---|---|---|---|
| Term of loan in years | |||||
| Annual interest rate | $10$10 | $15$15 | $20$20 | $25$25 | $30$30 |
| $3%$3% | $9.66$9.66 | $6.91$6.91 | $5.55$5.55 | $4.74$4.74 | $4.22$4.22 |
| $4%$4% | $10.12$10.12 | $7.40$7.40 | $6.06$6.06 | $5.28$5.28 | $4.77$4.77 |
| $5%$5% | $10.61$10.61 | $7.91$7.91 | $6.60$6.60 | $5.85$5.85 | $5.37$5.37 |
| $6%$6% | $11.10$11.10 | $8.44$8.44 | $7.16$7.16 | $6.44$6.44 | $6.00$6.00 |
| $7%$7% | $11.61$11.61 | $8.99$8.99 | $7.75$7.75 | $7.07$7.07 | $6.65$6.65 |
| $8%$8% | $12.13$12.13 | $9.56$9.56 | $8.36$8.36 | $7.72$7.72 | $7.34$7.34 |
(a) Use the table to estimate the monthly repayments on a $\$150000$$150000 loan for a term of $20$20 years at $6%$6% p.a..
Think: If we borrowed $\$15000$$15000, we would be borrowing $15$15 lots of $\$1000$$1000. Looking in the table across the $6%$6% row we see that the repayments would be approximately $\$7.16$$7.16 per $\$1000$$1000.
Do:
| $\text{Monthly repayment}$Monthly repayment | $=$= | $\$7.16\times15$$7.16×15 |
| $=$= | $\$107.40$$107.40 |
(b) What is the estimated total interest paid on the loan in part (a)?
Think: We have monthly payments for $20$20 years, so there will be a total of $20\times12=240$20×12=240 payments. And the interest paid is the difference between the total cost of the loan and the initial amount borrowed.
Do:
| $\text{Total loan amount}$Total loan amount | $=$= | $\text{Number of repayments}\times\text{Loan repayment}$Number of repayments×Loan repayment |
| $=$= | $240\times\$107.40$240×$107.40 | |
| $=$= | $\$25776$$25776 |
| $\text{Total interest paid}$Total interest paid | $=$= | $\text{Total loan amount}-\text{Initial amount borrowed}$Total loan amount−Initial amount borrowed |
| $=$= | $\$25776-\$15000$$25776−$15000 | |
| $=$= | $\$10776$$10776 |
So we'd actually end up paying $\$10776$$10776 interest over the $20$20 years. This is a considerable amount of interest, due in part to the long term of the loan.
Practice question
Question 4
Using the financial table, calculate the monthly instalments required to pay off a $25$25-year loan of $\$1000$$1000 at $4%$4% p.a. monthly reducible interest.
| Term of Loan in years | |||||
|---|---|---|---|---|---|
| Annual interest rate | $10$10 | $15$15 | $20$20 | $25$25 | $30$30 |
| $3%$3% | $9.66$9.66 | $6.91$6.91 | $5.55$5.55 | $4.74$4.74 | $4.22$4.22 |
| $4%$4% | $10.12$10.12 | $7.40$7.40 | $6.06$6.06 | $5.28$5.28 | $4.77$4.77 |
| $5%$5% | $10.61$10.61 | $7.91$7.91 | $6.60$6.60 | $5.85$5.85 | $5.37$5.37 |
| $6%$6% | $11.10$11.10 | $8.44$8.44 | $7.16$7.16 | $6.44$6.44 | $6.00$6.00 |
| $7%$7% | $11.61$11.61 | $8.99$8.99 | $7.75$7.75 | $7.07$7.07 | $6.65$6.65 |
| $8%$8% | $12.13$12.13 | $9.56$9.56 | $8.36$8.36 | $7.72$7.72 | $7.34$7.34 |
| Term of Loan in years | |||||
| Annual interest rate | $10$10 | $15$15 | $20$20 | $25$25 | $30$30 |
| $3%$3% | $9.66$9.66 | $6.91$6.91 | $5.55$5.55 | $4.74$4.74 | $4.22$4.22 |
| $4%$4% | $10.12$10.12 | $7.40$7.40 | $6.06$6.06 | $5.28$5.28 | $4.77$4.77 |
| $5%$5% | $10.61$10.61 | $7.91$7.91 | $6.60$6.60 | $5.85$5.85 | $5.37$5.37 |
| $6%$6% | $11.10$11.10 | $8.44$8.44 | $7.16$7.16 | $6.44$6.44 | $6.00$6.00 |
| $7%$7% | $11.61$11.61 | $8.99$8.99 | $7.75$7.75 | $7.07$7.07 | $6.65$6.65 |
| $8%$8% | $12.13$12.13 | $9.56$9.56 | $8.36$8.36 | $7.72$7.72 | $7.34$7.34 |
Analysing loans using spreadsheets
It is common to use tables to view the progression of a loan. The investigations in this chapter explore how to set up spreadsheets and a further look at analysing loans in particular, using spreadsheets to automate calculating the values. This can be particularly useful when there are frequent compounds and/or a loan with a long term. Using a spreadsheet we can quickly explore the impact of changes such as interest rates, compounding periods, or making higher regular payments.
Worked example
Example 3
Mr and Mrs Roberts take out a mortgage to purchase a house. They borrow $\$550000$$550000 from a bank that charges them $5.8%$5.8% interest per annum, compounded monthly. At the end of each month the Roberts make a repayment of $\$3500$$3500.
The first and last months of the loan are shown in the spreadsheet below.
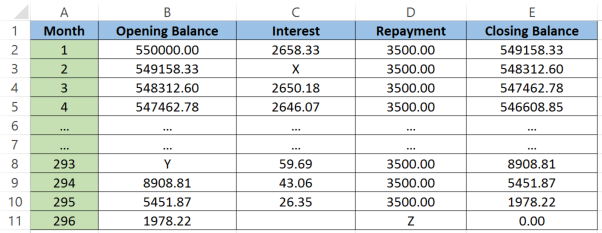
Note the calculations used to create this spreadsheet
- In cell B2, opening balance = closing balance for previous month
- In cell C1, monthly interest = annual rate/12 * opening balance
- In cell D2, repayment = fixed amount (except for last month)
- In cell E2, closing balance = opening balance + interest - repayment
(a) Calculate the value of X in the table.
Think: X is situated in the interest column, so we need to find the interest on the amount at the start of month $2$2. We must first divide the interest rate by $12$12 as interest is calculated monthly.
Do:
| $X$X | $=$= | $\frac{0.058}{12}\times549158.33$0.05812×549158.33 |
Rate multiplied by balance at start of month. |
| $=$= | $2654.27$2654.27 |
Round to 2 decimal places. |
(b) Calculate the value of Y in the table.
Think: Usually finding the opening balance is easy because it's the same as the closing balance from the previous time period. But we can't see it in this case. So we'll need to work backwards by writing an equation and solving it.
Do: Using the equation for the closing balance we have:
| $\text{Opening balance}+\text{Interest}-\text{Payment}$Opening balance+Interest−Payment | $=$= | $\text{Closing balance}$Closing balance | |
| $Y+56.59-3500$Y+56.59−3500 | $=$= | $8908.81$8908.81 |
Rearrange to isolate $Y$Y. |
| $=$= | $8908.81-56.59+3500$8908.81−56.59+3500 |
|
|
| $=$= | $12349.12$12349.12 |
|
(c) Calculate the value of Z in the table.
Think: This is the month where the Roberts will crack open a bottle of champagne since they've finally paid off their loan! Their final repayment will be less than their usual amount. It will be equal to the amount owing at the end of the second last month plus the interest on the amount owing.
Do:
| $\text{Final payment}$Final payment | $=$= | $\text{Remaining balance}+\text{Interest}$Remaining balance+Interest |
| $Z$Z | $=$= | $1978.22+\frac{0.058}{12}\times1978.22$1978.22+0.05812×1978.22 |
| $=$= | $1987.78$1987.78 |
(d) Calculate the total repayments made by the Roberts.
Think: The Roberts have made $295$295 repayments each of $\$3500$$3500 plus the final repayment of $\$1987.78$$1987.78
Do:
| $\text{Total repayments}$Total repayments | $=$= | $\text{Number of full payments}\times\text{Repayment}+\text{Final adjusted payment}$Number of full payments×Repayment+Final adjusted payment |
| $=$= | $295\times\$3500+\$1987.78$295×$3500+$1987.78 | |
| $=$= | $\$1034487.78$$1034487.78 |
(e) Hence determine the total interest the Roberts paid for the loan.
Think: The total interest paid on the loan is their total repayments minus the amount they borrowed.
Do:
| $\text{Total interest paid}$Total interest paid | $=$= | $\text{Total repayments}-\text{Initial amount borrowed}$Total repayments−Initial amount borrowed |
| $=$= | $\$1034487.78-\$550000$$1034487.78−$550000 | |
| $=$= | $\$484487.78$$484487.78 |
So we can see that they nearly paid double the purchase price over the $296$296 months, or $25$25 years.
Reflect: How could they pay off their house sooner?
They could try to do one or both of the following:
-
Halve the monthly payment and make this new payment fortnightly. This saves a significant amount as they will effectively be making an extra month's payment per year and will pay the loan off sooner. They would end up making an extra repayment each year since there are $26$26 fortnights in a year and $\frac{26}{2}=13$262=13 so they would have paid for $13$13 months instead of $12$12.
-
Increase the amount they repay. Intuitively, if you make larger repayments each month or fortnight, you'll be able to pay off your loan sooner, saving you a lot of interest and thus helping you pay less overall.
Practice question
Question 5
Mr. and Mrs. Dave have a mortgage.
The final months of their repayments are shown below.
Month Opening Balance Interest Repayment Closing Balance $146$146 $26452.84$26452.84 $198.40$198.40 $5000$5000 $21651.24$21651.24 $147$147 $21651.24$21651.24 $162.38$162.38 $5000$5000 $16813.62$16813.62 $148$148 $16813.62$16813.62 $126.10$126.10 $5000$5000 $11939.72$11939.72 $149$149 $11939.72$11939.72 $89.55$89.55 $5000$5000 $7029.27$7029.27 $150$150 $7029.27$7029.27 $52.72$52.72 $5000$5000 $2081.99$2081.99 Calculate the monthly interest rate charged on this loan. Give your answer as an percentage to two decimal places.
Complete the next row of the table, giving your answers correct to two decimal places.
Month Opening Balance Interest Repayment Closing Balance $146$146 $26452.84$26452.84 $198.40$198.40 $5000$5000 $21651.24$21651.24 $147$147 $21651.24$21651.24 $162.38$162.38 $5000$5000 $16813.62$16813.62 $148$148 $16813.62$16813.62 $126.10$126.10 $5000$5000 $11939.72$11939.72 $149$149 $11939.72$11939.72 $89.55$89.55 $5000$5000 $7029.27$7029.27 $150$150 $7029.27$7029.27 $52.72$52.72 $5000$5000 $2081.99$2081.99 $151$151 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ How many years did it take for them to pay off the loan?
Give your answer in the form of a mixed number.
Calculate the total repayments.
If they paid $\$302097.60$$302097.60 in interest, how much did they initially borrow?