In our last lesson we described the strength of the correlation between two variables as either weak, moderate or strong. However, the perceived strength of the correlation may depend on the scale of the scatter plot, the size of the data points or simply the observers opinion. To objectively measure the strength of a relationship we can use one of many statistical tests and measurements. A common tool for determining the strength of a correlation is Pearson's correlation coefficient. For this lesson we will focus on interpreting the value of the correlation coefficient and will look at how to calculate this using technology in a later lesson.
Pearson's correlation coefficient
Pearson's correlation coefficient is a value that tells you the strength of the linear relationship between two variables. It is denoted by the letter $r$r. It indicates how closely a scatterplot conforms to a straight line.
The value of $r$r ranges from $-1$−1 to $1$1 on a continuum like this.
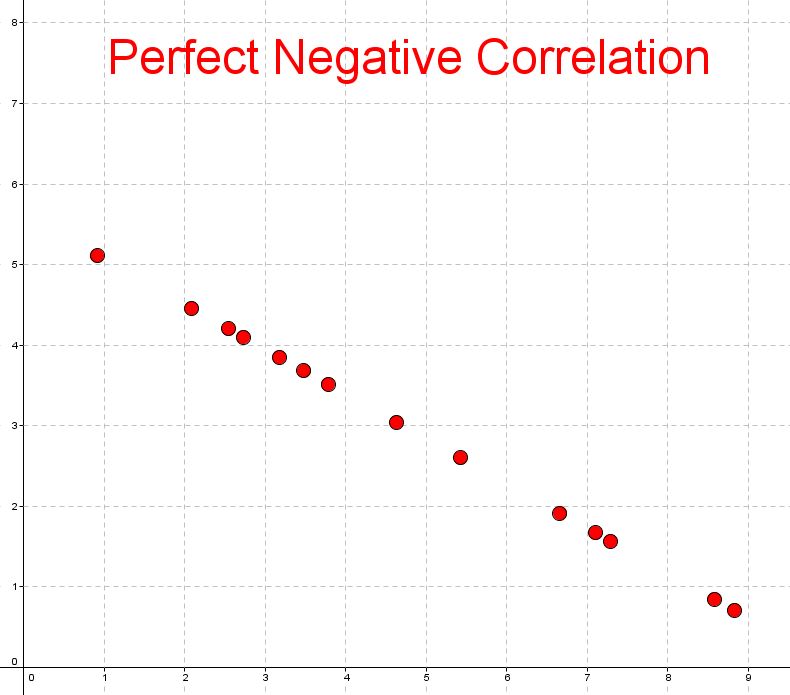
If the $r$r value is $0$0, we say there is no correlation. If the $r$r value is $1$1 or $-1$−1 we say the correlation is perfect.
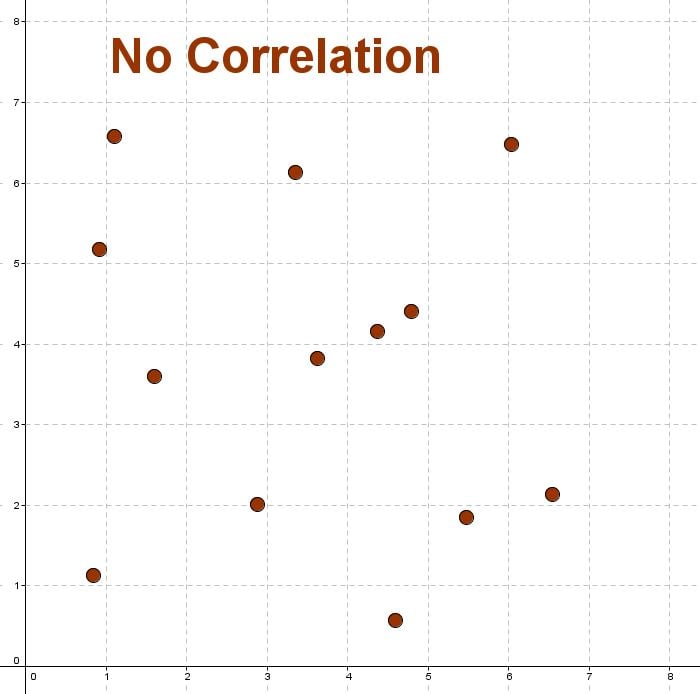
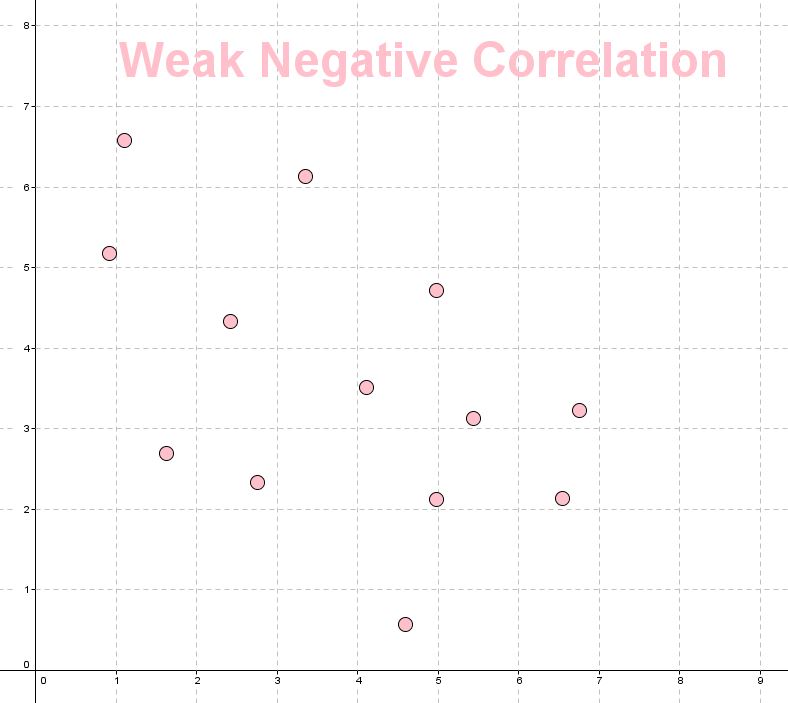
Correlation can be described as perfect, weak, moderate or strong (positive or negative).
Positive correlations
 |
 |
 |
Negative correlations
 |
 |
 |
We can use Pearson's correlation coefficient to describe the strength of a correlation as follows:
- A weak correlation, indicates there is some correlation but it is not considered to be very significant. Values from $0$0 to $0.5$0.5 or from $-0.5$−0.5 to $0$0 are generally considered weak.
- A strong correlation indicates that the connection between the variables is quite significant. Values from approximately $0.8$0.8 to $1$1 or from $-1$−1 to $-0.8$−0.8 are strong.
- A moderate correlation falls between weak or strong. Values from approximately $0.5$0.5 to $0.8$0.8 or from $-0.8$−0.8 to $-0.5$−0.5 are considered moderate.
Correlation applet
Play with this applet to see how the correlation coefficient changes. Move each point. Try having one outlier and see how much that can change the correlation coefficient. Try moving the points so they are in a perfect straight line. What happens to the correlation coefficient value?
|
|
1. State the direction of the relationship. Use the words positive or negative (think about the gradient of the line).
2. Describe the strength of the relationship. Use the $r$r value to determine if the relationship is perfect, weak, moderate, strong or no correlation.
3. State the shape of the relationship. Pearson's correlation coefficient gives a measure of how close the points are to being a straight line, so we almost always use the word linear. It is possible for two variables to be related in a non-linear way. For example, the scatterplot may resemble a parabola more than it resembles a line. If there seems to be a pattern but it does not look like a line we say the relationship appears to be non-linear.
Practice questions
Question 1
Consider the relationship between the variables in the scatterplot below.
Describe the relationship.
No linear relationship
AWeak positive linear relationship
BStrong positive linear relationship
CStrong negative linear relationship
DWeak negative linear relationship
EWhich values could the correlation coefficient take?
Between $-0.2$−0.2 and $0.2$0.2
ABetween $-0.6$−0.6 and $-0.4$−0.4
BBetween $0.8$0.8 and $1$1
CBetween $0.4$0.4 and $0.6$0.6
DBetween $-1$−1 and $-0.8$−0.8
E
Question 2
Describe the relationship between variables with a correlation coefficient of $-0.34$−0.34.
No linear relationship
AStrong negative linear relationship
BWeak positive linear relationship
CStrong positive linear relationship
DWeak negative linear relationship
E
Question 3
In a study, it was found that the correlation coefficient between heights of women and probability of being turned down for a promotion was found to be $-0.90$−0.90.
Which is the most appropriate statement?
There is no evidence of a linear relationship between heights of women and probability of being turned down for a promotion.
AAs the heights of women increases the probability of being turned down for a promotion increases.
BAs the heights of women increases the probability of being turned down for a promotion decreases.
C
Correlation versus causation
A strong correlation might seem to indicate a cause and effect relationships between the variables. However, we need to be very careful to understand the situation at hand, as this is not always the case.
Even when two variables have a strong relationship and $r$r is close to $1$1 or $-1$−1, we cannot say that one variable causes change in the other variable. If asked to asses "does change in the explanatory variable cause change in response variable?" based solely on a strong correlation we can respond "No - correlation does not imply causation".
For example, it has been shown that there is a strong, positive, linear relationship between sunglasses sold and ice-cream cone sales. But we cannot say that sunglasses sales cause ice-cream cone sales. There is a third variable at work here; increase in temperature causes both variables to also increase. Increase in temperature is called a confounding variable.
Common reasons for correlation between variables without a causal relationship:
- Confounding due to a common response to another variable (also described as contributing variables).
- e.g. sales of soup and heaters have a strong positive correlation because they both increase in response to cold winter weather.
- Coincidence - it is possible that the data we are analysing shows a correlation purely by chance.
- e.g. per capita consumption of cheese and deaths from being strangled by a bedsheet have been shown to have a strong correlation. But we cannot say that one causes the other!
- The causation is in the opposite direction
- e.g. strong winds are correlated to tree branches waving. But the waving branches don't cause the strong winds.
- The two variable may interplay, that is the causation may go in both directions
- e.g. There is a negative correlation between number of hawks in an area and rodents in the area. In this type of predator/prey relationship the predator numbers affect prey numbers, but prey numbers, i.e. food supply, also affect predator numbers.
To conclude a causal relationship between variables with a strong correlation confounding factors must be eliminated and a causal mechanism found - such as a carcinogenic ingredients of cigarettes providing a causal link to cancer.
Practice question
Question 4
Which one of the following statements shows a relationship that is correlated but not causal?
The sales of ice cream and increase in temperature.
AThe number of hours worked and how much money is made for a given person.
BThe amount of showers had in a day and the amount of the water bill.
CThe amount of rainfall received, and level of water in a lake.
D
Question 5
A study found a strong correlation between the approximate number of pirates out at sea and the average world temperature.
Does this mean that the number of pirates out at sea has an impact on world temperature?
Yes
ANo
BWhich of the following is the most likely explanation for the strong correlation?
Contributing variables - there are other causal relationships and variables that come in to play and these may lead to an indirect positive association between the approximate number of pirates out at sea and the average world temperature.
ACoincidence - there are no other contributing factors or reasonable arguments to be made for the strong positive association between the approximate number of pirates out at sea and the average world temperature.
BWhich of the following is demonstrated by the strong correlation between the approximate number of pirates out at sea and the average world temperature?
If there is correlation between two variables, then there must be causation.
AIf there is correlation between two variables, there isn't necessarily causation.
BIf there is correlation between two variables, then there is no causation.
C

