2.03 Area

Area of a rectangle

A rectangle is a shape with the specific geometric properties:

• opposite sides equal in length
• opposite sides parallel
• sides meet at right angles.

The area of a rectangle is the size of the space within its boundary. This is the number of unit squares it takes to cover the shape. For a rectangle with length $5$5 centimetres and width $3$3 centimetres, how many squares of size $1$1 cm² would it take to cover it?

If we divide the shape into a grid of $1$1 cm², we can quickly see that it would take $3$3 rows of $5$5 squares to cover the shape, and so the area is $15$15 cm². We can always take this approach of dividing a rectangle into a grid - and in doing so, we obtain the formula for the area of a rectangle:

 

Area of a square

A square is a special kind of rectangle, because it meets all the requirements of a rectangle but has the extra property that all sides are equal length.

To find the area of a square, we use the rectangle rule,

$A=L\times W$A=L×W

Consider this example of a square with sides equal to 4 units:

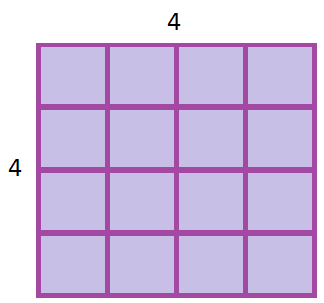		Area	$=$=	$4\times4$4×4
			$=$=	$16$16 square units

 

As the length and width are the same, the area of a square has a simpler rule that we can use:

 

Practice questions

Question 1

Question 2

 

Area of triangles

The area of a triangle is given by the formula $Area=\frac{1}{2}\text{base}\times\text{height}$Area=12​base×height, which can be abbreviated to $A=\frac{1}{2}bh$A=12​bh.

The height in this formula is referring to the height that is perpendicular to the base length. This may be one of the sides of the triangle (like in the right-angled triangle shown above), it may be within the triangle (like the second triangle above), or it may be outside of the triangle (like in the third triangle above).

Where does this formula come from? Notice we can draw a rectangle around any triangle. For example:

In each case, that the area of the triangle is exactly equal to the area of the extra triangles we added to make the each rectangle! So the area of a triangle is half the area of the rectangle with the same base and height.

Use the following applet to see a range of triangles and their related rectangles by moving the points and slider.

Created with Geogebra

 

Worked example

Example 1

Find the area of the triangle pictured below.

Think: Identify the base and perpendicular height and use the formula. Here the base is $7$7 cm and the height perpendicular to this is $8$8 cm.

Do:

 

$A$A	$=$=	$\frac{1}{2}bh$12​bh	Write the formula.
	$=$=	$\frac{1}{2}\times7\times8$12​×7×8 cm2	Substitute in known values and write down units.
	$=$=	$\frac{1}{2}\times56$12​×56 cm2
	$=$=	$28$28 cm2

 

So the area of this triangle is $28$28 cm².

 

 

 

Practice question

Question 3

 

Area of a parallelogram

A parallelogram is a shape with the geometric properties:

• opposite sides equal in length
• opposite sides parallel

 

Parallelogram exploration

Use the applet below to explore how a parallelogram can be broken up and turned into a rectangle.

We know that the area of a rectangle is given by $A=L\times W$A=L×W, so we can work out the area of any parallelogram.

We call the bottom side of the parallelogram the base, and we also need the height of the parallelogram. The height must be measured perpendicularly (at right angles) to the base, not along the sloping side, just like for the area of a triangle.

 

The calculation above is exactly the same as the area of a rectangle even though the rule uses different words for the length and width).

 

Worked example

Example 2

Find the area of the parallelogram shown:

Think: Identify the values for the base and height, then multiply.

Do:

$A$A	$=$=	$b\times h$b×h
	$=$=	$32\times14$32×14 mm2
	$=$=	$30\times14+2\times14$30×14+2×14 mm2
	$=$=	$420+28$420+28 mm2
	$=$=	$48$48 mm2

 

Practice questions

Question 4

 

Area of a trapezium

A trapezium (sometimes called trapezoid) is a shape with:

• One pair of opposite sides that are parallel

 

All of these are trapeziums:

 

Trapezium exploration

The interactive below shows that two identical trapeziums can be joined to form a parallelogram. We can use this property to determine the area of a trapezium.

 

We can see in the diagrams below that two identical trapeziums make a parallelogram with an area:

$\text{Area }=\left(a+b\right)\times h$Area =(a+b)×h.

So a single trapezium must have half of the area of the parallelogram:

$\text{Area }=\frac{1}{2}\times\left(a+b\right)\times h$Area =12​×(a+b)×h

$\text{Area }=\frac{1}{2}\times\left(a+b\right)\times\text{height }$Area =12​×(a+b)×height

$\text{Area }$Area $=$= $\text{base }\times\text{height }$base ×height   $=$= $\left(a+b\right)\times\text{height }$(a+b)×height

 

 

Practice questions

Question 5

Question 6

 

Areas of kites and rhombuses

A kite is a shape with geometric properties:

• Two pairs of adjacent sides that are equal
• One pair of equal angles

Of course the kite you fly around on a windy day is named after the geometric shape it looks like.

A rhombus is a kite with the additional property that all sides are the same length. (A rhombus also meets all the conditions for a parallelogram.)

 

Kite exploration

The interactive below shows that a kite can be broken into triangles, which can be used to determine the area.

 

 

Practice questions

Question 7

Question 8

 

Area of a circle

We already know that area is the space inside a two dimensional shape. We can find the area of a circle, but we will need a special rule.

The following investigation will demonstrate what happens when we unravel sectors of a circle.

When we realign the segments we end up with a parallelogram shape. We can use this to find the area of a circle based on our knowledge that the area of a parallelogram has formula $A=bh$A=bh. The parallelogram formed from a circle has a base length equal to half the circumference and the height is the radius.

 

 

Area of a sector

As we saw in our previous lesson, a sector is a fraction of a circle and the arc length is a fraction of the circumference. The same is true for area: the area of a sector is a fraction of the total area. For example, the area of a semicircle is half the area of the full circle.

Semicircle

$\text{Area of semicircle}=\frac{1}{2}\times\pi r^2$Area of semicircle=12​×πr2

 

We can make a formula for the area of any sector depending on the angle  $\theta$θ that subtends the arc at the centre.

 

 

Practice questions

Question 9

Question 10

QUESTION 11