A sequence in which each term changes from the last by adding a constant amount is called an arithmetic sequence. We refer to the constant the terms are changing by as the common difference, which will result from subtracting any two successive terms $\left(t_{n+1}-t_n\right)$(tn+1−tn).
The progression $-3,5,13,21,\ldots$−3,5,13,21,… is an arithmetic progression with a common difference of $8$8. On the other hand, the progression $1,10,100,1000,\ldots$1,10,100,1000,… is not arithmetic because the difference between each term is not constant.
We denote the first term by the letter $t_1$t1 and the common difference by the letter $d$d. Since, $t_2=t_1+d$t2=t1+d, $t_3=t_2+d$t3=t2+d and so on, we can write any arithmetic sequence as the recurrence relation:
$t_{n+1}=t_n+d$tn+1=tn+d
We can also find an explicit formula in terms of $t_1$t1 and $d$d, this is useful for finding the $n$nth term without listing the sequence.
Let's look at a table of a concrete example to see the pattern for the explicit formula. For the sequence $-3,5,13,21,\ldots$−3,5,13,21,…, we have starting term of $-3$−3 and a common difference of $8$8, that is $t_1=-3$t1=−3 and $d=8$d=8. A table of the sequence is show below:
| $n$n | $t_n$tn | Pattern |
|---|---|---|
| $1$1 | $-3$−3 | $-3$−3 |
| $2$2 | $5$5 | $-3+8$−3+8 |
| $3$3 | $13$13 | $-3+2\times8$−3+2×8 |
| $4$4 | $21$21 | $-3+3\times8$−3+3×8 |
| ... | ||
| $n$n | $t_n$tn | $-3+(n-1)\times8$−3+(n−1)×8 |
The pattern starts to become clear and we could guess that the tenth term becomes $t_{10}=69=-3+9\times8$t10=69=−3+9×8 and the one-hundredth term $t_{100}=789=-3+99\times8$t100=789=−3+99×8. And following the pattern, the explicit formula for the $n$nth term is $t_n=-3+(n-1)\times8$tn=−3+(n−1)×8.
We could create a similar table for the arithmetic progression with starting value $t_1$t1 and common difference $d$d and we would observe the same pattern. Hence, the generating rule for any arithmetic sequence is given by:
$t_n=t_1+\left(n-1\right)d$tn=t1+(n−1)d
For any arithmetic sequence with starting value $t_1$t1 and common difference $d$d, we can express it in either of the following two forms:
- Recursive form is a way to express any term in relation to the previous term:
$t_{n+1}=t_n+d$tn+1=tn+d
- Explicit form is a way to express any term in relation to the term number:
$t_n=t_1+\left(n-1\right)d$tn=t1+(n−1)d
Worked example
Example 1
For the sequence $87,80,73,66...$87,80,73,66..., find and explicit rule for the $n$nth term and hence, find the $30$30th term.
Think: Check that the sequence is arithmetic, does each term differ from the last by a constant? Then write down the the starting value $t_1$t1 and common difference $d$d and substitute these into the general form: $t_n=t_1+(n-1)d$tn=t1+(n−1)d
Do: Each term is a decrease from the last by $7$7. So we have an arithmetic sequence with: $t_1=87$t1=87 and $d=-7$d=−7. The general formula for this sequence is: $t_n=87+\left(n-1\right)\times\left(-7\right)$tn=87+(n−1)×(−7) or $t_n=87-7(n-1)$tn=87−7(n−1).
Hence, the $30$30th term is: $t_{30}=87-7\times29=-116$t30=87−7×29=−116.
Example 2
For the sequence $10,14,18,22,26,...$10,14,18,22,26,..., find $n$n if the $n$nth term is $186$186.
Think: Find a general rule for the sequence, substitute in $186$186 for $t_n$tn and rearrange for $n$n.
Do: This is an arithmetic sequence with $t_1=10$t1=10 and common difference $d=4$d=4. Hence, the general rule is: $t_n=10+\left(n-1\right)\times4$tn=10+(n−1)×4, we can simplify this to $t_n=6+4n$tn=6+4n, by expanding brackets and collecting like terms. Substituting $t_n=186$tn=186, we get:
| $186$186 | $=$= | $6+4n$6+4n |
| $\therefore4n$∴4n | $=$= | $180$180 |
| $n$n | $=$= | $45$45 |
Hence, the $45$45th term in the sequence is $186$186.
Example 3
If an arithmetic sequence has $t_5=38$t5=38 and $t_9=66$t9=66, find the recurrence relation for the sequence.
Think: To find the recurrence relation we need the starting value and common difference. As we have two terms we can set up two equations in terms of $t_1$t1 and $d$d using $t_n=t_1+(n-1)d$tn=t1+(n−1)d.
Do:
| $t_5$t5: | $t_1+4d=38$t1+4d=38 | $.....\left(1\right)$.....(1) |
and
| $t_9$t9: | $t_1+8d=66$t1+8d=66 | $.....\left(2\right)$.....(2) |
If we now subtract equation $\left(1\right)$(1) from equation $\left(2\right)$(2) the first term in each equation will cancel out to leave us with:
| $\left(8d-4d\right)$(8d−4d) | $=$= | $66-38$66−38 |
| $4d$4d | $=$= | $28$28 |
| $\therefore d$∴d | $=$= | $7$7 |
With the common difference found to be $7$7, then we know that, using equation $\left(1\right)$(1) $t_1+4\times7=38$t1+4×7=38 and so $t_1$t1 is $10$10. The recurrence relation for this sequence is given by:
$t_{n+1}=t_n+7$tn+1=tn+7
Practice questions
QUESTION 1
The $n$nth term in an arithmetic progression is given by the formula $T_n=19+5\left(n-1\right)$Tn=19+5(n−1).
Determine $T_1$T1, the first term in the arithmetic progression.
Determine $d$d, the common difference.
Determine $T_9$T9, the $9$9th term in the sequence.
QUESTION 2
The first term of an arithmetic sequence is $5$5. The fifth term is $17$17.
Solve for $d$d, the common difference of the sequence.
Write a recursive rule for $T_{n+1}$Tn+1 in terms of $T_n$Tn which defines this sequence and an initial condition for $T_1$T1.
Write both parts on the same line separated by a comma.
QUESTION 3
In an arithmetic progression where $T_1$T1 is the first term, and $d$d is the common difference, $T_5=18$T5=18 and $T_{10}=33$T10=33.
Determine $d$d, the common difference.
Determine $T_1$T1, the first term in the sequence.
State the equation for $T_n$Tn, the $n$nth term in the sequence.
Hence find $T_{29}$T29, the $29$29th term in the sequence.
Arithmetic sequences in tables and graphs
For any arithmetic sequence in the general form given by $t_n=t_1+\left(n-1\right)d$tn=t1+(n−1)d, we can expand the bracket and collect like terms, creating a new generating rule of the form $t_n=dn+k$tn=dn+k where $d$d and $k$k are constants. For example, the rule $t_n=5+\left(n-1\right)\times2$tn=5+(n−1)×2 is equivalent to $t_n=2n+3$tn=2n+3. This is in the form of the equation of a straight line $\left(y=mx+c\right)$(y=mx+c), so if an arithmetic sequence is plotted as a series of points, they will all lie on a straight line with the gradient being the common difference. This makes sense since we have a constant rate of change.
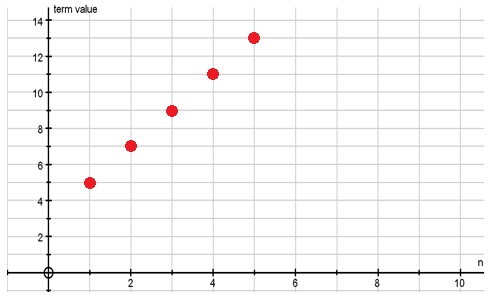
The first term is represented by the point shown at $n=1$n=1, $t_1=5$t1=5 and we can see the gradient here is the common difference $d=2$d=2.
We could also be expected to recognise an arithmetic sequence from a table, such as:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| tn | 5 | 7 | 9 | 11 | 13 |
Here, we can read off the initial term $t_1=5$t1=5 and the common difference can be seen in step between the $t_n$tn values in the second row.
Practice questions
QUESTION 4
The $n$nth term of an arithmetic progression is given by the equation $T_n=12+4\left(n-1\right)$Tn=12+4(n−1).
Complete the table of values.
$n$n $1$1 $2$2 $3$3 $4$4 $10$10 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ By how much are consecutive terms in the sequence increasing?
Plot the points in the table on the graph.
Loading Graph...If the points on the graph were joined, they would form:
a straight line
Aa curved line
B
QUESTION 5
The plotted points represent terms in an arithmetic sequence:
Complete the table of values for the given points.
$n$n $1$1 $2$2 $3$3 $4$4 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
Find the $12$12th term of the sequence.
QUESTION 6
The given table of values represents terms in an arithmetic sequence.
| $n$n | $1$1 | $2$2 | $3$3 | $4$4 |
|---|---|---|---|---|
| $T_n$Tn | $7$7 | $16$16 | $25$25 | $34$34 |
Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
Find the $12$12th term of the sequence.
Applications of arithmetic sequences
We have seen many applications of linear growth or decay when studying linear functions in Chapter 2. Hence, arithmetic sequences apply in many areas of life, including simple interest earnings, straight-line depreciation, monthly rental accumulation and many others. For example, if you are saving money in equal instalments, the cumulative savings at each savings period form an arithmetic sequence. If you are travelling down a highway at a constant speed, the amount of petrol left in the tank, if measured every minute of the trip, forms another arithmetic progression. In fact any time you notice a quantity changing in equal amounts at set time periods, then you can consider that process as being arithmetic.
Worked example
Example 4
Tabitha starts with $\$200$$200 in her piggy bank, the following week she adds $\$25$$25 and then continues to add $\$25$$25 at the start of each successive week. Find a rule to describe $B_n$Bn the balance of her savings at the start of each week and find when her savings will reach $\$450$$450.
Think: The sequence of savings generated is $\$200,\$225,\$250,\$275...$$200,$225,$250,$275... This is arithmetic, so write down the starting value a and common difference and use $t_n=t_1+\left(n-1\right)d$tn=t1+(n−1)d to find a general rule.
Do: $t_1=200$t1=200 and $d=25$d=25 and so our general rule is: $B_n=200+25(n-1)$Bn=200+25(n−1) or equivalently $B_n=175+25n$Bn=175+25n.
To find when the savings reach $\$450$$450, we substitute this into our general rule and solve for $n$n:
| $450$450 | $=$= | $175+25n$175+25n |
| $\therefore25n$∴25n | $=$= | $275$275 |
| $n$n | $=$= | $11$11 |
Hence, at the start of the $11$11th week her savings will have grown to $\$450$$450.
Practice questions
QUESTION 7
A racing car starts the race with $150$150 litres of fuel. From there, it uses fuel at a rate of $5$5 litres per minute.
What is the rate of change?
Fill in the table of values:
Number of minutes passed ($x$x) $0$0 $5$5 $10$10 $15$15 Amount of fuel left in tank in litres ($y$y) $150$150 $\editable{}$ $\editable{}$ $\editable{}$ Write an algebraic equation linking the number of minutes passed ($x$x) and the amount of fuel left in the tank ($y$y).
By rearranging the equation found in part (d), calculate how long it will take for the car to run out of fuel.
QUESTION 8
A car bought at the beginning of 2009 is worth $\$1500$$1500 at the beginning of 2015. The value of the car has depreciated by a constant amount of $\$50$$50 each year since it was purchased.
What was the car purchased for in 2009?
Plot the value of the car, $V_n$Vn, on the graph from 2009 (represented by $n=0$n=0) to 2015 (represented by $n=6$n=6).
Loading Graph...Write an explicit rule for the value of the car after $n$n years.
Give the rule in its expanded form.
Solve for the year $n$n at the end of which the car will be worth half the price it was bought for.