
Exterior Angle Sum and other Calculations
Exterior angle in a triangle
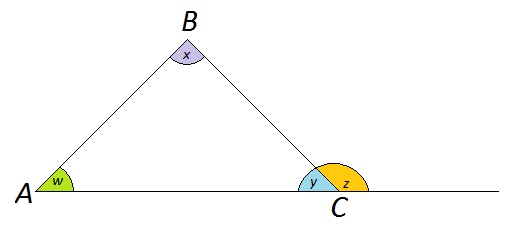
Lets have a look at the triangle image above.
What relationships do we know exist?
We know that $y+z=180$y+z=180, because Adjacent angles on a straight line are supplementary (they add up to $180$180 degrees).
We also know that $w+x+y=180$w+x+y=180 because The angle sum of a triangle is $180$180 degrees.
Since both of these equations sum to $180$180, we know that they are both equal. This means that we have
$y+z=w+x+y$y+z=w+x+y.
Subtracting $y$y from both sides of the equation gives us the result
$z=w+x$z=w+x.
Have a look at where these angles are positioned on the triangle.
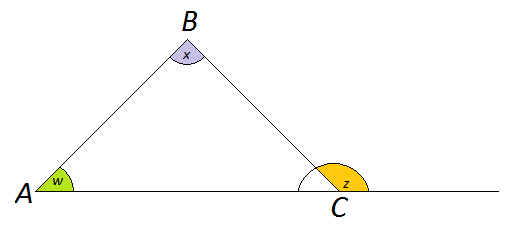
This special relationship is used frequently in solving geometrical problems. We say formally that the: exterior angle of a triangle is equal to the sum of the two opposite interior angles. Can you see how this statement is a description of how the angles are positioned.
This applet can show you how this is the case. Change the size of the triangle and then rotate the angles to fit in the external angle space. Watch this video if you would like to see this interactive in action -
Worked Examples
Question 1
In the diagram, $m$m is the exterior angle of the triangle.

Solve for $m$m using the exterior angle property of a triangle. Give reasons.
Solving problems
When solving angle problems in geometry one of the most important components is the reasoning (or rules) you use to solve the problem. You will mostly be required in geometry problems to not only complete the mathematics associated with calculating angle or side lengths but also to state the reasons you have used. Read through each of these rules and see if you can describe why and draw a picture to represent it.
Geometry Rules with Angles
| Exterior angle of a triangle is equal to the sum of the two opposite interior angles
|
 |
| Angle sum of an n-sided polygon is (n-2)[x]180
|
 |
| Sum of exterior angles of a polygon is 360°
|
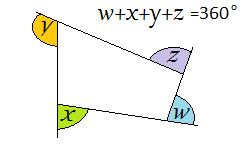 |
| Angle sum of a quadrilateral is 360°
|
 |
| Angles at a point sum to 360° |  |
| Vertically opposite angles are equal |  |
| Adjacent angles forming a right angle are complementary |  |
| Adjacent angles on a straight line are supplementary |  |
A summary of the geometrical properties of triangles can be found here.
A summary of the geometrical properties of quadrilaterals can be found here.