Topics
Measurement
topic badge
Hong Kong
Stage 1 - Stage 3

Volume of Composite Solids II

Lesson
Practice
Lesson

We have already seen how to find the volume of composite solids of varying shapes and sizes.  

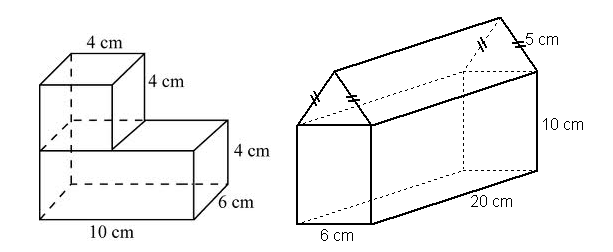
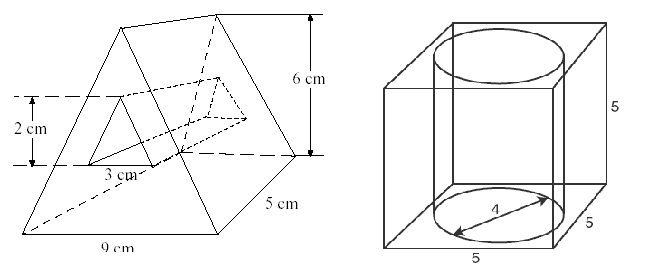
We saw that some are formed by putting together a combination of smaller solids, and that some are formed by removing part of a larger solid. 

Now we can look at many different composite solids and consider them in terms of all the solids we know. 

Volume of Solids Covered So Far

$\text{Volume of Prisms }=\text{Area of Base }\times\text{Height of Prism }$Volume of Prisms =Area of Base ×Height of Prism

$\text{Volume of Cube }=s^3$Volume of Cube =s3

$\text{Volume of Rectangular Prism }=lwh$Volume of Rectangular Prism =lwh

$\text{Volume of Cylinder }=\pi r^2h$Volume of Cylinder =πr2h

$\text{Volume of Right Pyramid }=\frac{1}{3}\times\text{Base Area}\times\text{Height of Pyramid}$Volume of Right Pyramid =13​×Base Area×Height of Pyramid

$\text{Volume of Right Cone }=\frac{1}{3}\pi r^2h$Volume of Right Cone =13​πr2h

$\text{Volume of Sphere }=\frac{4}{3}\pi r^3$Volume of Sphere =43​πr3

Worked Examples

Question 1

Find the volume of the figure shown, correct to two decimal places.

A three-dimensional composite figure which is a combination of a rectangular prism and a half-cylinder. The length of the rectangular prism  is labeled as $10$10 m. The base of the rectangular prism has congruent sides as indicated by the single tick mark on each side, with the bottom side labeled $4$4 m.  The flat surface of the half cylinder coincides with the top face of the rectangular prism such that its height directly overlaps the rectangle's length. The diameter of the semicircular base of the cylinder is the top side of the base of the rectangular prism. 

Question 2

Find the volume of the composite figure shown, correct to two decimal places.

 

What is Mathspace

About Mathspace