16.01 Discrete probability distributions
Discrete and continuous random variables
Now that we know what a Discrete Random Variable (DRV) is, we want to compare this with what constitutes a Continuous Random Variable (CRV).
As you'll notice from the names, the only difference is the word Discrete which has been changed to Continuous. And that's the only difference in the definitions too!
Defining a Continuous Random Variable
- Firstly, the outcomes of the situation or the experiment must occur over an interval of space or time.
- Remember that continuous data is numerical and is data that has been measured.
- For example, if you were to measure the heights of students in a particular grade, the possible outcomes would exist over a range of heights, let's say between $155$155 cm and $175$175 cm. This unit of length is a unit in space.
- The outcomes must occur at random.
- In an experiment or situation all the outcomes must occur randomly.
- For example, the time you must wait at an ATM is occurs randomly. Time is a unit of measurement and is continuous.
- The outcomes must vary.
- There needs to be more than one outcome and thus the outcomes vary.
- For a CRV, the outcomes will vary because they will always exist over an interval. In fact, when we're observing data or an experiment that is measured, we cannot examine one single outcome. This will be explained later on when we delve into CRVs in more detail.
Discrete versus continuous random variables
When determining whether you're looking at a DRV or a CRV, you firstly need to make sure that the experiment or situation is random and varies.
You then need to consider whether the outcomes consist of discrete or continuous values.
Remember that what you're asking yourself is whether the outcomes are counted or measured.
Worked Example
Question 1
The mass of each egg in an $18$18-pack carton of Extra Large Eggs ranges in weight from $67$67 g to $72$72 g.
(a) Can the weight of the eggs in the carton be modeled by a probability distribution?
Think: We need to check firstly that the outcomes (the weights of the eggs) are random and vary. We then need to think about what sort of data we're dealing with.
Do: The weights certainly vary because we're told they range between $67$67 g and $72$72 g. We know the eggs are randomly assigned to each space in the egg carton and we'd choose one at random.
We also know that we'd need to measure the weight of each egg, not count it.
Therefore we can say that this situation is modeled by a continuous random variable.
(b) Which of the following graphs best models the shape of this continuous probability distribution?

Think: Because we don't have a lot of experience with CRVs, we'll have to really think about what we expect to happen in this real-life situation. You have to use some common sense!
Do: Let's take a look at what each graph is telling us.
- The first graph, in the top left, is showing that the probability of each outcome is uniform.
- The second graph, in the top right, is showing us that the probability at the lower end of the range of outcomes is much higher than the probability at the lower end of the range of outcomes.
- The third graph, in the bottom left, is showing us that probability of the range of outcomes is positively skewed.
- The fourth graph, in the bottom right, is showing us that the probability of the range of outcomes is symmetrical and the greatest probability occurs at the middle of the range.
When we think about the weights of the eggs in a carton that is advertised as containing Extra Large Eggs, we should expect that the majority of the eggs will be the same size and weight and that there's a lower chance that an egg will be at the lower or higher range of weights. So the mean weight should have the greatest probability. We are therefore looking at the fourth graph as our answer.
Practice questions
Question 2
At the beginning of the year, a teacher seats his students alphabetically to learn their names quickly.
Can we use a probability distribution to model where a particular child will sit in the class?
No
AYes, a discrete probability distribution
BYes, a continuous probability distribution
CWhich of the following explains why a probability distribution doesn’t exist for this situation?
The outcomes are not random.
AThe outcomes are not variable.
B
Question 3
A manager randomly selects three of his staff to attend a leadership conference. He randomly selects people from his Sales team and his Development team.
Can the number of Sales people chosen be modeled by a probability distribution?
Yes, a continuous probability distribution
AYes, a discrete probability distribution
BNo
CGiven that there are four people on the Sales team, list all of the possible outcomes of this distribution.
Give all answers on the same line separated by commas.
Question 4
The traffic signal at a particular pedestrian crossing remains red for $3$3 minutes.
Frank arrives at the pedestrian crossing to find that the light is currently red.
Can the length of time Frank will be waiting for the light to turn green be modeled by a probability distribution?
Yes, by a discrete probability distribution
ANo
BYes, by a continuous probability distribution
CWhich of the following graphs best models the shape of this continuous probability distribution?
Here $t$t represents the time Frank could wait at the light and $P\left(t\right)$P(t) represents the probability that Frank will wait for time $t$t.
Loading Graph...ALoading Graph...BLoading Graph...CLoading Graph...D
Question 5
The mass of each egg in an $12$12-pack carton of Extra Large Eggs ranges in weight from $66$66g to $72$72g.
Can the mass of the eggs in the carton be modeled by a probability distribution?
No
AYes, by a continuous probability distribution
BYes, by a discrete probability distribution
CWhich of the following graphs best models the shape of this continuous probability distribution?
Loading Graph...ALoading Graph...BLoading Graph...CLoading Graph...D
As we have seen, a Discrete Random Variable, or DRV for short, is when each outcome in a random experiment is assigned a number.
A Continuous Random Variable, or CRV for short, is when we examine the outcomes over an interval for a random experiment.
An easy way to think about it is this: we count the outcomes for a DRV and we measure the outcomes for a CRV.
Now that we know the difference between a DRV and CRV, we want to take a closer look at DRVs, and in particular, we want to look at the distribution of the probabilities.
The Probability Distribution of a Discrete Random Variable
For a DRV, each outcome is assigned a probability.
For example, let's say we toss a coin twice and we're interested in how many tails we see.
Firstly we can define our DRV. Let $X$X be the number of tails in a two coin toss.
We then know that $X$X can take on the values of $0$0, $1$1 or$2$2.
The probability distribution for X will show us the probabilities for each of these outcomes. An easy way to do that for this example is to look at a tree diagram.

We'll now examine our tree diagram and tabulate the probabilities.
| $x$x | 0 | 1 | 2 |
|---|---|---|---|
| $P(X=x)$P(X=x) | $\frac{1}{4}$14 | $\frac{2}{4}$24 | $\frac{1}{4}$14 |
What we've just created is the probability distribution for the random variable $X$X.
How can we represent a probability distribution for a DRV?
There are a few ways we represent a probability distribution for a DRV.
- We can create a table of values. This is the most common method.
- We can create a function. You will see this very soon.
- We can draw a graph.
The graph of a probability distribution for a DRV.
The graph of a probability distribution of a DRV is a probability histogram.
Either of these two graphs can be used to represent the DRV $X$Xthat we were discussing earlier.

Uniform vs non-uniform DRVs
A uniform DRV is when all outcomes of the experiment are equally likely.
For example, when you roll a dice once, the probability of rolling a $1$1,$2$2, $3$3, $4$4,$5$5 or $6$6 are all equally likely, or uniform.
The probability histogram below of one roll of the dice shows this uniform shape nicely.
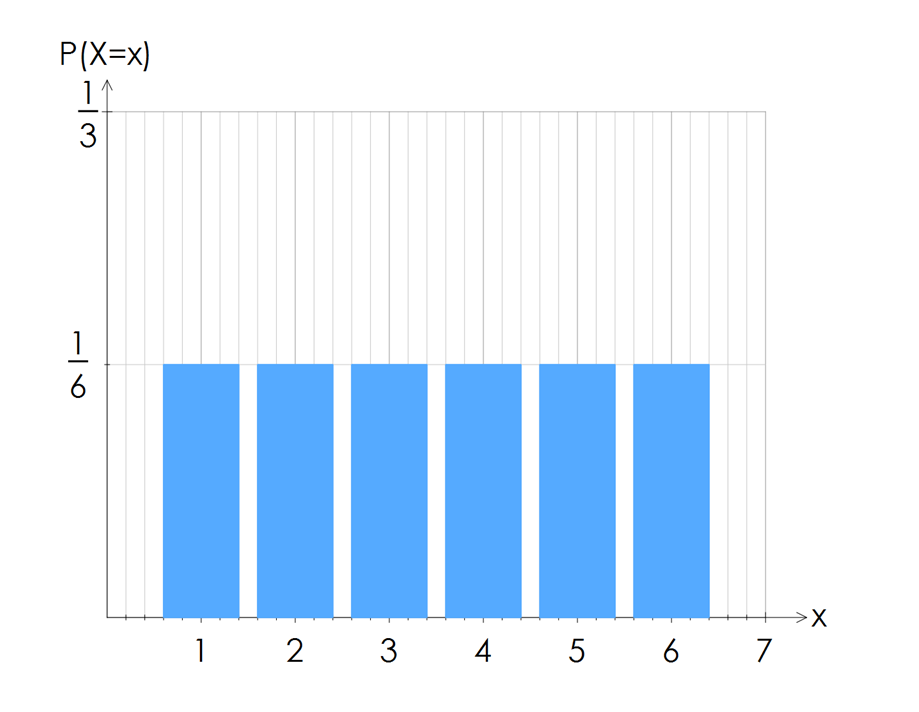
A non-uniform DRV is when not all outcomes are equally likely. This is the vast majority of DRVs that we'll see.
Properties of a probability distribution of a DRV
If we examine what appears to be a probability distribution, either in a table, a graph or a function, we need to make sure each of the following three properties apply:
- All outcomes are numerical - no categorical data
- The sum of all the probabilities equals $1$1 - no missing outcomes
- All the outcomes have non-negative probabilities - negative probability doesn't make any sense
Worked examples
Question 6
Is the following a probability distribution?
| $x$x | $2$2 | $4$4 | $6$6 | $8$8 |
|---|---|---|---|---|
| $p\left(x\right)$p(x) | $0.2$0.2 | $0.4$0.4 | $0.6$0.6 | $0.8$0.8 |
No
AYes
B
Question 7
Consider the following table.
| $x$x | $2$2 | $4$4 | $5$5 | $6$6 | $7$7 |
|---|---|---|---|---|---|
| $P$P$($($X=x$X=x$)$) | $0.1$0.1 | $0.25$0.25 | $0.3$0.3 | $0.15$0.15 | $0.2$0.2 |
Identify which conditions for a discrete probability distribution are evident in the table.
Select all that apply.
$X$X is discrete numerical
A$\Sigma P\left(x\right)=1$ΣP(x)=1
B$0\le P$0≤P$\left(x\right)\le1$(x)≤1
CNone of the conditions
DTherefore, does this table represent a discrete probability distribution?
No
AYes
B
Question 8
Consider the following graph.
Identify which conditions for a discrete probability distribution are evident in the graph.
Select all that apply.
$X$X is discrete numerical
A$\Sigma P\left(x\right)=1$ΣP(x)=1
B$0\le P$0≤P$\left(x\right)\le1$(x)≤1
CNone of the conditions
DTherefore, does this graph represent a discrete probability distribution?
Yes
ANo
B
Constructing a discrete probability distribution
When we are required to construct our own discrete probability distribution, there are a number of things that this could mean.
We could be asked to:
- Read and interpret an experiment and represent the probability distribution as a table
- Read and interpret an experiment and represent the probability distribution as a function
In this section where we're mainly dealing with general discrete random variables, we'll mostly be constructing tables to represent our distributions.
How to construct a discrete probability distribution
- Define exactly what your random variable $X$X represents.
Note: You can use any capital letter for your random variable, but most often we use $X$X
- Consider how many possible outcomes $X$X can take.
- Devise a method for calculating the probabilities for each outcome.
Note: The main methods you will use here is either constructing a sample space (the most common being a tree diagram or a table) or using counting techniques (combinations)
- Calculate your probabilities and represent them in a table.
You have now created an individual probability distribution for your random variable!
Worked examples
Question 9
A fair standard dice is thrown and the number of dots on the uppermost face is noted.
Let $X$X be the number of dots on the uppermost face.
(a) Construct the probability distribution for $X$X.
Think: In this example the random variable has already been defined for us. All we need to do is determine the number of possible outcomes and then work out their associated probabilities.
Do: The outcomes for $X$X are $1,2,3,4,5$1,2,3,4,5 and $6$6 since we're talking about rolling a standard dice. We also know the probabilities for each are $\frac{1}{6}$16 since each outcome is equally likely.
Now we construct a table of values.
| $x$x | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 | $6$6 |
|---|---|---|---|---|---|---|
| $P(X=x)$P(X=x) | $\frac{1}{6}$16 | $\frac{1}{6}$16 | $\frac{1}{6}$16 | $\frac{1}{6}$16 | $\frac{1}{6}$16 | $\frac{1}{6}$16 |
And there we have our probability distribution.
(b) State the type of distribution which $X$X represents.
Think: Our discrete distributions can either be uniform or non - uniform. Later on you'll learn about specific types of non-uniform discrete random variables.
Do: Since all outcomes have the same probability, this distribution is a uniform distribution.
Practice questions
QUESTION 10
An unfair coin is tossed. The chance of tails facing upwards after the toss is $30%$30%.
Determine the probability of the coin landing tails up for the first time on the third toss.
Determine the probability of the coin landing tails up for the first time on the fourth toss.
Determine the probability that it takes four tosses of the coin before you see a tail on the fifth toss.
Let $N$N be the number of tosses of the coin it takes before you see a tail on the next toss.
Define the probability density function for $N$N.
QUESTION 11
A pencil case contains $9$9 blue pens and $5$5 green pens. $4$4 pens are drawn randomly from the pencil case, one at a time, each being replaced before the next one is drawn.
What is the probability of drawing one blue pen from the pencil case?
Fully simplify your answer.
What is the probability of drawing three blue pen from the pencil case?
Fully simplify your answer.
Let $X$X be the number of blue pens drawn. Complete the probability distribution table.
Fully simplify your answers.
$x$x $0$0 $1$1 $2$2 $3$3 $4$4 $P\left(X=x\right)$P(X=x) $\frac{625}{38416}$62538416 $\editable{}$ $\frac{6075}{19208}$607519208 $\editable{}$ $\editable{}$
Discrete probability density functions
As we've seen, we can represent a probability distribution for a discrete random variable (DRV) with a table of probabilities or a graph.
We can sometimes also represent a probability distribution for a DRV with what we call a probability density function or a probability distribution function. In other words, we can write an algebraic equation that will generate the probability for each possible outcome.
For example, if we consider the simple example of all the possible outcomes when we roll a normal six-sided dice, we would obtain the following probability distribution function:
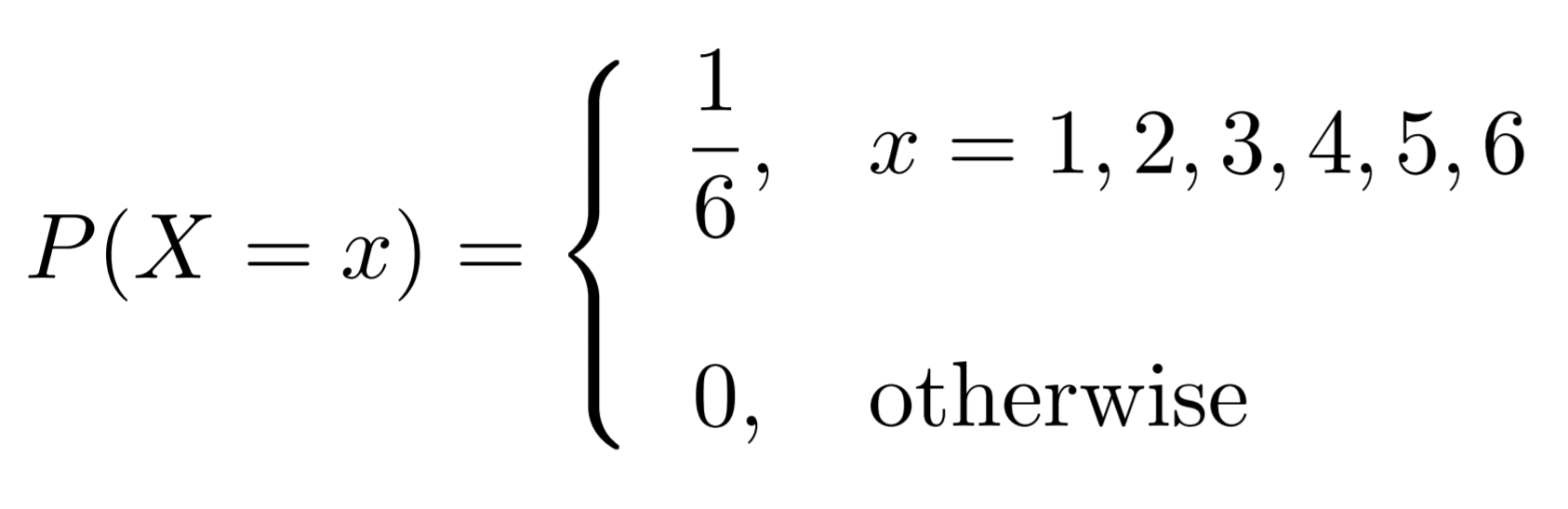
Properties of the distribution of a DRV
It's so important to remember these three properties, that we'll put them here again:
- All outcomes are numerical.
- The sum of all the probabilities equals $1$1.
- None of the probabilities can be zero.
If you are required to write your own probability density function from some information given, then make sure you remember to write all the possible domain values (that is, all the possible outcomes) for which the function conforms to the properties stated above.
Worked Examples
Question 12
The probability function for a uniform discrete random variable is given below:
| $P$P$($($X=x$X=x$)$) | $=$= |  |
$k$k; $x=1,2,3,4$x=1,2,3,4 |
| $0$0, for all other values of $x$x |
Determine the value of $k$k.
Calculate $P$P$($($X<3$X<3$)$).
Calculate $P$P$($($X\ge2$X≥2 $|$| $X<4$X<4$)$).
Determine $m$m such that $P$P$($($X\ge m$X≥m$)=0.75$)=0.75.
Question 13
The probability function for a discrete random variable is given by:
| $P$P$($($X=x$X=x$)$) | $=$= |  |
$k\left(9-x\right)$k(9−x); $x=4,5,6,7,8$x=4,5,6,7,8 |
| $0$0, for all other values of $x$x |
Determine the exact value of $k$k.
Hence complete the table of values.
$x$x $4$4 $5$5 $6$6 $7$7 $8$8 $P$P$($($X=x$X=x$)$) $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Calculate $P$P$($($X<7$X<7$)$).
Calculate $P$P$($($X\ge6$X≥6$)$).
Calculate $P$P$($($X<6$X<6$\cup$∪$X>7$X>7$)$).
Calculate $P$P$($($X\ge5$X≥5$|$|$X\le7$X≤7$)$).
Question 14
The probability function for a discrete random variable is given by:
| $P$P$($($X=x$X=x$)$) | $=$= |  |
$\nCr{5}{x}$5Cx$\left(0.6\right)^x$(0.6)x$\left(0.4\right)^{5-x}$(0.4)5−x; $x=0,1,2,3,4,5$x=0,1,2,3,4,5 |
| $0$0, for all other values of $x$x |
Complete the table of values.
Give each value to five decimal places.
$x$x $0$0 $1$1 $2$2 $3$3 $4$4 $5$5 $P(X=x)$P(X=x) $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Which of the following describes the shape of the probability distribution?
negatively skewed
Apositively skewed
Bsymmetrical
CCalculate $P$P$($($X>3$X>3$)$).
Give your answer to five decimal places.
Calculate $P$P$($($X>0$X>0$)$).
Give your answer to five decimal places.
Calculate $P$P$($($X\le3$X≤3$|$|$X>0$X>0$)$).
Give your answer to five decimal places.
Measures of center of discrete random distribution
When analyzing the outcomes and probabilities of a Discrete Random Variable, we become interested in the expected value of the distribution.
Based on the probabilities, the expected value is which outcome we expect to occur within the given experiment.
The expected value, denoted $E(X)$E(X), can also be thought of as the mean of the distribution, and is in fact calculated like a weighted average.
Worked examples
Question 15
Consider the probability distribution of a DRV given in the table below.
| $x$x | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 |
|---|---|---|---|---|---|
| $P(X=x)$P(X=x) | $0.2$0.2 | $0.15$0.15 | $0.4$0.4 | $0.1$0.1 | $0.15$0.15 |
To calculate the mean, we multiply each outcome by its probability. The probability represents the weighting for each outcome occurring.
$E\left(x\right)=1\times0.2+2\times0.15+3\times0.4+4\times0.1+5\times0.15$E(x)=1×0.2+2×0.15+3×0.4+4×0.1+5×0.15
$E\left(x\right)=2.85$E(x)=2.85
Let's consider what this means. Clearly we're not really "expecting" an outcome of $2.85$2.85. All possible outcomes are discrete and are listed in the table.
It's just like when they say the average number of children per family is $2.3$2.3. No family will have $0.3$0.3 of a child! But the mean value gives us an idea about how many children we can expect to see in a family; somewhere between two and three.
So in our experiment we don't expect to get $2.85$2.85, but in the long term we expect the average of all our occurrences to come to $2.85$2.85.
Similarly, the expected value is not to be confused with the most likely outcome. In our distribution above, the most likely outcome is $3$3 since $P(X=3)$P(X=3) has the greatest probability of $0.4$0.4.
Let's take a look at one more example to see another way using the expected value can crop up.
Question 16
Consider the probability distribution of a DRV given in the table below, where $E(X)=3.05$E(X)=3.05
| $x$x | $0$0 | $1$1 | $3$3 | $5$5 | $6$6 |
|---|---|---|---|---|---|
| $P(X=x)$P(X=x) | $0.3$0.3 | $a$a | $0.1$0.1 | $b$b | $0.15$0.15 |
Determine the values of $a$a and $b$b.
Since we have two unknowns we need two equations to use in solving for $a$a and $b$b.
We are told that the table represents a DRV, so we know all the probabilities must add to $1$1. So our first equation is:
$0.3+a+0.1+b+0.15=1$0.3+a+0.1+b+0.15=1
Simplifying gives us:
$a+b=0.45$a+b=0.45
Using the expected value we can form another equation.
$0\times0.3+1\times a+3\times0.1+5\times b+6\times0.15=3.05$0×0.3+1×a+3×0.1+5×b+6×0.15=3.05
Simplifying gives us:
$a+5b=1.85$a+5b=1.85
Solving using the elimination method or using the solving functionality of your calculator gives us:
$4b=1.4$4b=1.4
$b=0.35$b=0.35 and $a=0.1$a=0.1
Practice questions
Question 17
Consider the probability density function defined by:
| $P$P$($($X=x$X=x$)$) | $=$= |  |
$\frac{x}{25}$x25; $x=3$x=3, $4$4, $5$5, $6$6, $7$7 |
| $0$0, otherwise |
Does this probability density function represent the distribution for a discrete random variable?
Yes
ANo
BHence complete the table of values for this probability distribution.
$x$x $3$3 $4$4 $5$5 $6$6 $7$7 $P$P$($($X=x$X=x$)$) $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Now calculate the expected value of the distribution.
Question 18
Examine the graph of the probability distribution below.
Calculate the expected value of the discrete probability distribution.
Is the median of this distribution higher, lower or equal to the mean?
equal
Ahigher
Blower
CWhat is the reason for your answer in part b of this question?
The graph is negatively skewed.
AThe graph is positively skewed.
BThe graph is symmetrical.
C
Measures of variability of discrete random distribution
Just as we can calculate the mean for the probability distribution of a Discrete Random Variable, we can also calculate the variance and standard deviation.
We calculate the variance in the exact same way we calculate the variance of a set of data.
The only difference is including the weightings, or the probabilities, into our calculations.

As you can see, there are two versions of the Variance formula. Question $19$19 demonstrates the first formula, and question $20$20 demonstrates the second.
Worked examples
Question 19
Consider the table.
| $x$x | $0$0 | $1$1 | $2$2 | $3$3 | $4$4 |
|---|---|---|---|---|---|
| $P$P$($($X=x$X=x$)$) | $0.12$0.12 | $0.15$0.15 | $0.22$0.22 | $0.23$0.23 | $0.28$0.28 |
Does the table represent a discrete probability distribution?
Yes
ANo
BCalculate $E\left(X\right)$E(X).
Calculate the variance of $X$X.
Hence calculate the standard deviation.
Give your answer to two decimal places.
Question 20
Let's use the same probability distribution from our previous chapter as an example of how to calculate the variance of a probability distribution.
Consider the probability distribution of a DRV given in the table below.
| $x$x | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 |
|---|---|---|---|---|---|
| $P(X=x)$P(X=x) | $0.2$0.2 | $0.15$0.15 | $0.4$0.4 | $0.1$0.1 | $0.15$0.15 |
Calculate the variance and standard deviation of the distribution.
We already know from last time that the mean, or expected value is $E(X)=2.85$E(X)=2.85
Calculating the variance we get:
$Var\left(X\right)=\left(1^2\times0.2+2^2\times0.15+3^2\times0.4+4^2\times0.1+5^2\times0.15\right)-2.85^2$Var(X)=(12×0.2+22×0.15+32×0.4+42×0.1+52×0.15)−2.852
$Var\left(X\right)=1.6275$Var(X)=1.6275
To calculate the standard deviation we simply find the square root of the variance.
$\sigma\left(X\right)=\sqrt{1.6275}$σ(X)=√1.6275
$\sigma\left(X\right)=1.2757$σ(X)=1.2757
Practice questions
Question 21
Consider the graph drawn below of a discrete probability distribution.
Calculate the expected value of this distribution.
Would you expect the median to be greater than, less than or equal to the expected value of this distribution?
less than
Agreater than
Bequal to
CCalculate the variance of this distribution.
Hence, calculate the standard deviation.
Give your answer to one decimal place.
Would you expect the standard deviation of the distribution drawn below to be greater than, less than or equal to the standard deviation of our original distribution?
Loading Graph...less than
Aequal to
Bgreater than
C
Question 22
Consider the probability density function given below:
| $p\left(x\right)$p(x) | $=$= |  |
$\frac{x}{10}$x10; $x=1$x=1, $2$2, $3$3, $4$4 |
| $0$0, otherwise |
Complete the table of values for this probability distribution.
$x$x $1$1 $2$2 $3$3 $4$4 $P$P$($($X=x$X=x$)$) $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Hence calculate the mean of the distribution.
Calculate the standard deviation of the distribution.
Mean and variance of linear combinations of DRV
What happens to the mean and variance of a probability distribution when all outcomes experience a change in scale and/or origin?
Let's first experiment with some data.
Change of scale and origin on univariate data
Let's take the heights of $10$10 students in a class, recorded in meters.
$1.64$1.64 $1.67$1.67 $1.70$1.70 $1.71$1.71 $1.63$1.63 $1.55$1.55 $1.60$1.60 $1.71$1.71 $1.69$1.69 $1.72$1.72
The population mean and standard deviation for this data set is mean = $1.662$1.662 and standard deviation = $0.053$0.053
What would happen to the mean and standard deviation if we had recorded these results in centimeters instead of meters?
To investigate this we need to convert all the measurements to cm, and to do this we need to multiply each score by $100$100. This is called a change of scale.
We can calculate that the mean = $166.2$166.2 and the standard deviation = $5.3$5.3
So what's happened to the mean and standard deviation? They've both been multiplied by the same scale factor as the data. That is, they've also been multiplied by $100$100.
What if instead, we decided we needed to subtract $2$2 cm from each height (that is, $0.02$0.02 m) to account for the height of the heel of school shoes?
Once again, you will first need to subtract $0.02$0.02 from each original data point and recalculate the mean and standard deviation. This is called a change of origin.
We can calculate that mean = $1.642$1.642 and the standard deviation = $0.053$0.053
So what's happened to the mean and standard deviation? Only the mean has decreased by $0.02$0.02, the standard deviation has stayed the same.
This makes complete sense. If you add or subtract an amount from all data points you will not change the spread of the data, just the location of the mean, and so the standard deviation won't change.
Change of scale and origin on a probability distribution
The same effects as we saw above occur if we change the scale and/or origin of the outcomes in a probability distribution.
Let's say have the probability distribution for $X$X whose outcomes undergo the transformations $aX+b$aX+b, then:
$E(aX+b)=aE(X)+b$E(aX+b)=aE(X)+b
$Var(aX+b)=a^2Var(X)$Var(aX+b)=a2Var(X)
Note that we multiply the variance by $a^2$a2, not $a$a, since this is variance and not standard deviation.
Worked Example
Question 23
Consider the probability distribution for a discrete random variable given in the table below.
| $x$x | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 |
|---|---|---|---|---|---|
| $P(X=x)$P(X=x) | $0.2$0.2 | $0.15$0.15 | $0.4$0.4 | $0.1$0.1 | $0.15$0.15 |
Calculate:
(a) $E(2X-4)$E(2X−4)
(b) $Var(2X-4)$Var(2X−4)
We saw in the last few chapters that $E(X)=2.85$E(X)=2.85 and $Var(X)=1.6275$Var(X)=1.6275
To calculate the new expected value under a change of scale of $2$2 and a change of origin of $-4$−4, we apply both of these to our original expected value, since the mean is affected by both.
So $E\left(2X-4\right)=2\times2.85-4$E(2X−4)=2×2.85−4
$E\left(2X-4\right)=1.7$E(2X−4)=1.7
To calculate the new variance, it will only be affected by the change of scale, not the change of origin.
So $Var\left(2X-4\right)=2^2\times1.6275$Var(2X−4)=22×1.6275
$Var\left(2X-4\right)=6.51$Var(2X−4)=6.51
Practice questions
Question 24
The expected value of a discrete random variable is $E\left(X\right)=4.3$E(X)=4.3
Calculate $2E\left(X\right)$2E(X).
Calculate $E\left(2X\right)$E(2X).
Calculate $E\left(X-1\right)$E(X−1).
Calculate $E\left(4X+1\right)$E(4X+1).
Solve for the value of $n$n such that $E\left(nX+3\right)=11.6$E(nX+3)=11.6.
Question 25
The table below represents the distribution of a discrete random variable, where $E\left(X\right)$E(X) is the expected value, $V\left(X\right)$V(X) is the variance and $S\left(X\right)$S(X) is the standard deviation.
| $x$x | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 |
|---|---|---|---|---|---|
| $P$P$($($X=x$X=x$)$) | $0.5$0.5 | $m$m | $0.15$0.15 | $n$n | $0.05$0.05 |
Express $m$m in terms of $n$n.
Given that $E\left(X^2\right)=5.5$E(X2)=5.5, solve for the value of $n$n.
Hence find $m$m.
Calculate $E\left(X\right)$E(X).
Calculate $V\left(X\right)$V(X).
Calculate $E\left(5X+7\right)$E(5X+7).
Calculate $S\left(4-X\right)$S(4−X).
Give your answer to one decimal place.
Question 26
Spacemaths is selling an online eBook for $\$20$$20 per student.
The table below shows the probabilities associated with the number of students purchasing the product and the associated costs for the company.
| Number of students purchasing | Costs | Probability |
|---|---|---|
| $50000$50000 | $\$70000$$70000 | $0.2$0.2 |
| $100000$100000 | $\$100000$$100000 | $0.1$0.1 |
| $200000$200000 | $\$120000$$120000 | $0.4$0.4 |
| $500000$500000 | $\$150000$$150000 | $0.3$0.3 |
Calculate the expected number of students purchasing the product.
Hence calculate the expected revenue.
Calculate the expected cost for Spacemaths.
Hence calculate the expected profit for Spacemaths.
If students were offered a $25%$25% discount, calculate the expected profit for Spacemaths. Assume the probabilities are the same.