11.01 Angles of polygons
Interior angles of polygons
Interior angles of polygons are all the angles that are inside a shape. Depending on whether we know the number of sides in or the angle sum of a polygon, we can use the information to find:
- the angle sum of the interior angles of the polygon
- the size of each angle in the polygon
- the number of sides in the polygon, or
- the type of polygon.
Exploration
We've already learned that the interior angle sum of a triangle is $180^\circ$180° with our Triangle Sum theorem.
Let's consider the following polygon, in particular a pentagon, that has been divided up into triangles by drawing lines from one vertex to each of the other vertices:

So, the angle sum of this pentagon is then:
| Interior Angle Sum | $=$= | $\left(a+f+i\right)+b+\left(c+d\right)+\left(e+g\right)+h$(a+f+i)+b+(c+d)+(e+g)+h |
Definition of interior angle sum |
| $=$= | $\left(a+b+c\right)+\left(d+e+f\right)+\left(g+h+i\right)$(a+b+c)+(d+e+f)+(g+h+i) |
Commutative property |
|
| $=$= | $180^\circ+180^\circ+180^\circ$180°+180°+180° |
Triangle Sum theorem |
|
| $=$= | $3\left(180^\circ\right)$3(180°) |
Definition of multiplication |
|
| $=$= | $540^\circ$540° |
Addition |
Notice that the pentagon has $5$5 sides and it makes $3$3 triangles.
Use this GeoGebra applet to explore the general case of how many triangles would be in an $n$n-sided polygon.
The number of triangles produced by drawing lines from one vertex to the others in a polygon, will always be two less than the number of sides in that polygon. This pattern is consistent for all polygons.
This interactive will show you different interior angle sums for different polygons. You can also see how many triangles fit into it.
The sum of the measures of the interior angles of a convex $n$n-gon is $(n-2)\cdot180^\circ$(n−2)·180°.
$S=m\angle1+m\angle2+...+m\angle n=(n-2)\cdot180^\circ$S=m∠1+m∠2+...+m∠n=(n−2)·180°
Following from this we can also see that for a regular polygon, each interior angle would have a measure of:
$\frac{(n-2)\cdot180^\circ}{n}$(n−2)·180°n
As mentioned above, we can use this theorem to solve many different types of problems.
Exterior angles in a polygon
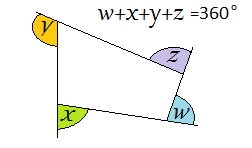
Why is the sum of the exterior angles of any convex polygon always 360°?
Why is the result the same for a 3-sided polygon (i.e. a triangle) as for a 20-sided polygon?
To see why, imagine you are driving a car around this polygonal track. What is the total of the angles you turn when doing 1 complete lap. These angles are the external (exterior) angles of the polygon. What is the sum?
Make sure you keep the polygon convex (no concave structures). See here to remind yourself the difference between convex and concave.
Watch this video if you would like to see this interactive in action -
The sum of the exterior angles of a convex polygon is always $360^\circ$360°.
Following from this, each exterior angle in an n-sided regular polygon would have a measure of $\frac{360^\circ}{n}$360°n.
Worked Examples
Question 1
Dave Claims to have drawn a regular polygon with interior angles equal to $100^\circ$100°. Is this possible, if so find $n$n, the number of sides of such a polygon.
Think: If we consider that each angle is $100^\circ$100° and that there are $n$n interior angles, this means that the sum of the interior angles is $\left(100n\right)$(100n). We can then use the interior angle sum theorem to solve for $n$n.
Do:
| Sum of interior angles | $=$= | $\left(n-2\right)\times180^\circ$(n−2)×180° |
Polygon interior angle sum theorem |
| $100n$100n | $=$= | $\left(n-2\right)\times180$(n−2)×180 |
Filling in given information |
| $100n$100n | $=$= | $180n-360$180n−360 |
Distributive property |
| $180n-100n$180n−100n | $=$= | $360$360 |
Subtract $100n$100n and add $360$360 to both sides |
| $80n$80n | $=$= | $360$360 |
Combine Like Terms |
| $n$n | $=$= | $\frac{360}{80}$36080 |
Divide both sides by $80$80 |
| $n$n | $=$= | $4.5$4.5 |
Simplify |
Reflect: Side number must be an integer value, so $4.5$4.5 is not a valid answer. Dave must have measured incorrectly as it is not possible to make a regular polygon with each interior angle measuring $100^\circ$100°.
Practice questions
Question 2
Consider the quadrilateral in the adjacent figure.

Find the value of the angle marked $y$y.
Find the value of the angle marked $x$x.
Complete:
The sum of the interior angles of a quadrilateral is $\editable{}$°.
Question 3
Find the value of the variable in the following figure.

Question 4
Neil claims to have drawn a regular polygon with each exterior angle equal to $72^\circ$72°.
Find $n$n, the number of sides of such a polygon.
Hence what type is this shape ?
Hexagon
ANonagon
BOctagon
CThis shape cannot exist
DHeptagon
EPentagon
F